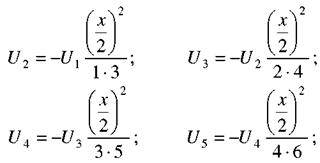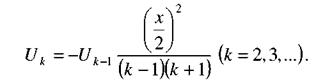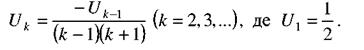Слід знати, що ітераційним називають обчислювальний процес (цикл), кількість повторень якого наперед невідоме. Умовою закінчення обчислення є досягнення заданої точності, котра характеризується величиною похибки ε. Звичайно ε - мале додатне число.
До ітераційних циклів приводить використання методів послідовних наближень. Суть таких методів складає багаторазове обчислення однієї й тієї ж ітераційної формули, причому результат попереднього обчислення є вихідним для наступного обчислення.
Методи послідовних наближень використовуються при обчисленні рядів із заданою точністю, при находженні коренів алгебраїчних і трансцендентних рівнянь виду f(x) = 0іт.д.
2 Приклад обчислення значення функції БесселяJ2 (x)
Скласти блок-схему алгоритму та програму для обчислення значення функції Бесселя J2(x) з точністю ε = 10-3, коли x = 2, скориставшись формулою

Ця задача на організацію ітераційного обчислювального процесу, до якого зводиться розрахунок із заданою точністю ε рядів з нескінченною верхньою границею. При цьому використовується відоме положення, що процес обчислення суми знакозамінних і деяких знакопостійних рядів може бути припиненим, як тільки черговий обчислений член ряду буде за модулем менше заданої дозволеної похибки ε.
Вихідний ряд

перепишемо у вигляді рекурентного співвідношення. Для цього зазначимо, що нехай 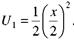 Тоді
Тоді
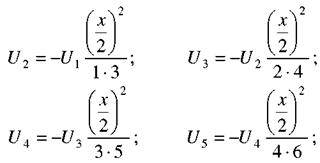
і так далі. З цього слідує, що довільний член ряду може бути обчислений за рекурентною формулою
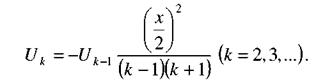
Так як х = 2, то формули суттєво спрощуються
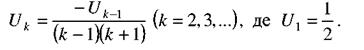




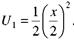 Тоді
Тоді