Це арифметичні пристрої, що призначені для порівняння двох чисел, що подані у двійковому (двійково-десятковому) коді.
Найпростіший компаратор виявляє лише факт рівності або нерівності двох поданих на його входи n- розрядних чисел (операндів) А і В, і формує на виході однобітовий сигнал рівності (1) або нерівності (0) цих чисел.
Рівність, зокрема, двох операндівaі bвизначається логічною операцією однозначності, або еквівалентності
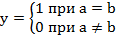 , (1)
, (1)
тобто логічною операцією ВИЙНЯТКОВО АБО-НЕ, яка реалізується суматором-інвертором за mod2.
Покажемо це:
Операція рівнозначності (1) записується як
 .
.
Звідси 
a
Y - однорозрядний суматор рівності.
b
Реалізація його доволі просто здійснюється у довільному базисі.
Порозрядну рівність n- розрядних операндів найпростіше реалізувати за допомогою суматорів-інверторів за mod2 і кон’юнкторів.Такий компаратор рівностей порівнює окремі розряди n-розрядних чисел за формулою:
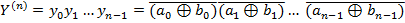
Реалізація цієї функції:
a0 Y0
b0
a1 Y1 Y
b1
an-1 Yn-1
bn-1
Аналогічний результат отримаємо і при синтезі компаратора у базисі суматорів за mod2 і диз’юнкторів. Якщо застосувати закон дуальності, то вихідна функція такого компаратора описується виразом:
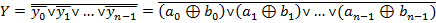
Компаратори порівняння n-розрядних чисел можна будувати за двома принципами:
1. Логічним
2. Арифметичним.
Логічний принцип базується на синтезі за таблицею істинності.
Порівняння n-розряднихоперандів А і В є більш складною процедурою- воно визначається системою нерівностей, що складається з двох функцій:
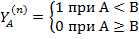 ;
; 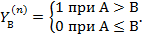
Таблиця істинності компаратора двох однорозрядних чисел має вигляд:
| a b
| YaYb
|
| 0 0
0 1
1 0
1 1
| 0 0
1 0
0 1
0 0
|
Звідси: 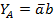 – заборона по a
– заборона по a
 – заборона поb.
– заборона поb.
Схема приведена на рис 5.
a Ya
b
Yb
Рис.5.
При синтезі n-розрядного компаратора порівняння операторів А і В користуються таблицею істинності з подальшою мінімізацією функцій порівнянняАіВ.
Арифметичний принцип порівняння двійкових n-розрядних чисел А і В можна здійснювати за допомогою суматора шляхом реалізації операції віднімання А-В і схеми аналізу отриманого результату.
Можливі 3 ситуації, які повинен зафіксувати компаратор
А>В; А=В і А<В
Відомо що операцію віднімання двох чисел можна замінити додаванням якщо код від’ємника перетворити наприклад у доповняльний код, який утворюється з оберненого шляхом додавання одиниці до молодшого розряду.
Аналогічно можна виконати функції порівняння за допомогою суматора.
Для цього:
1.код числа А подається на суматор у прямій формі;
2.код числа В подається на суматор у інверсній формі;
3.на вхід С1 переносу 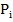 подається одиниця.
подається одиниця.
Тоді сигнали виходу суми Si і переносу Pi+1 визначатимуть результат порівняння. Зокрема якщо:
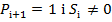 означає,щоА>В
означає,щоА>В
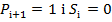 означає,щоА=В
означає,щоА=В
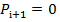 означає,щоА<B.
означає,щоА<B.
Цей алгоритм справедливий для додатних чисел А і В без врахування їх знаків.
Проілюструємо порівняння двох n-розрядних чисел А і В на прикладах що охоплюють три випадки.
1 випадок:А > В,нехай А=14; В=11
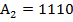 ;
;
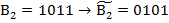 ;
; 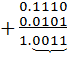
Ознакою А > В є 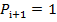 ;
; 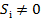 .
.
2 випадок А=В; А=В=11;
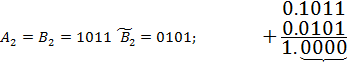
Ознакою A=Bє S=0; 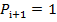
3 випадок А<В; А=11; В=14;
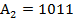 ;
;
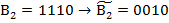 ;
; 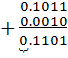
Ознакою A=B є 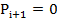 .
.
Схема чотирирозрядного компаратора, що реалізує арифметичний принцип порівняння.
| A0 S0
A1 SM S1
A2 S2
A3 S3
B1
B2
B3
B4
Ci C0
|
A=B
A
A>B(1)
B
Pi = 1 A<B(1)
Pi + 1
Промисловістю випускаються цифрові багаторозрядні компаратори як окремі вироби.
4-розрядрні ТТЛШ-555СП1; 531СП1.
| A0
A1 CMP
A2 A>B
A3
B0
B1 A=B
B2 A<B
B3
I >
I =
I <
|
Компаратори КМОН – 564ИП2; 561UИП2.
Вони мають додаткові інвертори для операнда В і додаткові три входи аналізуI>(A>B);I=(A=B) і I<(A<B). Останні призначені для утворення схеми нарощування розрядності операндів, тобто для каскадування послідовним або пірамідальним способом під’єднання однотипних мікросхем.


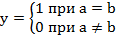 , (1)
, (1) .
.
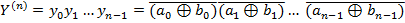
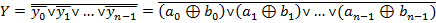
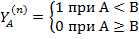 ;
; 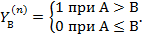
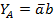 – заборона по a
– заборона по a – заборона поb.
– заборона поb.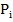 подається одиниця.
подається одиниця.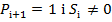 означає,щоА>В
означає,щоА>В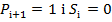 означає,щоА=В
означає,щоА=В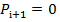 означає,щоА<B.
означає,щоА<B.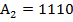 ;
;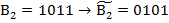 ;
; 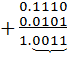
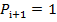 ;
; 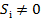 .
.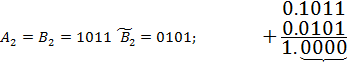
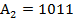 ;
;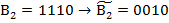 ;
; 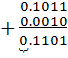
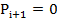 .
.