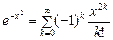1. Дано двовимірний масив А = {аij}, і = 1 ... n; j = 1, 2 ... m. Створити одновимірний масив В = {br} із його додатних компонентів.
Максимальне значення r = n×m, коли всі аij > 0. У пам’яті ЕОМ двовимірний масив (матриця) розміщується послідовно по рядках, отже, пошук елементів та їх обробка виконуються у такому самому порядку. Обробка двовимірного масиву організується як складний циклічний процес, зовнішній цикл — за рядками, внутрішній — за стовпчиками.
Побудуємо алгоритм обробки двовимірного масиву (рис. 5.33).

Рис. 5.33. Алгоритм обробки прямокутної матриці
2. Дано квадратну матрицю А = {аij}, і, j = 1, 2 ... n. Cформувати та надрукувати значення квадратів елементів її головної діагоналі.
Елементи головної діагоналі аіі. Одновимірний масив шуканих значень: В = {bi}, і = 1, 2 ... n. Побудуємо алгоритм визначення масиву В (рис. 5.34).

Рис. 5.34. Алгоритм обробки квадратної матриці
3. Дано матрицю А = {аij}, і = 1, 2 ... n; j = 1, 2 ... m. Вставити новий стовпчик, що складається з елементів вектора В = {bі}, і = 1 ... n; між r-им та (r + 1)-им стовпчиками (r < m).
Нова матриця С = {cik}, і = 1, 2 ... n; k = 1, 2 ... m + 1. Побудуємо алгоритм розширення матриці (рис. 5.35).

Рис. 5.35. Алгоритм вставки стовпчика у матрицю (початок)
4. Дано матрицю А = {аij}, і = 1, 2 ... n; j = 1 ... m. Знайти суму елементів, прилеглих по прямих напрямках до елемента аkr (1 < k < n, 1 < r < m), та записати її на місце елемента аkr.
5. Якщо рядок матриці А = {аij}, і = 1, 2 ... n; j = 1, 2 ... m; починається з від’ємного елемента, то треба змінити знак на протилежний у всіх елементів цього рядка. Вивести нову матрицю.
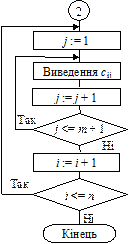
Рис. 5.35. Алгоритм вставки стовпчика у матрицю
Заняття 5: Ітераційні циклічні процеси
Запитання для перевірки знань
1. Які задачі розв’язують за допомогою наближених методів?
2. Як використовується розклад функції в ряд для обчислення її значень?
3. Розв’язання трансцендентних та алгебраїчних рівнянь високих степенів за допомогою методу хорд.
4. Визначення значень функцій за допомогою ітераційних методів.
Розглянемо використання методу хорд для розв’язання трансцендентних та алгебраїчних рівнянь високих степенів.
Сутність цього методу полягає в тому, що пошук кореня ведеться послідовним наближенням до його значення з використанням рівняння прямої, що проходить через дві точки, які належать графіку функції (тобто множині значень функції від аргументів із заданого відрізка). Наскільки близьким до кореня повинно бути шукане значення, покаже задана точність обчислень.
У загальному вигляді метод хорд можна представити таким чином.
Нехай маємо рівняння f(x) = 0. Треба знайти його корінь на деякому відрізку [а, b] з певною точністю e.
Перш за все необхідно визначити, чи належить відрізок [а, b] області визначення функції у = f(х). По-друге, щоб функція перетворилася на нуль на відрізку [а, b], необхідно, щоб її значення f(a) та f(b) мали протилежні знаки. Отже, її графік може набрати, наприклад, такого вигляду (рис. 5.36).

Рис. 5.36. Графік функції y = f(x)
Замінимо криву у = f(x) хордою, що проходить через точки
А(а, f(a)) та В (b, f(b)), яка перетне вісь ох у деякій точці х1. Рівняння прямої, що проходить через точки А та B:
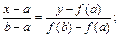
у = 0 в точці х = х1;
 .
.
Знайдемо точку А1(х1, f(х1)). Через неї та точку В(b, f(b)) проведемо нову хорду, яка перетне вісь ох у точці х2:
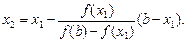
Продовжуючи цей процес, отримаємо
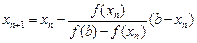 .
.
Отже, ми поступово наближаємось до шуканої точки, де функція перетворюється на 0, саме вона і буде значенням кореня рівняння. Важливо, що відстань між двома сусідніми значеннями точок х1 ... хn, хn+1 ... дедалі зменшується, разом із тим значення функції f(хn+1) зменшується і наближається до нуля, що дозволить припинити процес розв’язання рівняння f(х) = 0.
Оскільки для визначення хn+1 потрібне тільки хn, то для зручності перетворимо формулу:
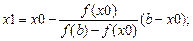
Побудуємо алгоритм (рис. 5.37)

Рис. 5.37. Загальний алгоритм розв’язання рівнянь методом хорд
Для розв’язання таких рівнянь можна використовувати метод дотичних, метод половинного ділення та інші.
Задачі
Використовуючи метод хорд, знайти корені рівнянь на заданих проміжках.
1. 2х + 5х – 3 = 0 –2<= x <= 2;
2. 3х4 + 4х3 — 12х2 — 5 = 0 0<= x <= 2;
3. Sin(х + p/ 3) – 0,5х = 0 –1 <= x <= 2;
4. 2ех = 7х –1<= x <= 1.
Використовуючи ітераційні формули, обчислити значення функцій
5. 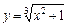 ;
;
6. 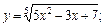
7. 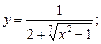
8. 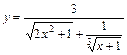
Використовуючи розклади функцій у ряди, обчислити їх значення:
9. 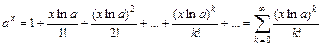 ;
;
10. 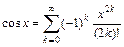 ;
;
11. 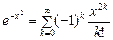






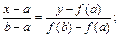
 .
.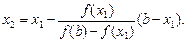
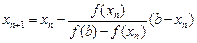 .
.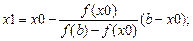

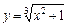 ;
;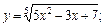
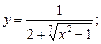
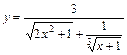
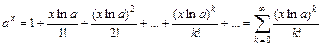 ;
;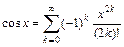 ;
;