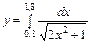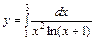1. Побудувати алгоритм обчислення значень функції
у = х tg (x/ 2) + 2 ln êcos (x/ 2) ê,
де х = 0,5; 0,6 ... 1,5.
Результат надрукувати у вигляді таблиці.
Для побудови цього алгоритму треба ввести граничні значення х1= 0,5, х2 = 1,5 та крок зміни h = 0,1. До тіла циклу входитимуть операції обчислення y та друку пap значень х, у.
2. Побудувати алгоритм обчислення найбільшого цілого додатного числа n, що задовольняє умову:
–n3+ 30n – 1 > 0.
Цей циклічний алгоритм відрізняється тим, що вихід із нього організується за допомогою перевірки умови, яку задано нерівністю. Отже, алгоритм матиме такий вигляд (рис. 5.26):
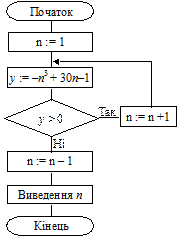
Рис. 5.26. Алгоритм задачі 2
3. Побудувати алгоритм знаходження у = х! (y =1× 2× 3 ... х)
4. Дано натуральне число n < 10000. S — сума його цифр. Побудувати алгоритм пошуку S.
Отже, маємо ціле число (не більше 4 цифр). Для обробки інформації, представленої у вигляді рядка цифр, використовують операції цілочисельного ділення div та mod, результатом операції div є найближче ціле число, що не перевищує частки від ділення.
7 div 3 = 2;
2 div 3 = 0.
Результатом операції mod є ціле число — остача від ділення:
7 mod 3 = 1;
2 mod 3 = 2.
Отже, використовуючи ці дві операції, можна визначити кількість цифр у числі, значення кожної цифри.
Алгоритм цієї задачі зображено на рис. 5.27.

Рис. 5.27. Алгоритм задачі 4
5. Дано натуральне число n. Утворити нове натуральне число m, взявши цифри числа n у зворотному порядку (n < 10000).
6. Дана послідовність 6 цифр. Чи може вона визначати дату? (ЧЧММГГ).
Існують класи задач, які є алгоритмічно нерозв’язними, але, використовуючи наближені методи, можна побудувати алгоритми їх розв’язання деяких підкласів або з деякими припущеннями, які не є суттєвими у певних умовах. До таких класів належать, наприклад, задачі інтегрування. Існують різні методи обчислення інтегралів. Розглянемо один із них, а саме — визначення інтегралу як площі, обмеженої графіком, підінтегральної функції (рис. 5.28).
| Рис. 5.29. Алгоритм обчислення визначеного інтегралу
|
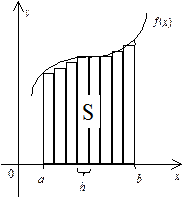 Рис. 5.28. Визначення інтегралу як площі фігури ò f(x)dx = S.
Рис. 5.28. Визначення інтегралу як площі фігури ò f(x)dx = S.
|
S можна обчислити як суму площ маленьких прямокутників, висота яких — значення f(x) у точках відрізку [а, b], отриманих із кроком h, а основа у всіх однакова — h. Таким чином, чим дрібніший крок розділення відрізку [а, b], тим ближче будуть значення S до результату інтегрування.
Побудуємо загальний алгоритм (рис. 5.29).
7. Побудувати алгоритм визначення інтегралу з кроком 0,01
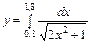
8. Побудувати алгоритм визначення інтегралу з кроком 0,01
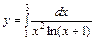
Заняття 3: Алгоритмізація обробки одновимірних масивів
Запитання для перевірки знань
1. Індекси масивів та циклічні змінні.
2. Принцип розміщення елементів масиву у пам’яті ЕОМ.
3. Організація обробки одновимірних масивів.


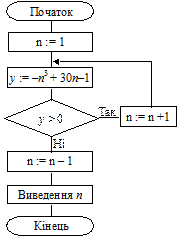

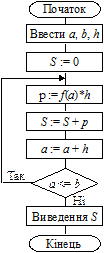
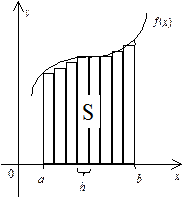 Рис. 5.28. Визначення інтегралу як площі фігури ò f(x)dx = S.
Рис. 5.28. Визначення інтегралу як площі фігури ò f(x)dx = S.