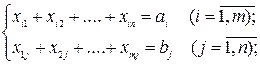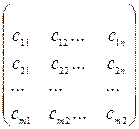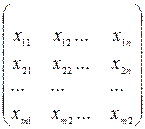Відноситься до задач лінійного програмування. В загальному вигляді транспортна задача може бути сформульована в наступному вигляді:
В заданих m пунктах виробництва (фабриках, заводах) А1, А2, ..., Аm виготовляється деякий однорідний продукт в кількостях а1, а2, ..., аm . Цю продукцію необхідно доставити в n заданих пунктів призначення (склади, магазини) В1, В2, ..., Вn в кількостях b1, b2, …, bn. Вартість перевозки одиниці вантажу з пункту аі в пункт bj відома і дорівнює сij, а відповідна кількість вантажу, який перевозиться з пункту аі в пункт bj позначають xij.
Сукупність m´n чисел xij , тобто матрицю 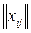 називають планом перевозок, а матрицю
називають планом перевозок, а матрицю 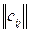 матрицею транспортних витрат.
матрицею транспортних витрат.
План називається допустимим, якщо числа xij задовольняють наступним умовам:
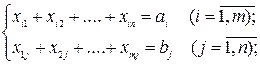
xij ³ 0 (i =1, m; j = 1, n )
в яких перші m рівнянь означають, що з кожного пунктах виробництва вивозиться весь виготовлений продукт, а останні n рівнянь означають, що потреби всіх споживачів повністю задовольняються.
Транспортна задача полягає в знаходженні серед допустимих планів xij такого, який мінімізував би загальну вартість перевозок, тобто треба знайти оптимальний план перевозок, при якому весь продукт з пунктів виробництва буде вивезено, а запити споживачів повністю задоволені і сумарні транспортні витрати були б мінімальні.
В загальному вигляді умова транспортної задачі виглядає таким чином:
Задана матриця перевозок:
Сij = 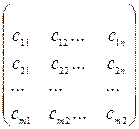
Знайти матрицю транспортних витрат:
Xij = 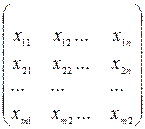


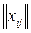 називають планом перевозок, а матрицю
називають планом перевозок, а матрицю 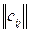 матрицею транспортних витрат.
матрицею транспортних витрат.