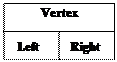First
Nil
Found
Рис 13.12. Вставка та вилучення елементу зі списку.
а) Пошук. Процедура Search здійснює пошук елемента списку з числом x у якості значення поля Data і повертає посилання Found на цей елемент. Якщо такий елемент у списку відсутній, Found = Nil.
Procedure Search(var Found, First: Point; x: Integer);
Begin
Found := First;
While (Found <> Nil) and (Found^.Data <> x)
do Found := Found^.Next
End;
б) Вставка. Процедура InsList добавляє елемент у список на місце, що передує Found^ (рис. 13.13). Посилання Found встановлюється на доданий елемент.
Procedure InsList(var Found: Point, x:Integer);
Var
p: Point;
Begin
New(p);
p^.Data := Found^.data;
Found^.Data := x;
p^.Next := Found^.Next;
Found^.Next := p
End;
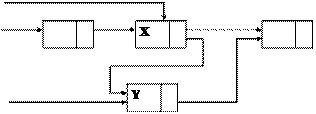 Found
Found
First
Р
Рис 13.13. Вставка елементу у список.
в) Вилучення. Процедура DelList вилучає з списку елемент Found^. Посилання Found встановлюється на елемент, що йде за вилученим.
Procedure DelList(Found: Point);
Var
p: Point;
y: Integer;
Begin
y := Found^.Next^.Data;
p:= Found^.Next;
Found^.Next := Found^.Next^.Next;
Found^.Data := y;
Dispose(p) {збирання сміття}
End;
 Found
Found
First
P
Рис 13.14. Вилучення елементу зі списку.
Відмітимо один явний недолік процедур InsList і DelList: вони непридатні для обробки останнього елемента списку! InsList для правильної роботи потребує наявності елемента Found^.Next^, а DelList – елемента Found^.Next^.Next. Тому, якщо треба вставити в список останній елемент, покажчик Found повинен бути виставлений на Nil, але тоді Found^.Next не визначений! Аналогічна ситуація має місце і при вилученні останнього елемента.
У нашій постановці задачі цей недолік виправити непросто. Суть ускладнень у тому, що до елементів списку, покажчики яких треба перекинути, немає прямого доступу: посилання Found виявляється встановленим на елемент, наступний за потрібним. Укажемо два виходи з цієї ситуації:
а) Останній елемент списку можна вважати ознакою кінця, поле Data якого не містить значущої інформації і покажчик Found на нього за умовою не може бути встановлений.
б) Можна змінити умови вставки-вилучення: посилання Found за умовою встановлюється на елемент, що передує місцю вставки або елементу, що вилучається. Тоді окремо (поза процедур) треба розглядати випадок, коли оброблюється 1-ий елемент. Самі ж процедури в цьому варіанті спрощуються.
Procedure Ins(var Found: Point, x:Integer);
Var
p: Point;
Begin
New(p);
p^.Data := x;
p^.Next := Found^.Next;
Found^.Next := p;
End;
Procedure Del(Found: Point);
Var
p: Point;
Begin
p:= Found^.Next;
Found^.Next = Found^.Next^.Next;
Dispose(p) {збирання сміття}
End;
Часто вставці/вилученню передує пошук місця зміни списку. Для правильної роботи процедур Ins і Del процедуру Search необхідно модифікувати. Переглядати список треба "на крок уперед". Розглянемо варіант процедури пошуку місця елемента з значенням поля Data = x у списку First із упорядкованими за зростаючими значеннями полів Data.
Procedure ForwardSearch(var Found, First: Point;
var isFirst: Boolean; x: Integer);
Begin
Found := First;
If First^.Data >= x
then isFirst := True
else begin
isFirst := False:
While (Found^.Next <> Nil) and (Found^.Next^.Data < x)
do Found := Found^.Next;
end
End;
Якщо isFirst = True, то місце – перше, інакше на місце вказує Found^.Next.
13.5. Задачі
Елемент списку описується наступним чином:
Type
Point = ^ Item;
Item = Record
Key: Integer;
Data: Real;
Next: Point
End;
Реалізувати процедуру злиття двох списків, елементи яких розташовані за зростанням значень полів Key. При рівних значеннях полів Key значення полів Data додаються. Оцінити складність алгоритму за часом у термінах довжин списків.
Реалізувати процедуру зчеплення (конкатенації) двох списків. Оцінити складність алгоритму за часом у термінах довжин списків.
Реалізувати процедуру сортування списку злиттям. Оцінити складність алгоритму за часом і пам’яттю (у гіршому випадку).
Реалізувати процедуру побудови списку, значущі елементи якого зберігаються у файлі F
а) F: File of Record Key: Integer; Data: Real End; із збереженням порядку розташування елементів у файлі. Оцінити складність алгоритму за часом.
б) F: File of Record Key: Integer; Data: Real End; Список повинен бути впорядкований за значеннями полів Key. Оцінити складність алгоритму за часом.
5.Реалізувати процедури Push і Pop відповідно добавлення і вилучення елемента для стека.
6.Реалізувати процедури Push і Pop відповідно добавлення і вилучення елемента для черги.
13.6. Дерева
Динамічні структури даних зручно визначати за допомогою рекурсивних визначень. Список, наприклад, визначається наступним чином:
 <список > ::= Nil | <елемент списку > < список >
<список > ::= Nil | <елемент списку > < список >
 Тут символ "::=" означає "є за визначенням", "|" - "або", " " - покажчик (посилання).
Тут символ "::=" означає "є за визначенням", "|" - "або", " " - покажчик (посилання).
Аналогічно можна визначити і структури, що розгалужуються – так звані дерева. Елемент такої структури (вузол дерева) визначається як запис, що містить декілька полів посилань. Наприклад:
Type
Point = ^ Item;
Item = Record
Data: Integer;
Right, Left: Point
End;
 Type
Type
Link = ^ TreeVert;
TreeVert = Record
Data: Real;
Key : Integer;
Left, Middle, Right : Link
End;
Рис 13.15. Структура вершини тернарного дерева
Кількість посилальних полів вузла дерева називається степенем розгалуження (арністю) вузла. Рекурсивне визначення дерева тоді має вид:
<дерево> ::= Nil | < вузол дерева >
<дерево> <дерево> . . . <дерево>
Таким чином, дерево може бути або виродженим (Nil), або складено з вузла дерева, всі покажчики якого виставлені на дерева. У цьому випадку вузол називають коренем дерева, а дерева, на які виставлені покажчики – піддеревами. Якщо піддерево складається з одного вузла, всі покажчики якого встановлені на Nil, його називають листом. Інші вузли дерева називають проміжними. Сукупність посилальних полів може бути оформлена як запис або як декілька полів запису (як у наших прикладах). Часто сукупність посилальних полів визначається в виді масиву посилань, або організується у виді списку посилань. У цих випадках говорять про впорядковані дерева, так як піддерева одного кореня виявляються впорядкованими або індексами масиву, або за порядком доступу. Якщо всі вузли дерева мають один і той же степінь розгалуження, можна говорити про степінь розгалуження дерева. Дерева, степінь розгалуження яких дорівнює двом, називають бінарними. Бінарні дерева – одна з найбільш поширених структур, що розгалужуються, які застосовуються у програмуванні.
13.7. Бінарні дерева
Бінарне дерево має вид
T(v)
v


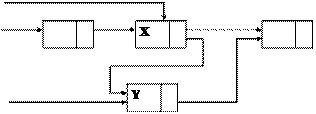 Found
Found Found
Found <список > ::= Nil | <елемент списку > < список >
<список > ::= Nil | <елемент списку > < список > Тут символ "::=" означає "є за визначенням", "|" - "або", " " - покажчик (посилання).
Тут символ "::=" означає "є за визначенням", "|" - "або", " " - покажчик (посилання). Type
Type