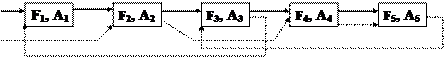Наприклад:
[ ] - порожня множина
[2, 5 ..7] - множина {2, 5, 6, 7}
['A'..'Z', 'O'..'9'] - множина, що складається з всіх великих латинських букв і цифр
[i + j .. i + 2*j] - множина, що складається з всіх цілих чисел між i + j і i + 2j
Відмітимо, що якщо у виразі [v1..v2] v1 > v2, множина [v1 .. v2] - порожня.
12.3. Операції і відношення над множинами
До операндів - однотипних множин А і В можна застосувати такі дії:
А + В - об’єднання А È В
А * В - перетин А Ç В
А - В - різниця А \ В
Між А і В визначені також відношення порядку і рівності
А = В, А <> В, А < В, А <= В, А > В, А >= В;
Відношення порядку інтерпретуються як теоретико-множинні включення.
Якщо А – множина і х – елемент базового типу, то визначено відношення належності х in A - x належить A ( x Î A ).
Кожне з відношень, описаних вище, по суті є операцією, результат якої має тип Boolean. Таким чином, якщо Init – змінна типу Boolean, можливе присвоювання Init := A < B. Можливі такі порівняння ( А = В ) = ( С = D ).
Наявність операцій над множинами дозволяє застосовувати в програмах оператори присвоювання, в лівій частині яких стоїть змінна типу множини, а в правій – вираз того ж типу. Наприклад:
А := А * [1 .. 10] + B ; B := (А + B)*['A' .. 'Z'] ;
12.4. Застосування множин у програмуванні
При реалізації мови розміри множин завжди обмежені константою, що залежить від реалізації. Звичайно ця константа кратна довжині машинного слова. Це відбувається тому, що множини реалізовані в виді логічних (двоїстих) векторів наступним чином: кожній координаті двоїстого вектора однозначно відповідає один з елементів базового типу. Якщо елемент а належить множині А, що представляється, то значення координати вектора, відповідне а, дорівнює 1. У протилежному випадку значення відповідної координати дорівнює 0.
Наприклад, якщо множина А описана як Set of 0..15, то його представляє 16-ти мірний двоїстий вектор, координати якого перенумеровані від 0 до 15, і і-тій координаті відповідає елемент і базового типу.
Базовий тип : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Двоїстий вектор : 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 0
Представлена множина : A = [2, 3, 5, 7, 11, 13]
Такий спосіб реалізації дозволяє швидко виконувати операції над множинами і перевірки теоретико-множинних відношень. Тому, наприклад, замість
For X := 'A' to 'Z' do
If (X ='A') or (X ='E') or (X ='I') or (X ='O') or (X='U')
then Statement1
else Statement2
краще написати
For X := 'A' to 'Z' do
If X in ['A','E','I','O','U']
then Statement1
else Statement2
Остання форма запису не тільки краще читається, але й значно швидше обчислюється.
У Pascal максимальна кількість елементів у множині дорівнює 256. Таким чином, у якості базового типу можна вибирати, наприклад, Char або відрізок 0..255. У завершення розділу наведемо приклад програми, що використовує множинні типи даних.
Приклад 12.1. Побудувати множину всіх простих чисел з відрізка 2..n (n £ 255).
Метод, за допомогою якого ми це зробимо, відомий як “Решето Ератосфена”. Суть цього метода у наступному: Нехай Prime - множина простих чисел, що будується, і Grating - множина, що називається решетом. Алгоритм починає роботу з Prime = [ ]; Grating = [2..n].
Крок основного циклу:
а. Найменший елемент Grating помістити у Prime;
б. Вилучити з Grating всі числа, кратні цьому елементу;
Алгоритм закінчує роботу при Grating = [ ]
Program EratosfenGrating;
Const
n = 255;
Type TSet= set of 2 .. n ;
Var Prime: TSet;
Procedure PrimeNumber(Var Prime: TSet);
Var
Grating: TSet;
i, Min : integer ;
Begin
Grating := [2 .. n] ;
Prime := [] ;
Min := 2; {ініціалізація}
While Grating <> [] do begin {основний цикл}
While not(Min in Grating) do
{пошук найменшого елемента в решеті}
Min := Min + 1;
Prime := Prime + [Min] ;
{поповнення множин простих чисел}
For i := 1 to n div Min do {вилучення кратних із решета}
Grating := Grating - [i*Min];
end;
End;
Procedure OutSet (Prime: TSet);
Var i:Integer;
Begin
Writeln('Primes: '); {виведення множин простих чисел}
For i := 1 to n do
If i in Prime then write(i, ', ');
End;
Begin
PrimeNumber(Prime);
OutSet (Prime);
End.
Відмітимо, що доступ до елемента множини у мові не передбачений. У цьому – ще одна якісна відміна множинного типу від інших типів даних. Тому наприклад, для введення множини Prime доводиться перебирати всі елементи базового типу і кожний із них перевіряти на належність Prime.
12.5. Задачі і вправи
Записати за допомогою конструктора множину Х, яка складена з латинських букв a, b, c, d, i, j, k, x, y, z.
Записати за допомогою конструктора множину з трьох основних кольорів множинного типу Paint.
Записати за допомогою конструктора множину цілих розв’язків квадратної нерівності x^2 +p*x + q < 0 у припущенні, що корні відповідного квадратного рівняння лежать в інтервалі [0; 255].
Записати за допомогою конструктора множину простих чисел-близнюків з інтервалу 1..30.
13. Динамічні структури даних
У попередніх параграфах були визначені фундаментальні структури даних, що використовуються у процедурному програмуванні: масиви, записи, файли і множини. Фундаментальність цих структур означає, що вони, по-перше, частіше всього використовуються в практиці програмування, і, по-друге, визначають методи структурування даних – тобто методи утворення складних структур із більш простих. Наприклад, можна визначити масив із записів, запис, що складається з множин, файл із масивів, компоненти яких – записи, і т.д. Для кожної з таких структур даних характерна та обставина, що розмір пам’яті, що відводиться для неї, визначається компілятором під час компіляції розділів типів і змінних і залишається незмінним під час виконання програми. Тому такі змінні-структури називаються статичними. Наряду з статичним розподілом пам’яті ми вже використовували в програмах і динамічний розподіл пам’яті – під локальні змінні процедур і функцій. Особливо випукло динамізм тут проявляється при використанні рекурсії.
Однак багато задач для своєї ефективної реалізації потребують явних методів динамічного використання пам’яті, тобто описання таких структур даних, розмір і конфігурація яких змінюються під час виконання програм. Такі структури даних називаються динамічними.
Приклад 13.1. Уявимо собі, що наша програма повинна деяким чином обробляти послідовність символів, яка представляє математичну формулу (арифметичний вираз). Якщо обробка пов’язана з обчисленням значення цієї формули, то представлення формули в виді рядка символів неприродно. Зручніше представити, наприклад, формулу f = (a + b)*(a - c) у виді наступної структури:

Рис. 13.1. Представлення формули динамічною структурою.
Тепер обчислення значення f можна організувати “знизу-вгору”, підставляючи результати операції замість знаків операцій. Легко бачити, що такий метод обчислення є універсальним.
Приклад 13.2. Нам треба обробити набір відомостей про людей (прізвище - F, вік - А), причому обробка включає процедури включення людини у список, вилучення зі списку, виведення списку як у алфавітному порядку по прізвищам, так у порядку зменшення віку. Дані для цієї задачі зручно уявити у виді структури:
Рис. 13.2. Представлення набору даних динамічною структурою.
в якій Fi – прізвища, Ai – вік людей, суцільні стрілки вказують на людей що йдуть в алфавітному порядку., а пунктирні – на людей, що йдуть за ростом.
Тоді включення – вилучення елементів можна робити переорієнтацією стрілок, а порядок виведення легко отримати, слідуючи по відповідним стрілкам. Нижче ми розглянемо і інші приклади задач, у програмуванні яких зручно використовувати динамічні структури.
Розглянуті приклади показують, що динамічні структури даних представляють із себе сукупність елементів, кожний з яких містить як деяку значущу інформацію, так і інформацію про зв’язки з іншими елементами структури. Інформацію про зв’язки називають посиланнями або покажчиками.
Динамічні структури даних, що реалізуються засобами мови Паскаль, представляються у виді сукупності записів, кожна з яких містить інформаційні поля і поля посилань (покажчиків) на інші записи структури.
Інформаційні поля Поля покажчиків
Рис. 13.3. Запис - елемент динамічної структури.
Посилання на деякий елемент – це по суті адреса першого (молодшого байта) фрагмента оперативної пам’яті, відведеної під цей елемент.
Для реалізації ефективних алгоритмів розв’язків задач вирішальну роль грають способи об’єднання елементів у структури даних. Для кожного такого способу характерна як топологія структури, так і методи її обробки. Нижче ми розглянемо деякі з таких динамічних структур, які по суті є стандартними (типовими).
13.1. Стандартні динамічні структури
У програмуванні часто використовують наступні динамічні структури: списки, стеки, черги, дерева, графи і т.д. Точні математичні визначення цих структур, як ми побачимо нижче, використовують рекурсивні описання. Для попередніх пояснень краще всього використовувати графічні зображення.