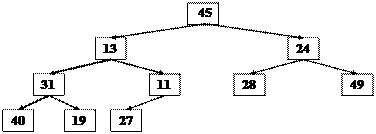Відмітивши, що при N = 1 задача розв’язується за допомогою процедури Step (I, J), опишемо процедуру HanojTower (N,I,J):
Procedure HanojTower(N, I, J: Integer);
Begin
If N = 1
then Step(I, J)
else begin
HanojTower(N-1, I, 6-I-J);
Step(I, J);
HanojTower(N-1, 6-I-J, J)
end
End;
Процедуру Step(I, J) можна реалізувати, використовуючи представлення даних у масиві Rings[1..N, 1..3] і графічну візуалізацію переміщення кілець.
Визначимо складність алгоритму за часом C(n) (кількість кроків-викликів Step), вписавши рекурентне співвідношення: С(n) = 2C(n-1) + 1
Легко тепер довести, що С(n) = 2n - 1. Доведено, що ця кількість кроків є мінімально можливою, тому наш алгоритм оптимальний.
Приклад 9.5. Лінійні діафантові рівняння
Перелічити всі невід’ємні цілі розв’язки лінійного рівняння a1x1 + a2x2 + ... + anxn = b з цілими додатними коефіцієнтами.
Як і в попередніх прикладах, опишемо алгоритм рекурсивно, здійснивши зведення вихідної задачі до задачі меншого розміру.
Перепишемо вихідне рівняння у виді:
a1 x1 + a2 x 2 + ... + a n-1 x n-1 = b - a n x n
Організуємо перелік всіляких значень xn, при яких права частина b - a n x n > 0. xn = 0, 1, ... y, де y = b div an. Тоді перші n-1 компонент розв’язка (x1, ... , x n-1, x n) вихідного рівняння – розв’язок рівняння
a1 x1 + a2 x2 + ... + a n-1 x n-1 = b - a n x n .
Таким чином ми звели розв’язок вихідного рівняння до розв’язку у+1 рівняння з n-1 невідомим, і, отже, можемо реалізувати алгоритм рекурсивно. Визначимо умови виходу з рекурсії:
при b = 0 існує єдиний розв’язок – (0, 0, ..., 0)
при n = 1 якщо b mod a1 = 0 то x1 = b div a1 інакше розв’язків немає.
Таким чином, виходити з рекурсивних обчислень треба в двох (крайніх) випадках. Ми встановили і параметри процедури: n і b.
Procedure Solution(n, b : integer);
Var
i, j, y, z : Integer;
Begin
If b = 0
then begin
For j := 1 to n do X[j] := 0;
WriteSolution
end
else If (n = 1) and (b mod a[1] = 0)
then begin
X[1]:= b div a[1];
WriteSolution
end
else If n > 1
then begin
z := a[n];
y := b div z;
For i := 0 to y do begin
X[n] := i;
Solution(n - 1, b - z*i)
end
end
End;
Program AllSolutions;
Const
n = 4;
Type
Vector = array[1..n] of Integer;
Var
a, X : Vector;
b : Integer;
i : Integer;
{Procedure WriteSolution друкує розв’язок X[1..n] }
{Procedure Solution}
Begin
{Введення масиву коефіцієнтів a[1..n] і св. члена b}
Solution(n, b)
End;
Приклад 9.6. Піднесення числа до натурального степеня
Піднести дійсне число а у натуральний степінь n.
Раніше ця задача була розв’язана методом послідовного домноження результату на а. Однак її можна розв’язати ефективніше, якщо застосувати метод половинного ділення степеня n. Саме: an = (a n/2) )2. Оскільки число n не обов’язково парне, формулу треба уточнити:
a^n = (a n div 2) 2 * a n mod 2. Доповнивши визначення a n визначенням a1 = a і замінивши домноження на a n mod 2 розбором випадків парний-непарний, отримаємо:
Function CardPower(a : Real; n : Integer) : Real;
var
b : Real;
Begin
If n = 1
then CardPower := a
else begin
b := Sqr(CardPower(a, n div 2));
If n mod 2 = 0
then CardPower := b
else CardPower := a*b
end
End;
Доведіть, що функція CardPower використовує не більш O(log2n) множень і піднесень у квадрат.
Приклад 9.7. Перетин зростаючих послідовностей
Нехай A = [a1, a2,...,an] і B = [b1, b2, ... , bm] – дві зростаючі числові послідовності. Перетином цих послідовностей називається зростаюча послідовність С = [с1, с2,..., сk], що складається з тих і тільки тих чисел, які належать обом послідовностям. Треба знайти C = AÇB.
Зведемо задачу до кількох підзадач, більш простих, ніж вихідна. Поділимо для цього вихідні послідовності на частини
A = [a1]ÈA2; B = [b1] È B2, де A 2 = [a 2,...,a n], B 2 = [b 2,...,b n]
Тоді
AÇB = (a1 È A2) Ç(b1 + B2) = a1Çb1 È a1ÇB2 È A2Çb1 È A2ÇB2
(Дужки в позначеннях одноелементних множин опущені)
Так як послідовності A і B зростають, маємо:
Якщо a1 = b1 то AÇB = a1Çb1 È A2ÇB2 = a1 È A2ÇB2
Якщо a1 < b1 то AÇB = b1ÇA2 È A2ÇB2 = A2ÇB
Якщо a1 > b1 то AÇB = a1ÇB2 È A2ÇB2 = AÇB2
Ці відношення зводять вихідну задачу до задач менших розмірів, тому їх можна використовувати для рекурсивного описання обчислень.
Процедура Intersect пошуку перетину залежить від параметрів i та j – номерів початкових елементів підпослідовностей A[i..m] і B[j..n], представлених масивами A[1..m] і B[1..n]. Знайдений елемент перетину роздруковується.
Procedure Intersect(i, j : Integer);
Begin
If (i <= m) and (j <= n)
then If a[i] = b[j]
then begin
Write(a[i]);
Intersect(i+1, j+1)
end
else If a[i] < b[j]
then Intersect(i+1, j)
else Intersect(i, j+1)
End;
9.3. Переваги і недоліки рекурсивних алгоритмів
Розглянуті приклади показують, що застосування рекурсивних означень само по собі не приводить до хороших розв’язків задач. Так, задачі прикладів 9.1, 9.3, 9.6 допускають більш ефективні і достатньо прості ітеративні розв’язки. У прикладі 9.1 це продемонстровано особливо наочно. У прикладах рекурсія моделює простий цикл, який витрачає час на обчислення, що пов’язані з керуванням рекурсивними викликами і пам’ять на динамічне збереження даних. Ми вже розглядали ітеративну версію метода ділення навпіл в інших прикладах.
Безсумнівним достоїнством алгоритмів з прикладів 9.1, 9.3, 9.6 є їх простота і обгрунтованість. При програмуванні ми по-суті одночасно обгрунтовували правильність алгоритму. У прикладах 9.2, 9.5, 9.7 розглядались комбінаторні задачі, розв’язки яких не зводяться до простого застосування циклу, а потребують перебору варіантів, природнім чином, що керується рекурсивно. Ітеративні версії розв’язків цих задач складніші по управлінню. Можна сказати, що основна обчислювальна складність комбінаторної задачі полягає не в реалізації алгоритму її розв’язку, а в самому методі розв’язку.
Пізніше ми побачимо, як рекурсія в поєднанні з іншими методами використовується для побудови ефективних програм.
9.4. Задачі і вправи
Вправа І.
Опишіть процедуру пошуку найбільшого і найменшого елементів у масиві. За допомогою цієї процедури складіть програму, що визначає, чи співпадають найбільший і найменший елементи двох масивів А [1..n] і В [1..n].
Опишіть процедури пошуку середнього за величиною елемента у масиві А [1..2n+1] і середнє арифметичне елементів цього масиву. За допомогою цих процедур складіть програму, яка порівнює середнє за величиною і середнє арифметичне у масиві А [1..99].
Опишіть процедуру пошуку найбільшого і найменшого елементів у масиві А[1..n]. За допомогою цієї процедури складіть програму, що визначає координати вершин найменшого прямокутника зі сторонами, паралельними осям координат, який містить в собі множину точок Т1(X1,Y1), ... , Tn(Xn,Yn).
Опишіть процедуру перевірки розкладення натурального числа в суму двох квадратів. Складіть програму, яка вибирає з даного масиву ті і тільки ті числа, які розкладаються в суму двох квадратів.
Опишіть функцію перевірки простоти числа. Опишіть функцію перевірки числа на розкладність в суму виду 1+2а. Складіть програму, яка вибирає з даного масиву чисел ті і тільки ті його елементи, які задовольняють обом властивостям.
Опишіть процедуру перетворення цілого числа з десяткової системи в p-ічну систему числення. Опишіть процедуру перетворення правильного десяткового дробу в p-ічний з заданою кількістю розрядів. Складіть програму перетворення довільного дійсного числа з 10-вої в p-ічну систему числення.
Опишіть процедуру пошуку найменшого елемента в рядку матриці. Опишіть функцію перевірки на максимальність даного елемента в стовпці матриці. Складіть програму пошуку сідлової точки матриці.
Вправи II.
1.Опишіть функцію f(x) - найбільший власний дільник числа х. Складіть програму пошуку всіх власних дільників числа N.
2.Опишіть функцію y = arcsin(x). Складіть програму розв’язку рівняння sin(ax+b) = c.
3.Опишіть функцію f(x) = max (t*sin(t)).
t Î [0,x]
Складіть Програму табулювання функції f(x) на відрізку [a,b].
4.Опишіть функцію f(x) - число, яке отримується з натурального числа x перестановкою цифр у зворотному порядку. Складіть програму, яка роздруковує симетричні числа з масиву натуральних чисел.
Задачі.
1.Перечислити всі вибірки по K елементів у масиві A з N елементів. Масив містить перші N натуральних чисел: A[i] = i. Знайти їх кількість і оцінити складність алгоритму.
2.Перечислити всі підмножини множини (масиву A) з задачі 1. Знайти їх кількість і оцінити складність алгоритму.
3.Дано масив A[1..n] цілих додатних чисел і ціле число b. Перечислити всі набори індексів j1, j2, ..., jk такі, що A[j1] + A[j2] + ... + A[jk] = b. Оцінити складність алгоритму.
4.Дано масив A[1..n] цілих чисел і ціле число b. Перечислити всі набори індексів j1, j2, ... , jk такі, що A[j1] + A[j2] + ... + A[jk] = b. Оцінити складність алгоритму.
5.Відома в теорії алгоритмів функція Акермана А(x, y) визначена на множні натуральних чисел рекурсивно:
A(0, y) = y + 1,
A(x, 0) = A(x - 1, 1),
A(x, y) = A(x - 1, A(x, y - 1));
a)Опишіть функції A(1, y), A(2, y), A(3, y), A(4, y) явним чином;
б)Реалізуйте рекурсивну програму обчислення A(x, y);
в) Реалізуйте програму обчислення A(x, y) без рекурсії.
10. ШВИДКІ АЛГОРИТМИ СОРТУВАННЯ І ПОШУКУ
У цьому параграфі ми завершимо вивчення алгоритмів сортування і пошуку в масивах, розглянувши так звані швидкі методи сортування.
10.1. Нижня оцінка часу задачі сортування масиву за числом порівнянь
Можна довести, що будь-який алгоритм сортування масиву, що використовує тільки порівняння і перестановки, у гіршому випадку потребує мінімум O(n log2 n) порівнянь. Таким чином, функція складності в гіршому випадку алгоритму сортування С(n) обмежена знизу величиною O(n log2 n).
Пам’ятаймо, що алгоритм сортування вставками має таку ж саму за порядком величини функцію С(n).
Питання про оцінку оптимальної кількості перестановок М(n) ми розглянемо нижче. Можна припустити, що кожній перестановці передує деяке порівняння. Тоді загальна кількість перестановок, що здійснюється алгоритмом, не перевищує С(n) і, отже, ефективні алгоритми сортування повинні мати складність O(n*log2n) як за порівняннями, так і за перестановками. Зараз ми розглянемо деякі такі алгоритми.
10.2. Швидкі алгоритми сортування: Сортування деревом
Алгоритм сортування деревом ТreeSort по суті є поліпшенням алгоритму сортування вибором. Процедура вибору найменшого елементу вдосконалена як процедура побудови так званого дерева сортування. Дерево сортування – це структура даних, у якій представлений процес пошуку найменшого елемента методом попарного порівняння елементів, що стоять поряд. Алгоритм сортує масив у два етапи.
І етап: побудова дерева сортування;
ІІ етап: просівання елементів по дереву сортування.
Розглянемо приклад:
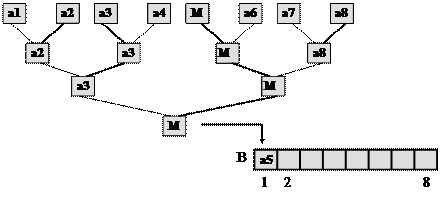
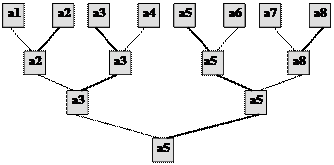
Нехай масив А складається з 8 елементів (мал. 10.1, 1-ий рядок). Другий рядок складається з мінімумів елементів першого рядка, що стоять поряд. Кожний наступний рядок складається з мінімумів елементів попереднього, що стоять поряд.
 a2 = min(a1,a2)
a2 = min(a1,a2)
a3 = min(a3,a4)
a5 = min(a5,a6)
a8 = min(a7,a8)
a3 = min(a2,a3)
a5 = min(a5,a8)
a5 = min(a3,a5)
Рис 10.1. Дерево сортування масиву з 8-ми елементів.
Цю структуру даних називають деревом сортування. У корені дерева знаходиться найменший елемент. Крім цього, в дереві побудовані шляхи елементів масиву від листя до відповідного за величиною елемента вузла – розгалуження. (На рис. 10.1 шлях мінімального елемента а5 – від листа а5 до кореня відмічений товстою лінією.)
Коли дерево побудовано, починається етап просівання елементів масиву по дереву. Мінімальний елемент пересилається у вихідний масив В і всі входження цього елемента в дереві замінюються на спеціальний символ М.
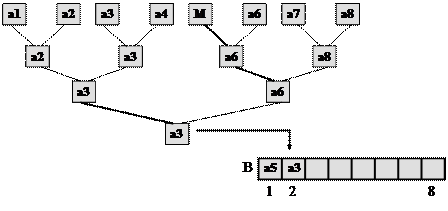
Рис. 10.2. Просівання найменшого елементу
Потім здійснюється просівання елемента уздовж шляху, відміченого символом М, починаючи з листка, сусіднього з М (На рис. 10.2 зверху-вниз) і до кореня. Крок просівання – це вибір найменшого з двох елементів, що зустрілись на шляху до кореня дерева і його пересилання у вузол, відмічений М. Просівання 2-го елемента показано на мал. 10.3 (Символ М більше, ніж будь-який елемент масиву.)
a6 = min(M, a6)
a6 = min(a6, a8)
a3 = min(a3, a6)
b2 := a3
Рис.10.3. Просівання 2-го елемента
Просівання елементів відбувається до тих пір, поки весь вихідний масив не буде заповнений символами М, тобто n разів:
For I := 1 to n do begin
Відмітити шлях від кореня до листка символом М;
Просіяти елемент уздовж відміченого шляху;
B[I] := корінь дерева
end;
Обгрунтування правильності алгоритму очевидне, оскільки кожне чергове просівання викидає у масив В найменший з елементів масиву А, що залишився.
Дерево сортування можна реалізувати, використовуючи або двомірний масив, або одномірний масив ST[1..N], де N = 2n-1 (див. наступний розділ).
10.2.1. *Аналіз складності алгоритму
Оцінимо складність алгоритму в термінах M(n), C(n). Перш за все відмітимо, що алгоритм TreeSort працює однаково на всіх входах, так що його складність у гіршому випадку співпадає зі складністю в середньому.
Припустимо, що n - степінь 2 (n = 2l). Тоді дерево сортування має l + 1 рівень (глибину l). Побудова рівня I потребує n / 2I рівнянь і пересилань. Таким чином, I-ий етап має складність
C1(n) = n/2 + n/4 + ... + 2 + 1 = n - 1, M1(n) = C1(n) = n - 1
Для того, щоб оцінити складність II-го етапу С2(n) і M2(n) відмітимо, що кожний шлях просівання має довжину l, тому кількість порівнянь пересилань при просіванні одного елемента пропорційна l. Таким чином, M2(n) = O(l n), C2(n) = O(l n).
Оскільки
l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n),
але С(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n).
Так як C1(n) < C2(n), M1(n) < M2(n),
остаточно отримаємо оцінки складності алгоритму TreeSort за часом:
M(n) = O(n log2 n), C(n) = O(n log2 n),
У загальному випадку, коли n не є степенем 2, дерево сортування будується дещо по іншому. “Зайвий” елемент (елемент, для якого немає пари) переноситься на наступний рівень. Легко бачити, що при цьому глибина дерева дорівнює [log2 n] + 1. Удосконалення алгоритму II етапу очевидне. Оцінки при цьому міняють лише коефіцієнти-множники. Алгоритм TreeSort має суттєвий недолік: для нього потрібна додаткова пам’ять розміром 2n - 1.
10.3. Пірамідальне сортування
Алгоритм пірамідального сортування HeapSort також використовує представлення масиву у виді дерева. Цей алгоритм не потребує додаткових масивів; він сортує “на місці”. Розглянемо спочатку метод представлення масиву у виді дерева:
Нехай А [1 .. n] – деякий масив. Зіставимо йому дерево, використовуючи наступні правила:
1. A[1] - корінь дерева ;
2. Якщо A[i] - вузол дерева і 2i £ n,
то A[2*i] - вузол - “лівий син” вузла A[i]
3. Якщо A[i] - вузол дерева і 2i + 1 £ n,
то A[2*i+1] - вузол - “правий син” вузла A[i]
лівий син правий син
батько
Рис 10.4. Правило представлення дерева в масиві.
Правила 1 - 3 визначають у масиві структуру дерева, причому глибина дерева не перевищує [log2 n] + 1. Вони ж задають спосіб руху по дереву від кореня до листя. Рух уверх задається правилом 4:
4.Якщо A[i] - вузол дерева і i > 1
то A[i mod 2] - вузол - “батько” вузла A[i];
Приклад 10.1. Нехай A = [45 13 24 31 11 28 49 40 19 27] – масив. Відповідне йому дерево має вид:
Рис. 10.5 Представлення масиву в дереві.
Зверніть увагу на те, що всі рівні дерева, за винятком останнього, повністю заповнені, останній рівень заповнений зліва і індексація елементів масиву здійснюється зверху-вниз і зліва-направо. Дерево впорядкованого масиву задовольняє наступним властивостям:
A[i] £ A[2*i], A[i] £ A[2*i+1], A[2*i] £ A[2*i+1].
Як це не дивно, алгоритм HeapSort спочатку будує дерево, яке задовольняє прямо протилежним співвідношенням
A[i] ³ A[2*i], A[i] ³ A[2*i+1] (6)
а потім міняє місцями A[1] (найбільший елемент) і A[n].
Як і TreeSort, алгоритм HeapSort працює в два етапи:
І.Побудова дерева, що сортує;
І І.Просівання елементів по дереву, що сортує.
Дерево, що представляє масив, називається сортуючим, якщо виконуються умови (6). Якщо для деякого і ця умова не виконується, будемо говорити, що має місце (сімейний) конфлікт у трикутнику і (Рис.10.4).
І на І-ому, і на ІІ-ому етапах елементарна дія алгоритму полягає у розв’язку сімейного конфлікту: якщо найбільший з синів більше, ніж батько, то переставляються батько і його син (процедура ConSwap).
У результаті перестановки може виникнути новий конфлікт в тому трикутнику, куди переставлений батько. Таким чином можна говорити про конфлікт (роду) у піддереві з коренем у вершині і. Конфлікт роду розв’язується послідовним розв’язком сімейних конфліктів – проходом по дереву зверху-вниз. (На Рис.10.5 шлях розв’язку конфлікту роду у вершині 2 відмічений.) Конфлікт роду розв’язаний, якщо прохід завершився (i > n div 2) або у результаті перестановки не виникнув новий сімейний конфлікт. (процедура Conflict)
Procedure ConSwap(i, j : Integer);
Var b : Real;
Begin
If a[i] < a[j]
then begin
b := a[i];
a[i] := a[j];
a[j] := b
end
End;
Procedure Conflict(i, k : Integer);
Var
j : Integer;
Begin
j := 2*i;
If j = k
then ConSwap(i, j)
else if j < k
then begin
if a[j+1] > a[j]
then j := j + 1;
ConSwap(i, j);
Conflict(j, k)
end
End;
I етап - побудови дерева, що сортує – оформимо в виді рекурсивної процедури, використовуючи визначення:
Якщо ліве і праве піддерева T(2i) і T(2i+1) дерева T(i) , що сортують, то для перебудови T(i) необхідно розрішити конфлікт роду в цьому дереві.
Procedure SortTree(i : Integer);
begin
If i <= n div 2
then begin
SortTree(2*i);
SortTree(2*i+1);
Conflict(i, n)
end
end;
На II-ому етапі - етапі просівання - для k от n до 2 повторюються наступні дії:
1.Переставити A[1] і A[k];
2.Побудувати дерево, що сортує початкового відрізка масиву A[1..k-1], усунувши конфлікт роду в корені A[1]. Відмітимо, що 2-а дія потребує введення в процедуру Conflict параметра k.
Program HeapSort;
Const
n = 100;
Var
A : Array[1..n] of real;
k : Integer;
{процедури ConSwap, Conflict, SortTree, введення, виведення}
Begin
{ введення }
SortTree(1);
For k := n downto 2 do begin
ConSwap(k, 1);
Conflict(1, k - 1)
end;
{ виведення }
End.
10.3.1.*Аналіз складності алгоритму
Оцінимо складність алгоритму у термінах C(n), M(n). Оскільки кожна перестановка пов’язана з порівняннями в процедурі ConSwap, M(n) £ C(n). Далі, в процедурі Conflict порівняння передує виклику ConSwap, тому загальне число порівнянь не перевищує подвоєного числа викликів ConSwap. Отже, С(n) можна отримати, оцінивши кількість звернень до ConSwap.
Складність I-го етапу C1(n) задовольняє співвідношенню
C1(n) £ 2C1(n / 2) + C0(n)
де C0(n) - складність процедури Conflict(1, n).
Для С0(n) маємо:
C0(n) £ C0(n/2) + 1,
оскільки виклик Conflict(i, n) містить один (рекурсивний) виклик Conflict(2i, n) і ланцюжок викликів обривається при i > n/2. Тому
C0(n) £ c0 log2 n.
Таким чином,
C1(n) £ 2 C1(n / 2) + c0 log2 n.
Нехай k - деяке число. Тоді
C1(n) <= 2 k C1(n/2k) +c0 (2 k-1 log2(n/2 k-1) + ...+ log2(n/2) log2 n)
Оскільки С1(1) = 0, маємо
C1(n) <= c0 (log2 n + 2 log2(n/2) + ... (n/2) log2(2)).
Замінимо log( n/2 i ) на log2 n, посиливши нерівність. Отримаємо
C1(n) <= (c0 log2 n)(1 + 2 + 4 + ... n/2)
Сума в дужках не перевищує n. Тому
C1(n) <= с0 n log2 n (7)
Арифметичний цикл II-го етапу виконується n - 2 разів і кожне повторення містить ConSwap(k, 1) і Conflict(1, k - 1). Тому його складність C2(n) можна оцінити нерівністю C2(n) <= (1+C0(n-1)) + (1+C0(n-2)) + ... + (1+C0(2)) Замінимо C0(i) на C0(n-1), посиливши нерівність. Отримаємо
C2(n) <= n + n C0(n-1) = c1 n log2 n (8)
Остаточно С(n) = C1(n) + C2(n) = (c0+c1) n log2 n, або
С(n) = O( n log2 n ) (9)
Ми показали, що пірамідальне сортування (з точністю до мультиплікативної константи) оптимальне: його складність співпадає ( з тією ж точністю) з нижньою оцінкою задачі.
10.4. Швидке сортування Хоара
Удосконаливши метод сортування, оснований на обмінах, К.Хоар запропонував алгоритм QuickSort сортування масивів, що дає на практиці відмінні результати і дуже просто програмується. Автор назвав свій алгоритм швидким сортуванням.
Ідея К.Хоара полягає у наступному:
Виберемо деякий елемент х масиву А випадковим способом;
Розглядаємо масив у прямому напрямку (і= 1, 2, ...), шукаючи у ньому елемент А[i] не менший, ніж х;
3.Розглядаємо масив у зворотному напрямку(j = n, n-1,..), шукаючи у ньому елемент A[j] не більший, ніж x;
4.Меняємо місцями A[i] і A[j];
Пункти 2-4 повторюємо до тих пір, поки i < j;
В результаті такого зустрічного проходу початок масиву A[1..i] і кінець масиву A[j..n] опиняються розділеними “бар’єром” x: A[k] £ x при k < i , A[k] ³ x при k > j , причому на розділ ми затратимо не більш n/2 перестановок. Тепер залишилось зробити ті ж дії з початком і кінцем масиву, тобто застосувати їх рекурсивно!
Таким чином, процедура Hoare, що описана нами, залежить від параметрів k і m - початкового і кінцевого індексів відрізку масиву, що оброблюється.
Procedure Swap(i, j : Integer);
Var
b : Real;
Begin
b := a[i];
a[i] := a[j];
a[j] := b
End;
Procedure Hoare(L, R : Integer);
Var
left, right : Integer;
x : Integer;
Begin
If L < R
then begin
x := A[(L + R) div 2]; {вибір бар’єру x}
left := L; right := R ;
Repeat {зустрічний прохід}
While A[left] < x do left := Succ(left); {перегляд уперед}
While A[right] > x do right := Pred(right); {перегляд назад}
If left <= right
then begin
Swap(left, right);
left := Succ(left);
right := Pred(right);
end
until left > right;
Hoare(L, right); {сортуємо початок}
Hoare(left, R) {сортуємо кінець}
end
End;
Program QuickSort;
Const
n = 100;
Var
A : array[1..n] of Integer;
{ процедури Swap, Hoare, введення Inp і виведення Out}
Begin
Inp;
Hoare(1, n);
Out
End.
Найбільш важливе місце алгоритму Хоара – правильне опрацювання моменту закінчення руху покажчиків left, right. Помітьте, що в нашій версії переставляються місцями елементи, що дорівнюють x. Якщо в циклах While замінити умови (A[left] < x) і (A[right] > x) на (A[left] <= x) і (A[right] >=x), при x = Max(A) індекси left і right пробіжать весь масив і побіжать далі! Ускладнення ж умов продовження перегляду погіршить ефективність програми.
Аналіз складності алгоритму в середньому, що використовує гіпотезу про рівну ймовірність всіх входів, показує, що
C(n) = O(n log2 n), M(n) = O(n log2 n).
У гіршому випадку, коли в якості бар’єрного вибирається, наприклад, максимальний елемент підмасиву, складність алгоритму квадратична.
10.5. Пошук k-того в масиві. Пошук медіани масиву
З задачею сортування тісно пов’язана задача находження k-того за величиною елемента у масиві. З її частковим випадком – пошук 1-го (мінімального) і n-того елемента (максимального) – ми вже знайомі. Аналогічно можна розв’язати задачу пошуку 2-го і (n - 1)-го за величиною елементів, однак кількість порівнянь зростає вдвічі. Перш, ніж розглянути задачу у загальному виді, приведемо необхідне визначення.
К-тим за величиною елементом послідовності називається такий елемент b цієї послідовності, для якого в послідовності існує не більш, ніж k-1 елемент, менший, ніж b і не менше k елементів, менше або рівних b.
Наприклад, у послідовності {2, 1, 3, 5, 4, 2, 2, 3 } четвертим за величиною буде 2.
Іншими словами, якщо відсортувати масив, то k-тий елемент опиниться на k-тому місці (b = A[k]). Можна очкувати, що найбільш складним буде алгоритм пошуку елемента при k = n div 2 – тобто елемента, рівновіддаленого від кінців масиву. Цей елемент назвемо медіаною масиву.
Очевидний розв’язок задачі пошуку k-того елемента – повне або часткове (до k) сортування масиву A. Наприклад, алгоритм TreeSort можна перервати після просівання k елементів. Тоді C(n) = O(n + k log2 n)
Однак ефективний на практиці розв’язок можна отримати, якщо застосувати ідею К.Хоара розділення масиву бар’єром. Насправді, аналіз метода розділення елементів по бар’єру в процедурі Hoare показує, що після її закінчення мають місце співвідношення
Right < Left, при i < Left A[i] <= x, при i > Right A[i] >= x
Таким чином, відрізок First .. Last розбиває на 3 частини:
First Right Left Last
A[i] <= x A[i] = x A[i] >= x
Подальший пошук, отже, можна організувати так:
Якщо k <= right
то шукати k-тий елемент в A[First .. right]
інакше якщо k <= left
то k-тий елемент дорівнює x
інакше шукати k - тий елемент в A[left + 1 .. Last]
Procedure HoareSearch(First, Last : Integer);
Var
l, r : Integer; x : Integer;
Begin
If First = Last
then Write(A[k]) { залишився 1 елемент }
else If First < Last
then begin
x := A[k]; {вибір бар’єра x}
l := First;
r := Last;
Repeat {зустрічний прохід}
While A[l] < x do l := Succ(l);
While A[r] > x do r := Pred( r );
If l <= r
then begin
Swap(l, r);
l := Succ(l);
r := Pred( r );
end
until l > r;
If k <= r
then HoareSearch(First, r) {1-а частина масиву}
else If k <= l
then Write(x) {елемент знайдений}
else HoareSearch(l+1, Last) {3-ая частина масиву}
end
End;
Як і алгоритм швидкого сортування, цей алгоритм у гіршому випадку неефективний. Якщо при кожному розділу 1-а частина масиву буде містити 1 елемент, алгоритм витратить O(k*n) кроків. Однак в середньому його складність лінійна (незалежно від k). Зокрема, навіть при пошуку медіани A[n div 2]
Ccр(n) = O(n), Mcр(n) = O(n)
10.6.* Метод “розділяй і володій”
Один з найбільш відомих методів проектування ефективних алгоритмів – метод “розділяй і володій” полягає у зведенні задачі, що розв’язується, до рішення однієї або кількох більш простих задач.
Якщо спрощення задачі полягає в зменшенні її параметрів, таке зведення дає рекурсивний опис алгоритму. Зокрема, зменшення параметра може означати зменшення кількості даних, з якими працює алгоритм.
Характерна ознака методу – зведення до декількох задач рівних за складністю підзадач. Ефективність отриманого алгоритму залежить від, по-перше, від кількості дій, затрачених на зведення задачі до підзадач, по-друге – від балансу складностей підзадач.
Класичний приклад застосування методу – бінарний пошук у впорядкованому масиві. Масив розбивається на дві рівні частини. Використовуючи потім два порівняння, алгоритм або знаходить елемент, або визначає ту половину, в якій його треба шукати – тобто зводить задачу розміром n до задачі розміром n/2. Цей же прийом використовується в алгоритмах Хоара сортування і пошуку, в алгоритмі піднесення числа в натуральну степінь, у деяких інших раніше сформульованих задачах. Розглянемо відомий розв’язок задачі пошуку мінімального і максимального елемента в масиві.
Нехай A[1..n] – числовий масив. Треба знайти Max(A) і Min(A). Припустимо, що n = 2 k. Таке припущення дає можливість завжди ділити масиви, отримані навпіл.
Опишемо основну процедуру MaxMin. Нехай S – деяка множина і |S| = m. Розіб’ємо S на рівні за числом елементів частини: S = S1 È S2, Знайдемо Max1, Min1 як результат MaxMin(S1) і Max2, Min2 як результат MaxMin(S2).
Потім Max := Max(Max1, Max2); Min := Min(Min1, Min2);
Procedure MaxMin(L, R : Integer Var Max, Min : Real);
Var
Max1, Min1, Max2, Min2 : Real;
Begin { L, R - межі індексів масиву A }
If R - L = 1
then If A[L] > A[R] { вибір Маx, Min за одне порівняння}
then begin
Max := A[l];
Min := A[R]
end
else begin
Max := A[R];
Min := A[L]
end
else begin
C := (R + L - 1) div 2;
MaxMin(L, C, Max1, Min1);
MaxMin(C+1, R, Max2, Min2);
If Max1 > Max2
then Max := Max1
else Max := Max2;
If Min1 < Min2
then Min := Min1
else Min := Min2
end
End;
Нехай С(n) - оцінка складності процедури MaxMin в термінах порівнянь. Тоді, очевидно
С(2) = 1,
C(n) = 2 C(n/2) + 2 при n > 2
Звідси С(n) = 2 (n/4 + n/8 + ... + 1) + n/2 = 2(n/2 - 1) + n/2;
C(n) = 3/2 n - 2
Для порівняння відзначимо, що алгоритм пошуку Max і Min методом послідовного перегляду масиву потребує 2n-2 порівнянь. Таким чином, застосування метода “розділяй і володій” зменшило часову складність задачі в фіксоване число раз. Зрозуміло, істинна причина поліпшення – не в застосуванні рекурсії, а в тому, що максимуми і мінімуми двох елементів масиву, що стоять поруч, відшукуються за одне порівняння! Метод дозволив просто і природно описати обчислення.
Довжина ланцюжка рекурсивних викликів в алгоритмі дорівнює log2 n -1, і в кожній копії використовується 4 локальних змінних. Тому алгоритм використовує допоміжну пам’ять об’єму O(log2 n), що розподіляється динамічно. Це – плата за економію часу.
10.7.* Метод цифрового сортування
Іноді при розв’язані задачі типу задачі сортування можна використовувати особливості типу даних, що перетворюються, для отримання ефективного алгоритму. Розглянемо одну з таких задач – задачу про обернення підстановки.
Підстановкою множини 1..n назвемо двомірний масив A[1..2, 1..n] виду
|
|
| ..........
| n-1
| n
|
| j1
| j2
| ...........
| j n-1
| j n
|
в якому 2-ий рядок містить всі елементи відрізка 1. .n. Підстановка B називається оберненою до підстановки A, якщо B отримується з A сортуванням стовпців A у порядку зростання елементів 2-ого рядка з наступною перестановкою рядків. Треба побудувати алгоритм обчислення оберненої підстановки. З визначення випливає, що стовпець [i, ji] підстановки A треба перетворити в стовпець [ji , i] і поставити на ji-те місце в підстановці B.
{
Type
NumSet = 1..n;
Substitution = array[ 1..2, NumSet] of NumSet;
}
Procedure Reverse ( Var A, B : Substitution);
Begin
For i := 1 to n do begin
B[A[2, i], 2] := i;
B[A[2, i], 1] := A[2, i]
end
End;
Складність процедури Reverse лінійна, оскільки тіло арифметичного циклу складається з двох операторів присвоювання. Між тим стовпці підстановки відсортовані.
Аналогічна ідея використовується в так званому сортуванні вичерпуванням (або цифровому сортуванні), що застосовується для сортування послідовностей слів (багаторозрядних чисел). Для кожної букви алфавіту алгоритм створює структуру даних “черпак”, в яку пересилаються слова, що починаються на цю букву. В результаті перегляду послідовність виявляється відсортованою по першій букві. Далі алгоритм застосовують рекурсивно до кожного “черпака”, сортуючи його по наступним буквах.
10.8. Задачі і вправи
1.Дано масив А[1..900] of 1..999. Знайти трьохзначне число, що не знаходиться у цьому масиві. Розглянути два варіанта задачі:
а) Допоміжні масиви в алгоритмі не використовуються;
б) Використання допоміжних масивів дозволено.
2.Реалізувати алгоритм TreeSort, застосувавши метод вкладення дерева в масив. Для цього використати допоміжний масив В.
3.Реалізувати ітеративну версію алгоритму HeapSort:
а)Замінити рекурсію в процедурі SortTree арифметичним циклом For...downto, що оброблює дерево за рівнями, починаючи з нижнього;
б)Замінити рекурсію в процедурі Conflict ітераційним циклом, керуючим змінною i. { i := 2i або i := 2i + 1 }.
4.Реалізувати ітеративну версію алгоритму процедури HoareSeach, замінивши рекурсію ітераційним циклом.
5-6. Застосувати для розв’язку задач 1-2 параграфа 8 ідею Хоара.
7.Реалізувати алгоритм “тернарного” пошуку елемента в упорядкованому масиві, поділяючи ділянку пошуку на 3 приблизно рівні частини. Оцінити складність алгоритму у термінах С (n). Порівняти ефективності бінарного і тернарного пошуку.
8.Реалізувати алгоритм пошуку максимального і мінімального елементів у масиві (процедура MaxMin) для довільного n.
9.Нехай A[1..n] - масив цілих чисел, упорядкований за зростанням (A[i] < A[i+1]). Реалізувати алгоритм пошуку такого номера і, що A[i]= і методом “розділяй і володій”. Оцінити складність алгоритму.
10-12. Застосувати для розв’язку задач 3-5 параграфа 8 метод “розділяй і володій”.
13.Реалізувати алгоритм процедури Reverse “на місці”, формуючи обернену підстановку в масиві А.
Задачі обчислювальної геометрії.
14. Дано набір з n точок площини, заданих координатами A1(X1, Y1), A2(X2, Y2) , ..., An(Xn, Yn). Знайти таку точку S(X, Y) на площині, сума відстаней від якої до даних точок набору найменша. Проілюструвати розв’язок на малюнку.
15. Дано набір з n точок площини, заданих координатами: A1(X1, Y1), A2(X2, Y2), ..., An(Xn, Yn). Вибрати з цього набору точки, що знаходяться в вершинах випуклого багатокутника найменшої площини і який містить всі точки набору. Проілюструвати розв’язок на малюнку.
16. Дано набір з n точок площини, заданих координатами: A1(X1, Y1), A2(X2, Y2), ..., An(Xn, Yn). Побудувати коло найменшого діаметра, який містить всі точки набору. Проілюструвати розв’язок на малюнку.
17. Дано набір з n точок площини, заданих координатами: A1(X1, Y1), A2(X2, Y2), ..., An(Xn, Yn). Побудувати прямокутник найменшої площини, який містить всі точки набору. Проілюструвати розв’язок на малюнку.
18. Випуклий n-кутник заданий набором вершин
A1(X1, Y1), A2(X2, Y2), ..., An(Xn, Yn).
Розбиття цього багатокутника на трикутники діагоналями, що не перетинаються називається тріангуляція. Вартістю тріангуляції називається сума довжин діагоналей розбиття. Знайти тріангуляцію багатокутника найменшої вартості. Проілюструвати розв’язок на малюнку.
11. СКЛАДНІ ТИПИ ДАНИХ: ЗАПИСИ І ФАЙЛИ
11.1. Складні типи даних у мові Pascal
Ми вже отримали уявлення про деякі типи даних, які використовуються при програмуванні на Паскалі. Прості типи даних або заздалегідь визначені як стандартні, або визначаються в програмі.
Стандартні типиТипи, що визначаються програмістом
Integer; Тип, що перераховується;
Real; Скалярний тип.
Char:
Boolean.
З поняттям простого типу пов’язані:
· ім’я типу;
· множина допустимих значень типу;
· набір операцій, що визначені на типі;
· набір відношень, що визначені на типі;
· набір функцій, що визначені або набувають значення на типі.
З даних простих типів можна конструювати дані складних типів. Єдиним (поки) прикладом складних типів є регулярні типи (значення - масиви). З поняттям складного типу пов’язані:
* ім’я типу;
* спосіб об’єднання даних у дане складного типу;
* спосіб доступу до даних, що утворюють складне дане типу;
Так, визначення
Type
Vector = array [1..N] of Integer;
Var
X : Vector;
задає N цілих чисел, що об’єднані в єдине ціле - масив з іменем Х. Доступ до компоненти масиву здійснюється за його іменем Х і значенням індексного виразу: X[i].
Крім регулярних типів, у мові визначені ще деякі складні типи. Кожне таке визначення задає свій, характерний механізм об’єднання даних у єдине ціле і механізм доступу до даних – компонент складного даного.
Це - комбінований тип (записи), файловий тип (файли), множинний тип (множини) і посилальний тип (посилання).
11.2. Записи
Значеннями так званого комбінованого типу даних є записи. Комбінований тип задає образ структури об’єкта – даного цього типу, кожна частина якого (поле) може мати зовсім різні характеристики.
Таким чином, запис – це набір різнотипних даних, що об’єднані спільним іменем. Більш формально, запис містить визначене число компонент, що називаються полями.
У визначенні типу запису задається ім’я і тип кожного поля запису:
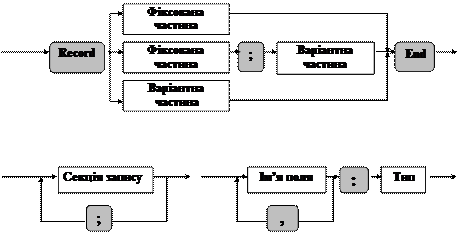
<комбінований тип >::= Record
< список полів >
End
<список полів>::= <фіксов. част.> | <фіксов. част.>;
<варіант. част.> | <варіант. част.>
<фіксована частина >::= <секція запису > {,<секція запису >}
< секція запису >::= <ім’я поля >{,<ім’я поля >}:< тип > < пусто >
Синтаксис записів, що містять варіантну частину – записів з варіантами – ми визначимо нижче. Відповідні синтаксичні діаграми записів з варіантами:


 a2 = min(a1,a2)
a2 = min(a1,a2)