Тіло циклу Repeat виконується до тих пір, поки умова приймає значення False. Дії, що містяться в тілі циклу, будуть виконані у крайньому випадку один раз. Таким чином, умова є умовою закінчення циклу.
Приклад 8.2. Знайти номер найменшого числа Фібоначчі, що ділиться на 10. Послідовність Фібоначчі { F(n) } визначається рекурентно:
F(1) = F(2) = 1, F(n+2) = F(n+1) + F(n)
Як і у попередньому прикладі, обчислюємо Fn для n = 3, 4, ... до тих пір, поки не знайдемо елемент послідовності, що ділиться на 10. Проблема обґрунтування методу залишається тією ж: чи існує потрібний елемент?
Program Fibbonachy;
Var
Fib1, Fib2 : Integer;
Index : Integer; Buf : Integer;
Begin
Fib1 := 1;
Fib2 := 1;
Index := 2; { Ініціалізація циклу }
Repeat
Buf := Fib2;
Fib2 := Fib2 + Fib1; { Наступне число Фібоначчі }
Fib1 := Buf; { Попереднє число Фібоначчі }
Index := Succ(Index) { Номер числа Фібоначчі }
until Fib2 mod 10 = 0;
Writeln(‘Номер = ‘, Index, ‘ Число = ‘, Fib2)
End.
Цикли While і Repeat називають ще ітераційними циклами, оскільки за їх допомогою легко реалізувати різного роду ітераційні обчислення (обчислення, в яких кожний наступний результат є уточненням попереднього). Умова закінчення циклу – досягнення відхилення результату Yn от Yn-1 деякої допустимої похибки e:
|Yn - Yn-1| < e
Приклад 8.3: Обчислити з заданою точністю значення кореня рівняння x = cos(x) на відрізку [0 ; 1] методом ділення відрізка навпіл .
Метод наближеного розв’язування рівняння діленням відрізка навпіл – один з найбільш простих і поширених чисельних методів. Суть його полягає у послідовному уточненні меж відрізка, на якому існує корінь. На кожному кроці методу цей відрізок ділиться навпіл, а потім вирішується питання про те, в якій половині (лівій чи правій) знаходиться корінь. Зменшення відрізка вдвоє теоретично гарантує завершення циклу пошуку з заданою точністю.
Procedure TransEquation (a, b, Epsilon : Real; Var Root: Real);
Var
u, v: Real;
Fu, Fr : Real;
Begin
u := a;
v := b; { ініціалізація циклу}
Fu := Cos(u) - u;
Repeat
Root := (u + v)/2 ; { середня точка відрізка }
Fr := Cos(Root) - Root;
if Fu*Fr > 0 { вибір правої або лівої половини }
then begin
u := Root;
Fu := Fr
end
else v := Root
until Abs(v - u) < Epsilon;
End;
Для того, щоб знайти кількість N повторень у циклі, відмітимо, що на k-тому кроці циклу виконана нерівність |v - u| = (b - a)/2k. Тому при найменшому k такому, що (b - a)/2k < e цикл завершиться. Неважко обчислити N:
N = [ log2(b - a)/ e] (1)
Як показують розглянуті приклади, одна з основних проблем аналізу програм, що містять ітераційні цикли, складається в обґрунтуванні завершення циклу (і програми). На відміну від алгоритмів з арифметичними циклами, ця проблема не є простою!
Оскільки кількість повторень ітераційного циклу не визначена, задача оцінки складності програми часто також не проста.
8.2. Алгоритми пошуку і сортування. Лінійний пошук у масиві
Приклад 8.4. Розглянемо красивий розв’язок задачі пошуку даного елемента в масиві, що використовує цикл While. Насправді, замість використання циклу For з достроковим виходом при допомозі Goto можна застосувати цикл While:
Program WhileSearch;
Const
n = 100;
Type
Vector = array[1..n] of Real;
Var
A : Vector ;
b : Real;
Procedure InpMas(Var V : Vector);
Var i : Integer;
Begin
For i := 1 to n do begin
Write(‘Введіть елемент масива : ‘);
Readln(V[i]);
end;
End;
Procedure InpData(Var b:Real);
Begin
Write(‘Введіть шукане значення : ‘);
Readln(b)
End;
Procedure Found (Var A : Vector; b : Real);
Var i : Integer;
Begin
i := 1;
While (i <= n) and (A[i] <> b) do i := Succ(i);
If i = n + 1
then Writeln(‘Елемент ‘,b,’у масиві відсутній’)
else Writeln(‘елемент ‘,b, розміщений на’,i,’-тому місці’);
End;
Begin
{Блок читання масиву A і елемента b}
InpMas(A);
InpData(b);
Found (A, b);
End.
Недоліком такої реалізації є по-перше, використання складеної умови в циклі, по-друге – можливо некоректне обчислення підвиразів A[i] <> b при i = n +1. Не дивлячись на те, що умова є хибною (i <= n = False), вираз A[n+1] <> b не визначено!
Доповнимо масив A ще одним елементом: A[n+1] = b, і всі недоліки легко ліквідуються!
Program LinearSearch;
Const
n = 101; { Розмір масиву збільшений на 1 }
Type
Vector = array[1..n] of Real;
Var
A : Vector ;
b : Real;
Procedure InpMas(Var V : Vector);
Var i : Integer;
Begin
For i := 1 to n-1 do begin
Write(‘Введіть елемент масива : ‘);
Readln(V[i]);
end;
End;
Procedure InpData(Var b:Real);
Begin
Write(‘Введіть шукане значення : ‘);
Readln(b)
End;
Procedure Found (Var A : Vector; b : Real);
Var i : Integer;
Begin
i := 1;
A[n] := b; { Доповнимо масив “бар’єрним” елементом }
While A[i] <> b do i := Succ(i);
If i = n
then Writeln(‘Елемент ‘,b,’в масиві відсутній’)
else Writeln(‘елемент ‘,b,’розміщений на’,i,’-тому місці’);
End;
Begin
{Блок читання масиву A і елемента b}
InpMas(A);
InpData(b);
Found (A, b);
End.
8.3. Поліпшений алгоритм сортування обмінами
Приклад 8.5. У програмі BublSort цикл For використовується в якості зовнішнього. Це приводить до того, що він виконується рівно n - 1 разів, навіть якщо масив вже упорядкований після декількох перших проходів. Від зайвих проходів можна позбавитися, застосувавши цикл Repeat і перевіряючи у внутрішньому циклі масив на упорядкованість:
Procedure BublSort1 (Var a:Vector);
Var
i, j : Integer;
Temp : Real;
isOrd : Boolean;
Begin
i := n - 1;
Repeat
isOrd := True; { ознака упорядкованості}
For j := 1 to i do
If a[j] > a[j+1]
then begin
Temp := a[j+1];
a[j+1] := a[j];
a[j] := Temp;
isOrd := False { виявлено“засортування” }
end;
i := Pred(i)
until isOrd;
End;
Цей алгоритм можна ще покращити, якщо кожний наступний прохід починати не з початку (j = 1), а з того місця, де на попередньому проході відбувся перший обмін:
{LowIndex : Integer;}
Repeat
isOrd := True; { ознака упорядкованості}
LowIndex := 1; { відрізок A[1..LowIndex] упорядкований}
For j := LowIndex to i do
If a[j] > a[j+1]
then begin
Temp := a[j+1];
a[j+1] := a[j];
a[j] := Temp;
If isOrd then begin
LowIndex := j;
isOrd := False
end
end;
i := Pred(i)
until isOrd;
Відзначимо однак, що наш алгоритм працює не симетрично: якщо найбільший елемент “спливає” на своє місце за один прохід, то найменший елемент “потоне” на 1-е місце, знаходячись початково на n-тому місці, за n-1 прохід. При цьому здійсниться максимально можливе число порівнянь. Усунути асиметрію можна, чергуючи проходи вперед і назад. Реалізацію цієї ідеї, як і подальші поліпшення алгоритму сортування простими обмінами, ми надаємо читачеві в якості вправи.
Всі поліпшення методу, що розглядається відносяться до ефективності в середньому. Жодне з них не зменшує оцінки складності С (n) у гіршому випадку.
8.4. Бінарний пошук в упорядкованому масиві
Приклад 8.6. Задача пошуку суттєво спрощується, якщо елементи масиву упорядковані. Стандартний метод пошуку в упорядкованому масиві – це ділення відрізка навпіл, причому відрізком є відрізок індексів 1..n. Насправді, нехай m (k < m < l) – деякий індекс. Тоді якщо A[m] > b, далі елемент треба шукати на відрізку k..m-1, а якщо A[m] < b - на відрізку m+1..l.
Для того, щоб збалансувати кількість обчислень в тому і іншому випадках, індекс m треба вибирати так, щоб довжини відрізків k..m, m..l були (приблизно) рівними. Описану стратегію пошуку називають бінарним пошуком.
Procedure BinarySearch (Var A: Vector; b : Real; Var m: Integer);
Var
Buf : Real;
k, l : Integer;
Begin
k := 1; l := n;
Repeat
m := (k + l) div 2;
Buf := A[m];
If Buf > b
then l := Pred(m)
else k := Succ(m)
until (Buf = b) or (l < k);
If A[m] <> b
then m:=0;
End;
Якщо елемент не знайдено, процедура повертає значення індексу рівне нулю.
Неважко отримати оцінку числа С (n) порівнянь методу, застосувавши формулу (1) прикладу 8.3. Нехай М - кількість повторень циклу. Тоді
М £ [log2 (n)]
Оскільки на кожному кроку здійснюється 2 порівняння, у гіршому випадку
C(n) = 2[log2 n] = O(log2 n) (2)
8.5. Алгоритми сортування масивів (продовження). Сортування вставками
Ще один простий алгоритм сортування - сортування вставками базується на наступній ідеї: припустимо, що перші k елементи масиву A[1..n] вже упорядковані:
A[1] £ A[2] £ ... £ A[k], A[k+1], ..., A[n]
Знайдемо місце елемента A[k+1] в початковому відрізку A[1],...,A[k] і вставимо елемент на своє місце, отримавши упорядковану послідовність довжини k+1. Оскільки початковий відрізок масиву упорядкований, пошук треба реалізувати як бінарний. Вставці елемента на своє місце повинна передувати процедура зсуву “хвоста” початкового відрізка для звільнення місця.
Program InsSort;
Const
n = 100;
Type Vector = array[1..n] of Integer;
Var
A : Vector
Procedure BinFind( Var A: Vector; b, k: Integer; Var j: Integer);
Var l, r, i : Integer;
Begin {Бінарний пошук}
l := 1;
r := k;
Repeat
j := (l + r) div 2;
If b < A[j]
then r := j
else l := j + 1;
until (l = j);
End;
Procedure Sort( Var A: Vector);
Var k, b, j, i : Integer;
Begin
For k := 1 to n-1 do begin
b := A[k+1];
If b < A[k]
then begin
BinFind(A, b, k, j );
For i := k downto j do A[i+1] := A[i]; {Зсув частини масиву на 1 праворуч}
A[j] := b ; { Пересилання елемента на своє місце}
end
end;
End;
Begin
{Блок читання масиву A}
Sort(A);
{Блок виведення масиву A}
End.
8.5.1 * Ефективність алгоритму
Оцінимо ефективність алгоритму. Пошук міста елемента A[k+1] потребує, як показано вище, O(log2 k ) порівнянь. Тому у гіршому випадку кількість порівнянь С (n) є
C(n) = O(log2 2 ) + ... + O(log2(n-1)) + O(log2 n) = O(n log2 n)
Зсув правої частини масиву на кожному кроці зовнішнього циклу у гіршому випадку потребує k перестановок. Тому у гіршому випадку
M(n) = 1 + ... + (n-2) + (n-1) = n*(n-1)/2 = O(n2)
Таким чином, алгоритм сортування вставками значно ефективніший, ніж всі розглянуті раніше алгоритми за числом порівнянь. Однак число перестановок у гіршому випадку також буде значним, як і у самому неефективному алгоритмі – сортуванню простими обмінами.
8.6. Задачі і вправи
1. Визначити число членів нескінченного ряду чисел, необхідне для обчислення його суми з точністю e.
¥
а. S [(-1)n /(2n+1)] = p/4
n=0
¥
б. S [(-1)n/(2n)!] = cos 1
n=0
¥
в. S [(-1)n/(2n+1)!] = sin 1
n=0
2. Знайти суму членів ряду з заданою похибкою e.
¥
а. sin x = S (-1)n(x2n+1)/(2n+1)!
n=0
¥
б. ln x = S (-1)n*xn / n; x>1/2
n=1
¥
в. arctg x = S (-1)n x2n+1/(2n+1); |x|<1
n=0
3. Знайти всі трьохзначні члени послідовності Fn, визначеної рекурентними співвідношеннями:
а. F0 = 1, F1 = 1,
Fn+2 = Fn+1 + Fn при n > 0
б. F0 = 5, F1 = 1, F2 = 1,
Fn+3 = Fn+2 + Fn+1 - Fn при n > 0
4. Дано раціональне число p/q. Побудувати його розклад у ланцюговий дріб.
5. Побудувати розклад натурального числа N у добуток степенів його простих дільників.
6. Перевести ціле число N у 2-ічну систему числення. Узагальнити алгоритм на випадок p-ічної системи числення.
7. Відомо, що якщо d = НСД(a,b), то існують такі числа u, v, що d = au + bv. По даним a, b знайти d, u, v.
8. Число N називається досконалим, якщо воно співпадає з сумою своїх власних дільників. (Наприклад, 6=1+2+3). Знайти всі досконалі числа, які не перевищують М.
9. Знайти номер найменшого числа Фібоначчі, що закінчується 2-ма нулями. Знайти саме це число.
10. Дано масив A[1..n] дійсних чисел. Знайти у цьому масиві найменше додатне число.
11. Дано масив A[1..n] цілих чисел. Знайти в цьому масиві найбільшу кількість нулів, що йдуть підряд.
12. Дано масив A[1..n] цілих чисел. Відрізок індексів k .. m називається відрізком росту масиву, якщо A[k] < A[k+1] < ... < A[m]. Знайти відрізок росту максимальної довжини.
13. Масив A[1..n] складається з даних типу Color = (white, black). Скласти програму сортування масиву A, яка перевіряє значення (колір) кожного елемента тільки один раз.
14. Масив A[1..n] складається з даних типу Color = (white, red, black). Скласти програму сортування масиву A, яка перевіряє значення (колір) кожного елемента тільки один раз.
15. Масив A[1..n] складається з дійсних чисел, причому для будь-якого 2 £ i £ n-1 виконана нерівність A[i] £ (A[i-1] + A[i+1])/2 Скласти програму пошуку найменшого і найбільшого елементів масиву, складність якої C(n) = O(log2(n))
16. Задані упорядковані масиви A[1..n] і B[1..m] цілих чисел і ціле число C. Скласти програму пошуку таких індексів i і j, що C = A[i] + B[j], складність якої C(n) = O(log2(n m))
17. Множина точок площини {Ai = ( Xi, Yi )} задана масивами координат X[1..n] і Y[1..n]. Випуклою лінійною оболонкою цієї множини називається така його підмножина В, що багатокутник з вершинами в точках з В є випуклими і містить всю множину А. Скласти програму пошуку випуклої лінійної оболонки множини А. Оцінити її складність.
9. РЕКУРСІЯ
9.1. Рекурсивно-визначені процедури і функції
Описання процедури А, в розділі операторів якої використовується оператор цієї процедури, називається рекурсивним. Таким чином, рекурсивне описання має вид
Procedure A(u, v : ParType);
...
Begin
...; A(x, y); ...
End;
Аналогічно, описання функції F, в розділі операторів якої використовується виклик функції F, називається рекурсивним. Рекурсивне описання функції має вид
Function F(u, v : ArgType) : FunType;
...
Begin
...; z := g(F(x, y)); ...
End;
Використання рекурсивного описання процедури (функції) приводить до рекурсивного виконання цієї процедури (обчислення цієї функції). Задачі, що формулюються природним чином як рекурсивні, часто приводять до рекурсивних розв’язків.
Приклад 9.1. Факторіал.
Розглянемо рекурсивне визначення функції n!=1*2*...*n (n-факторіал). Нехай F(n) = n! Тоді
1.F(0) = 1
2.F(n) = n*F(n - 1) при n > 0
Засобами мови це визначення можна сформулювати як обчислення:
If n = 0
then F := 1
else F := F(n - 1) * n
Оформивши це обчислення як функцію і змінивши ім’я, отримаємо:
Function Fact(n: Integer): Integer;
Begin
If n = 0
then Fact := 1
else Fact := Fact(n - 1) * n
End;
Обчислення функції Fact можна представити як ланцюжок викликів нових копій цієї функції з передачею нових значень аргументу і повернень значень функції в попередню копію.
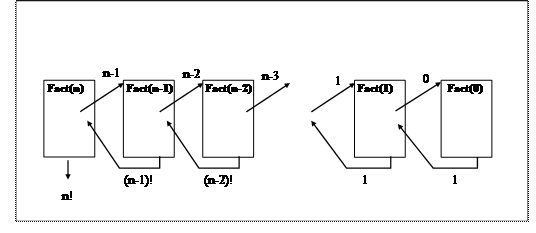

Ланцюжок викликів обривається при передачі нуля в нову копію функції. Рух у прямому напрямку (розгортання рекурсії) супроводжується тільки обчисленням умови і викликом. Значення функції обчислюється при згортанні ланцюжка викликів. Складність обчислення Tfact(n) функції Fact можна оцінити, виписавши рекурентне співвідношення:
Tfact(n) = Tfact(n-1) + Tm + Tl + Tс
Для того, щоб обчислити Tfact(n), треба здійснити одну перевірку, одне множення і один виклик Tfact(n-1). Виклик Tfact потребує затрат часу Tc на “адміністративні” обчислення: передачу параметра, запам’ятовування адреси повернень і т.п. Поклавши С = Tm+Tl+Tс, отримаємо Tfact(n) = Tfact(n-1) + С. Неважко тепер показати, що Tfact(n) = Сn.
Приклад 9.2. Перестановки. Згенерувати всі перестановки елементів скінченої послідовності, що складається з букв.
Спробуємо звести задачу до декількох підзадач, більш простих, ніж вихідна.
Нехай S = [ s1, s2, ..., sn ] - набір символів.
Через Permut(S) позначимо множину всіх перестановок S, a через Permut(S,i) - множину всіх перестановок, в яких на останньому місці стоїть елемент si. Тоді
Permut(S) = Permut(S,n) È Permut(S, n-1) È ... È Permut(S,1)
Елемент множини Permut(S, i) має вид [sj2,..., sjn,si] де j2,..., jn - всі можливі перестановки індексів, не рівних I. Тому Permut(S, i) = (Permut(S \ si), si) і Permut(S)=(Permut(S \ s1),s1)+...+ (Permut(S \ sn), sn).
Отримане співвідношення виражає множину Permut(S) через множини перестановок наборів з (n-1) символу. Доповнивши це співвідношення визначенням Permut(S) на одноелементній множині, отримаємо:
1. Permut({s}) = {s}
2. Permut(S) = (Permut(S\s1), s1) + ... + (Permut(S\sn), sn)
Уточнимо алгоритм, опираючись на представлення набору S в виді масиву S[1..n] of char.
По перше, визначимо параметри процедури Permut:
k - кількість елементів в наборі символів;
S - набір символів, що переставляються.
Алгоритм починає роботу на вхідному наборі і генерує всі його перестановки, що залишають на місці елемент s[k]. Якщо множина перестановок, в яких на останньому місці стоїть s[j], уже породжена, міняємо місцями s[j-1] і s[k], виводимо на друк отриманий набір і застосовуємо алгоритм до цього набору. Параметр k керує рекурсивними обчисленнями: ланцюжок викликів процедури Permut обривається при k = 1.
Procedure Permut(k : Integer; S : Sequence);
Var
j : integer;
Begin
if k <> 1
then Permut(k - 1, S);
For j := k - 1 downto 1 do begin
Buf := S[j];
S[j] := S[k];
S[k] := Buf;
WriteSequence(S);
Permut(k - 1, S)
end
End;
Begin { Розділ операторів програми}
{Генерація вихідного набору S}
WriteSequence(S); {Виведення першого набору на друк}
Permut(n, S)
End.
Оцінимо складність алгоритму за часом у термінах C(n): Кожний виклик процедури Permut(k) містить k викликів процедури Permut(k-1) і 3(k-1) пересилання. Кожний виклик Permut(k-1) супроводжується передачею масиву S як параметра-значення, що за часом еквівалентне n пересиланням. Тому мають місце співвідношення
C(k) = kC(k-1) + nk + 3(k-1), C(1) = 0, звідки С(n) = (n+3)n!
Оцінимо тепер розмір пам’яті, необхідної для алгоритму. Оскільки S - параметр-значення, при кожному виклику Permut резервується n комірок (байтів) для S, а при виході з цієї процедури пам’ять звільняється. Рекурсивне застосування Permut призводить до того, що ланцюжок вкладених викликів має максимальну довжину (n - 1):
Permut(n) --> Permut(n-1) --> ... --> Permut(2) --> Permut(1)
Тому дані цього ланцюжка потребують n2 - n комірок пам’яті, тобто алгоритм потребує пам’ять розміром O(n2). Кількість перестановок – елементів множини Рermut(S) дорівнює n!. Тому наш алгоритм “витрачає” C(n)/n! = O(n) дій для породження кожної перестановки. Зрозуміло, такий алгоритм неможна називати ефективним. (Інтуїція нам підказує, що ефективний алгоритм повинен генерувати кожну перестановку за фіксовану, незалежну від n кількість дій.) Джерело неефективності очевидне: використання S як параметра-значення. Це дозволило нам зберегти незмінним масив S при поверненні з рекурсивного виклику для того, щоб правильно переставити елементи, готуючи наступний виклик.
Розглянемо інший варіант цього алгоритму. Використаємо S як глобальну змінну. Тоді при виклику Рermut S буде змінюватись. Отже, при виході з рекурсії масив S треба поновлювати, використовуючи обернену перестановку!
Program All_permutations;
Const
n = 4;
Type
Sequence = array[1..n] of char;
Var
S : Sequence;
Buf : char;
i : Integer;
Procedure WriteSequence;
begin
For i := 1 to n do Write(S[i]);
Writeln
end;
Procedure Permut(k : Integer);
Var
j : integer;
Procedure Swap(i, j : Integer);
begin
Buf := S[j];
S[j] := S[i];
S[i] := Buf
end;
Begin
if k > 1
then Permut(k - 1);
For j := k - 1 downto 1 do begin
Swap(j, k); {Пряма перестановка}
WriteSequence;
Permut(k - 1);
Swap(k, j) {Обернена перестановка}
end
End;
Begin
{Генерація вихідного набору S}
WriteSequence; Permut(n)
End.
Тепер оцінка C(n) виходить з співвідношень
C(k) = kC(k-1) + 3(k-1), C(1) = 0 , т.е. C(n) = O(n!)
Цікаво, що цей варіант не потребує і пам’яті розміру O(n2) для збереження масивів. Необхідна тільки пам’ять розміру O(n) для збереження значення параметра k.
9.2. Приклади рекурсивних описів процедур і функцій
Декілька прикладів рекурсивних процедур, розглянутих у цьому пункті, допоможуть кращому засвоєнню техніки застосування рекурсії. Ми також побачимо переваги і недоліки рекурсивних описів.
Приклад 9.3. Повернені послідовності.
Розглянемо послідовність V(n), що задана рекурентно:
1.V(0) = V0, V(1) = V1, ..., V(k) = Vk;
2.V(n+k) = F( V(n+k-1), ... V(n+1), V(n), n )
Таке визначення задає послідовність V(n) фіксуванням перших її декількох членів і функції F, що обчислює кожний наступний член, виходячи з попередніх. Рекурентне визначення “дослівно переводиться” в функцію, що обчислюється рекурсивно:
Function V(n: Integer) : Integer;
Begin
Case n of
0: V := V0;
. . . . .
k: V := Vk
else V := F(V(n+k-1), ... V(n+1), V(n), n)
end
End;
Один з прикладів повернених послідовностей – послідовність Фібоначчі, програму обчислення якої ми вже розглядали. Ось її рекурсивна версія:
Function RF(n: Integer) : Integer;
Begin
Case n of
0,1: RF := 1
else RF := RF(n-1) + RF(n-2)
end
End;
Нажаль, це рішення вкрай неефективне: Можна довести, що
Tr f (n) > 2 n-2 при n>5.
Таким чином, складність обчислення RF(n) експоненціальна. Складність же ітеративного алгоритму обчислення Fib лінійна. У загальному випадку ситуація точно така ж: можна побудувати ітеративний алгоритм обчислення поверненої послідовності лінійної складності, рекурсивна ж версія при k>=1 має експоненціальну складність.
Приклад 9.4. Ханойські башти
Класичний приклад застосування рекурсії для описання ефективного алгоритму – задача про ханойські башти. На перший з трьох стержнів, закріплених вертикально на підставці, насаджено декілька кілець різних діаметрів так, що кільце меншого діаметра лежить на кільці великого діаметра. Два інших стержня порожні (рис. 9.1).
У задачі треба переставити всі кільця з 1-го стержня на 2-ий за декілька кроків. Кожний крок – це перестановка верхнього кільця одного стержня на верхнє кільце іншого стержня з дотриманням правила: діаметр кільця, що переставляється повинен бути менше, ніж діаметр кільця, на яке здійснюється перестановка.
Рис. 9.1

Нехай N – кількість кілець на стержні, І – номер кільця, з якого здійснюється перестановка і J – номер кільця, на який кільця треба переставити. Змінні N,I,J - параметри процедури HanojTower, керуючої перестановками. Крок розв’язку – процедура Step з параметрами I, J.
HanojTower (N,I,J) - процедура, що переставляє N кілець з I-того стержня на J-тий.
Step (I, J) - процедура , що переставляє 1-не кільце з I-того стержня на J-тий.
Відмітимо, що якщо I і J - номера 2-стержней, то 6-I-J - номер третього стержня.
Припустимо, що ми перемістили N-1 кільце з I-того стержня на 6-I-J стержень. (рис. 9.2)
Рис. 9.2
 (n-1) кільце
(n-1) кільце





 (n-1) кільце
(n-1) кільце