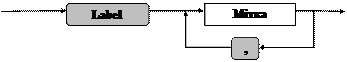Тут
Ім’я – це ім’я змінної - параметра циклу;
А – початкове значення параметра циклу;
В – кінцеве значення параметра циклу;
Оператор – тіло циклу.
Параметр циклу, початкове і кінцеве значення повинні бути одного й того ж скалярного типу (крім дійсного). Початкове і кінцеве значення обчислюються лише один раз – при вході в цикл, і, отже, повинні бути визначені до входу в цикл і не можуть бути змінені в тілі циклу.
Якщо початкове і кінцеве значення розділяє службове слово to, то після виконання оператора (тіло циклу) параметр циклу v приймає значення Succ(v), якщо ж між початковим і кінцевим значенями поставити downto, то параметр циклу v після виконання тіла циклу приймає значення Pred(v). Зокрема, якщо параметр v має тип Integer, то одночасно з виконанням тіла циклу здійснюється або присвоювання v := v + 1 (to), або v := v - 1 (downto). Додатково змінювати значення параметра в тілі циклу не рекомендується, оскільки контроль за правильністю виконання такого циклу є дуже складним. Якщо в циклі з to початкове значення більше, ніж кінцеве, то цикл не виконується взагалі. Аналогічно, якщо в циклі з downto початкове значення менше, ніж кінцеве, цикл також не виконується.
Стандарт мови локалізує дію параметра тільки в самому циклі, тому при нормальному виході з циклу, тобто коли параметр циклу вже прийняв всі можливі значення між початковим і кінцевим значеннями, значення параметра вважається невизначеним (В реалізації мови це правило часто не виконується).
Приклад 7.1. Знаходження факторіалу натурального числа.
Program NFactorial;
var
Argument: Integer;
Procedure InpData (Var Argument: Integer);
Begin
Write(‘ введіть аргумент факторіала ‘);
Readln(Argument) ;
End;
Function Fact(Argument: Integer): Integer;
Var Factorial, i : Integer;
Begin
Factorial := 1;
For i := 2 to Argument do Factorial := i*Factorial;
Fact:= Factorial;
End;
Begin
InpData (Argument);
Writeln(Argument,’! = ‘, Fact (Argument))
End.
У цьому прикладі
i - параметр циклу;
2 - початкове значення параметра циклу;
Argument - кінцеве значення параметра циклу;
Factorial := i*Factorial - тіло циклу.
Відмітимо, що на вході Argument > 7 значення Factorial вийде за межі типу Integer і результат буде неправильним.
¥ ¥
В наступному прикладі обчислюються суми S xn/n2, S xn/n3
n=0 n=0
Приклад 7.2.
Program SeriesSumma;
Var
Sum1, Sum2, x : Real;
Index, n : Integer;
Procedure InpData (Var x : Real; Var n: Integer);
Begin
Write(‘ введіть x і n ‘);
Readln(x, n); {Ініціалізація змінних, що використовуються в циклі}
End;
Procedure Sum (x : Real; n: Integer; Var Sum1, Sum2: Real);
Var Index: Integer;
u1, u2 : Real;
v : Real;
Begin
Sum1 := 1;
Sum2 := 1; { суми рядів }
v := 1; { x^n }
For Index := 1 to n do begin
v := v*x;
u1 := v/Sqr(Index);
u2 := u1/Index;
Sum1 := Sum1 + u1;
Sum2 := Sum2 + u2;
end;
End;
Begin
InpData (x, n);
Sum (x , n, Sum1, Sum2);
Writeln( ‘ S1 = ‘, Sum1,’ ‘,’ S2 = ‘, Sum2)
End.
Зверніть увагу на те, що всі оператори, які необхідно виконувати в циклі, об’єднані у складений оператор.
Часто крок зміни змінної, яка управляє циклом, відрізняється від 1, -1. Наступний приклад демонструє використання циклу з параметром у таких обчисленнях.
Приклад 7.3. Табулювання функції дійсної змінної.
Рrogram Tabulation;
const
Pi=3.14159262;
var
MinX, MaxX, Step: Real;
Procedure InpData (Var MinX, MaxX , Step: Real);
Begin
Write(‘Введіть межі табулювання ‘);
Readln(MinX, MaxX);
Write(‘Введіть крок табулювання ‘);
Readln(Step);
End;
Procedure Tabul(Var MinX, MaxX , Step: Real );
x, y : Real;
Coef : Real;
i, n : Integer;
Begin
n := Round((MaxX - MinX)/Step);
x := MinX;
Coef := 1/Sqrt(Pi);
for i := 0 to n do begin
y := Coef * exp(-Sqr(x)/2);
writeln(‘ x = ‘,x,’ y = ‘,y);
x := x + Step
end;
End;
Begin
InpData (MinX, MaxX , Step);
Tabul(MinX, MaxX , Step);
End.
Програма табулює функцію y=1/p*exp(-x2/2) в інтервалі значень [MinX, MaxX] з кроком Step. Зверніть увагу на те, що перед входом у цикл обчислюється N - верхня межа параметра циклу, а в тілі циклу обчислюється наступне значення х.
Приклад 7.4.
program Alfabet;
Var
Letter : char;
Begin
For Letter := ‘z’ downto ‘a’ do Write(Letter, ‘,’)
End.
7.2. Циклічні програми. Складність циклічної програми. Оптимізація циклічних програм
Циклічними називають програми, що містять оператори циклів. Циклічна програма може містити декілька операторів циклу, що виконуються послідовно або входять в інші оператори. Найпростіші циклічні програми містять один оператор циклу і оператори, що керують введенням-виведенням. До найпростіших відносяться циклічні програми розглянутих прикладів.
Складність Тц найпростішої циклічної програми, що містить арифметичний цикл, визначається формулою Tц = NTb де N - кількість повторень циклу, Tb - складність тіла циклу. Якщо арифметичний цикл завершується нормально, то N = |Ord(MaxVal) - Ord(MinVal)|, де MaxVal, MinVal – нижня і верхня межі параметра. Таким чином, оптимізація програми за часом полягає у зменшенні складності тіла циклу і (якщо це можливо) зменшенні кількості повторень циклу.
Для оптимізації тіла циклу використовують наступні прийоми:
Попереднє (поза циклу) обчислення підвиразів, значення яких не змінюється в циклі. Наприклад, у програмі Tabulation до входу в цикл обчислено значення Coef=1/Sqrt(Pi);
Використання співвідношень, що зв’язують змінні, які змінюються в циклі, для обчислень однієї з них через інші. У програмі SeriesSumma змінні u1 і u2 - члени ряду - визначені як функції від х, і:
u1(x, i) = xi / i2; u2(x, i) = xi / i3;
Тому має місце рівність u2*i = u1, яка використовується для обчислення u2.
7.3. Обмежені типи
Обмежений тип у мові Паскаль можна визначити, накладаючи обмеження на вже визначений скалярний тип – його називають базовим скалярним типом. Обмеження визначаються діапазоном – мінімальним і максимальним значеннями констант базового скалярного типу. Обмеження стандартного типу Real не допускається.
Синтаксична діаграма обмеження має вид:
 Обмежений
Обмежений
Тип
Наприклад:
а) Type
Day = 1..30; - обмеження на тип integer;
б) Digit = ‘0’..’9’; - обмеження на тип char;
в) Type
Weekday = (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday);
Workday = Monday..Friday; - обмеження на скалярний тип Weekday.
Базовий скалярний тип визначає допустимість всіх операцій і відношень над значеннями обмеженого типу. Обмежені типи дають можливість описувати алгоритм у більш наочній формі. Крім цього, у процесі трансляції і виконання програми з’являється можливість економити пам’ять і здійснювати контроль присвоювань.
Приклад 7.5.
Program Time_Table;
Type
Weekday = (Monday, Tuesday, Wednesday, Thursday, Friday,
Saturday, Sunday);
Workday = Monday .. Friday;
Var
i : Workday;
Begin
For i := Monday to Friday do
Case i of
Monday: Writeln(‘фізика‘, ’інформатика‘, ’історія’);
Tuesday, Friday: Writeln(‘мат. аналіз‘,’історія‘, ‘англійська’);
Wednesday, Thursday: Writeln(‘фізика ‘,’алгебра‘,’інформатика’)
end
End.
7.4. Складні (складені) типи
У мові Pascal реалізований механізм визначення складних (складених) типів даних. Новий тип даних визначається як структурована сукупність даних-компонент стандартних або раніше визначених типів. Оскільки типи компонент можуть бути також складеними, можна будувати складні ієрархії типів. Методи структурування даних у мові дозволяють будувати масиви, записи, множини і файли. Ці методи називають статичними, оскільки їх опис здійснюється попередньо. Більш складні структури можна створити динамічно – у процесі виконання програми – за допомогою посилань. При вивченні складних типів основна увага приділяється способам конструювання даного і способам доступу до компонентів даного.
7.5. Регулярний тип. Масиви
Значеннями регулярного типу є масиви. Масив – це найбільш поширена структура даних. У багатьох мовах програмування, що були одними з перших мов високого рівня, (Fortran, Algol-60, Basic) це єдиний явно визначений складний тип.
Масив – це послідовність однотипних даних, що об’єднана спільним іменем, елементи (компоненти) якої відрізняються індексами.
Індекс елемента вказує місце (номер) елемента в масиві. Кількість елементів масиву фіксована і визначена в його описі. Доступ до елемента масиву здійснюється обчисленням значення його індексу. Тому масиви – це структури даних з прямим (випадковим) доступом. Всі компоненти масиву є однаково доступними. При визначенні регулярного типу задається і тип компонент, і тип індексів. Саме визначення має вид:
<ім’я типу > = Array [< тип індексу >] of <тип компоненти >;
Масив
Приклади:
а) Type
LinearTable = Array [0..100] of Integer;
б) Type
Letter = ‘a’..’z’;
Word = Array [1..20] of Letter;
Order = Array [Letter] of Integer;
в) Type
Matrix = array [1..N] of array [1..M] of Real;
г) Type
Tenzor = array [-10..10] of array [0..20] of array [0..3] of Real;
У прикладі в) М і N – константи цілого типу. Зверніть увагу на те, що значення типу Matrix - M*N матриці – визначаються як масиви, компонентами яких, в свою чергу, є масиви з дійсних чисел.
Регулярний тип, значеннями якого є багатомірні масиви (наприклад, в) і г)), можна визначати в скороченому виді:
Type <ім’я> = Array [<Tип> {,<Tип>} ] of <тип компоненти>;
Наприклад:
а) Type
Matrica = array [1..N,1..M] of real;
б) Type
Index1 = -10..10;
Index2 = 0..20;
Index3 = 0..3;
Tenzor = Array [Index1, Index2, Index3] of Real;
в) Type
Labyrinth = array [1..100,1..100] of Boolean;
Типи Real і Integer не можуть бути типами індексів!
Компонента змінної - масиву явно позначається іменем змінної, за яким у квадратних дужках слідують індекси; індекси є виразами типу індексу. Наприклад, Table[1, i+j ], T[2*i+1, (j*j) mod i], S[Monday, Friday]. Зверніть увагу на те, що на відміну від індексних виразів, межі індексів у змінних - масивах повинні бути константами. Значення індексних виразів повинні бути значеннями типу індексу, тобто знаходитись в межах, що визначені межами індексів.
Розглянемо приклади:
Приклад 7.6. Програма обчислює скалярний добуток вектора V і вектора V`, отриманого з V перестановкою координат у зворотному порядку.
Program ScalarMult;
Const
n = 10;
Type
Vector = array[1..n] of Real;
Var
V : Vector;
Procedure InpMas(Var V : Vector);
Var i : Integer;
Begin
For i := 1 to n do begin { блок читання вихідного вектора }
Write(‘Введіть координату вектора : ‘);
Readln(V[i]);
end;
End;
Function Sum (Var V: Vector): Real;
Var i : Integer;
Summa : Real;
Begin
Summa := 0; { блок обчислень}
For i := 1 to n do
Summa := Summa + V[i]*V[n-i+1];
Sum:= Summa;
End;
Begin
InpMas(V );
write(‘ Результат : ‘,Sum (V));
End.
Блок обчислень можна оптимізувати за часом. Зазначимо, що Summa обчислюється за формулою: : Summa = V[1]*V[n] + V[2]*V[n-1] +...+ V[2]*V[n-1] + V[1]*V[n]. Отже, її доданки, рівновіддалені від кінців, рівні. Тому кількість повторень циклу можна зменшити вдвоє. При цьому необхідно враховувати парність числа n:
{ Program ScalarMult1;}
For i := 1 to n div 2 do
Summa := Summa + V[i]*V[n-i+1];
If Odd(n)
then Summa := 2*Summa
else Summa := 2*(Summa + V[n div 2 + 1];
7.6. Пошук елемента в масиві
Задача пошуку елемента в послідовності – одна з важливих задач програмування як з теоретичної, так і практичної точок зору. Ось її формулювання:
Нехай A = {a1, a2, ...} – послідовність однотипних елементів і b – деякий елемент, який має властивість P. Знайти місце елемента b в послідовності А. Оскільки представлення послідовності в пам’яті може бути здійснено в виді масиву, задачі можуть бути уточнені як задачі пошуку елемента в масиві A:
o Знайти максимальний елемент масиву;
o Знайти даний елемент масиву;
o Знайти k-тий за величиною елемент масиву;
Найбільш прості і часто оптимальні алгоритми основані на послідовному перегляді масиву A з перевіркою властивості P на кожному елементі.
Приклад 7.7. Пошук мінімального елемента в масиві.
Const
n = 10;
Type
Vector = array[1..n] of Real;
Рrocedure MinItem (Var A: Vector; Var Min: Real);
Var
i : Integer;
Begin
Min := A[1];
For i := 1 to n do begin
If Min > A[i]
then Min := A[i]
end;
End;
Begin
{Блок введення масиву}
MinItem (A, Min);
{Виведення значення Min}
End.
Ми пропонуємо читачу розглянути поведінку цього алгоритму і його модифікації у випадку, коли мінімальних елементів у масиві декілька і треба знайти перший, останній, а також всі мінімальні елементи.
7.7. Ефективність алгоритму за часом
Раніш, ніж розглянути задачу пошуку даного елемента, відзначимо важливу відмінну особливість алгоритмів обробки масивів: їх складність визначається характерними параметрами – розмірами вхідних масивів. У розглянутих вище прикладах розмір входу – константа n.
Програма Складність Оцінка складності
ScalarMult T(n) = Tb*n T(n) = O(n)
ScalarMult1 T(n) = Tb*n/2 T(n) = O(n)
MinElement T(n) = Tb*n T(n) = O(n)
Тут T (b) - складність тіла (внутрішнього) циклу. В реальних програмах величина Tb залежить від багатьох факторів, зв’язаних з апаратурою, операційною системою і системою програмування. Тому якість алгоритму, реалізованого у виді програми і не залежного від зовнішніх обставин можна оцінити функцією параметра задачі. При цьому основна властивість функції оцінки складності – швидкість її росту. Для алгоритму ScalarMult ця функція зростає лінійно. Цей факт відображений формулою T(n) = O(n).
Абстрагування від деталей реалізації програми дає можливість оцінювати алгоритми розв’язування задач і їх реалізацію у виді програми. Мірою ефективності алгоритму є оцінка його складності.
Розглянемо задачу пошуку даного елемента в масиві. Очевидний алгоритм її розв’язання, як і в попередній задачі – послідовний перегляд масиву і порівняння кожного елемента масиву з даним. Відміна полягає в тому, що коли елемент знайдений, перегляд можна припинити. Це означає, що виконання циклу переривається. У мові є засіб переривання – оператор переходу.
7.8. Мітки. Оператор переходу. Застосування оператора переходу для дострокового виходу з циклу
Оператор переходу вказує, що подальша робота (виконання програми) повинна продовжуватись з іншої точки програми, а саме, з оператора, відміченого міткою.
Оператор має вид:
Goto < мітка >
Мітка представляє собою ціле число без знака, що складається не більш ніж з 4 цифр. У розділі операторів кожна мітка може зустрічатися тільки перед одним оператором. Кожна мітка, що зустрічається в розділі операторів, повинна бути описана в розділі міток.
Розділ міток визначений наступною діаграмою:


 Обмежений
Обмежений