Задача 21. Оптимальне сортування 4-х елементів. Скласти алгоритм упорядкування 4-х елементів, що виконував би всього 5 порівнянь, тобто С(4) = 5.
Вказівка: Упорядкувати пари (а1, а2) і (а3, а4) а потім, побудувавши дерево розв’язувань, знайти порівняння і перестановки, що вирішують задачу.
Задача 22. Два числових інтервали [a, b] і [c, d] задані числами a, b, c, d. Скласти алгоритм пошуку їх перетину.
Задача 23. Два числових інтервали [a, b] і [c, d] задані числами a, b, c, d. Скласти алгоритм, що визначає, чи є об'єднання цих інтервалів також інтервалом.
Задача 24. Скласти оптимальний алгоритм, що переставляє дані a, b, c, d таким чином, щоб найменше з них стояло на першому місці, а найбільше – на 4-ому.(Тобто a = Min(a, b, c, d), d = Max(a, b, c, d)). Визначити кількість порівнянь і перестановок алгоритму.
Задача 25*. Оптимальне сортування 5-ти елементів. Скласти алгоритм упорядкування 5-ти елементів, що виконував би всього 7 порівнянь ( С(5) = 7 ).
6.7. Оптимізація розгалужень
Складність програми, що розгалужується, визначається складністю умови і складністю обчислень гілок. На відміну від програми, що не розгалужується, час виконання тут залежить від гілки, якою слідує процес виконання. Тому для таких програм має смисл поняття складності програми в гіршому випадку і складності програми в середньому.
Хай Тп - складність програми за часом в гіршому випадку, Ту - складність за часом умови і Тв1, Тв2 - складності гілок за часом програми. Тоді має місце співвідношення:
Tп = Tу + Max( Tв1, Tв2 ) (1)
Складність за часом у середньому визначається формулою
Tп = Tу + PуTв1 + (1 - Pу)Tв2 (2)
де Ру - ймовірність виконання умови.
Оскільки умовою є логічний вираз, загальні прийоми оптимізації виразів застосовуються і для логічних виразів. Час Tл виконання логічних операцій And, Or, Not, =, <> значно менше часу виконання адитивних операцій, а час виконання операцій <, >, <=, >= дорівнює часу виконання аддитивних операцій.
Tf >> Tm > Ta > Tл (3)
Розглянемо приклад: потрібно з’ясувати, чи дорівнює нулю одне з двох чисел А, В .
1 варіант умови: А * В = 0
2 варіант умови: (А = 0) Оr (В = 0)
У першому варіанті використані множення і порівняння, у другому - 3 логічних операції. Складність 2-го варіанта менша.
У програмах з багатозначним розгалуженням, коли в управлінні використовується декілька умов або обчислень логічних виразів, існує можливість оптимізації управління обчисленнями. Наприклад, наступні обчислення еквівалентні:
If x < 0 then <==> If (x < 0) And (Y < 0)
If y < 0 then z := 1 then z := 1
If x < 0
then Flag := False <==> Flag := (x >= 0)
else Flag := True
У наступному прикладі умови розгалужень спрощені за рахунок використання співвідношень, що виконуються після обчислення попередньої умови:
Приклад 6.2. Програма обчислення значення кусково-визначеної функції:
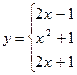
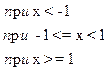
1 варіант ( який часто зустрічається у починаючих)
If x < -1 then y := 2*x - 1;
If (-1 <= x) And (x < 1) then y := Sqr(x) + 1;
If x >= 1 then y := 2*x + 1;
2 варіант ( оптимальний )
If x < -1
then y := 2*x - 1
else If x < 1
then y := Sqr(x) + 1
else y := 2*x + 1;
Дійсно, умови x < -1, (-1 <= x)And(x < 1), x >= 1 взаємно протилежні і у сукупності тотожно істинні. Тому (-1 <= x) і x >= 1 можна замінити на else.
6.8. Розділ типів. Перелічуваний тип
Поряд зі стандартними типами даних у мові Pascal широко використовуються типи, що визначаються програмістом. Один з таких типів – це перелічувальний тип. Визначення цього типу задає упорядковану множину значень шляхом перелічення імен, що позначають ці значення.
Типи даних, що визначає програміст, описуються у спеціальному розділі – розділі типів. Розділ типів визначений синтаксичною діаграмою:
Розділ
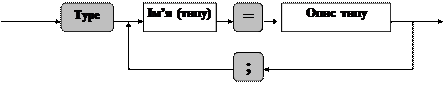 типів
типів
Перелічувальний тип даних визначається наступною діаграмою:



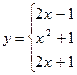
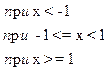
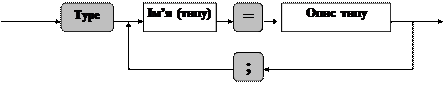 типів
типів