Побудови в графічному редакторі і на аркуші паперу дещо відрізняються, тому що комп’ютерні інструменти не зовсім ідентичні звичним. Наприклад, графічний редактор не має лінійки, в ньому немає інструменту, подібного до транспортиру, в колі, намальованому в графічному редакторі, не визначений центр. Тому необхідно навчитися будувати моделі геометричних операцій: ділення відрізка і кута на рівні частини, визначення центра кола та ін. Це можна зробити, використовуючи закони геометрії.
Приклад.1 Моделювання ділення відрізка навпіл.
Формалізація:
Об’єктом моделювання є відрізок деякої довжини a.
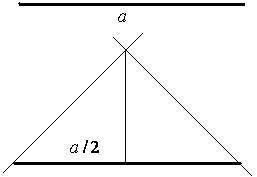
Побудова заснована на тому, що висота рівнобедреного трикутника є одночасно бісектрисою і медіаною. Для побудови вистачить інструменту «лінія» і клавіші Shift.
Алгоритм ділення:
– малюємо відрізок деякої довжини a. Цей відрізок ми маємо поділити навпіл;
– малюємо ще один відрізок (за довжиною цей відрізок має бути майже такий самий як перший). За допомогою пункту меню графічного редактора растянуть/наклонить нахиляємо цей відрізок на 450, після чого копіюємо, вставляємо та за допомогою команди отразить/повернуть відображаємо зліва направо;
– із отриманих елементів складаємо трикутник із основою a. Опускаємо висоту на основу. Ця висота і ділить відрізок a навпіл.
Приклад.2 Побудова рівностороннього трикутника із заданою стороною.
Формалізація:
Об’єктом моделювання є трикутник, що складається з трьох відрізків однакової довжини.
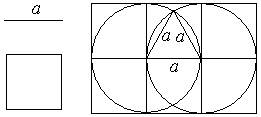Для побудови використовується квадрат, довжина сторони якого дорівнює довжині сторони трикутника, і вписане коло, яке має таке саме значення радіусу. Подібний алгоритм використовується на уроках геометрії при побудові рівностороннього трикутника за заданою стороною за допомогою циркуля.
Алгоритм побудови:
– малюємо відрізок деякої довжини а;
– за допомогою копіювання та пункту меню графічного редактора отразить/повернуть складаємо квадрат із стороною a. Далі за допомогою копіювання складаємо квадрат із стороною 2a та вписуємо в нього коло. Радіус цього кола буде дорівнювати половині довжини квадрата, у який воно вписане, тобто a;
– отриманий малюнок знову копіюємо;
– два отримані кола розташовуємо таким чином аби вони перетинали центри одне одного. Поєднуємо прямими лініями центри кіл із точкою їх перетину.
Так як радіуси кіл однакові і вони дорівнюють a, то ми отримали трикутник із заданою стороною.
Завдання для самостійного виконання.
1) Ділення відрізка на n рівних відрізків.
Побудова заснована на теоремі Фалеса: якщо на одній прямій відкласти декілька рівних відрізків і через їх кінці провести паралельні прямі, що перетинатимуть другу пряму, то вони відтинатимуть на другій прямій відрізки рівні між собою. Паралельність ліній досягається копіюванням.
2) Побудова кола заданого радіусу і визначення його центру.
При побудові використовувати ту властивість, що діаметр кола дорівнює довжині сторони квадрата, описаного навколо цього кола.
3) Ділення кута навпіл.
В якості додаткових побудов використовується коло будь-якого радіусу. В його центр поміщують копію кута, який треба поділити.
4) Побудова правильного шестикутника із заданою стороною.
Можна використати властивість правильних фігур вписуватися в коло і те, що сторона рівностороннього шестикутника дорівнює радіусу описаного кола.
5) Побудувати рівнобедрений трикутник за заданою основою і висотою.
Використати те, що у рівнобедреного трикутника висота, що проведена із кута між рівними сторонами на основу, є і бісектрисою і медіаною.
6) Побудувати прямокутний трикутник за гіпотенузою і катетом.
Використати ту властивість, що якщо у трикутника, вписаного в коло, однією із сторін є діаметр цього кола, то трикутник прямокутний. В якості допоміжних побудов використовуються два кола, діаметр одного з них має дорівнювати гіпотенузі, а радіус іншого – довжині катета.
7) Побудувати рівнобедрений трикутник за боковою стороною і кутом при вершині.
Це можна зробити, використовуючи команди графічного редактора «растянуть/наклонить» (кут нахилу дорівнює половині даного) і «отразить/повернуть».
8) Побудувати трикутник за трьома сторонами.
Врахувати, що сума будь-яких двох сторін трикутника, має бути більшою за довжину третьої сторони, а різниця довжин двох сторін – меншою за довжину третьої сторони. В якості допоміжних побудов використовуються два кола, радіуси яких дорівнюватимуть довжинам бокових сторін.
9) Побудувати правильний восьмикутник із заданою стороною.
Можна використати властивості правильних фігур вписуватися в коло. В якості допоміжних побудов взяти коло, яке вписане в квадрат із двома проведеними діагоналями.
10) Побудувати трикутник за двома сторонами і кутом між ними.
Це можна зробити, використовуючи команду графічного редактора «растянуть/наклонить» (кут нахилу дорівнює половині даного).
11) Побудувати паралелограм за заданими сторонами і гострим кутом.
Для отримання необхідного кута використовувати команду графічного редактору «растянуть/наклонить».
12) Побудувати трапецію за чотирма сторонами.
Для цієї побудови скористатися двома колами, радіуси яких дорівнюють довжинам бокових сторін трапеції, та паралельністю основ трапеції.
