Одним із фундаментальних понять програмування (детальніше про більшість з них ми будемо вести розмову пізніше) є тип даних, який визначає, по-перше, множину значень, по-друге, множину допустимих операцій із цими значеннями і нарешті, спосіб збереження значень та виконання операцій. Тобто, будь-яка інформація, якою оперує програма, відноситься до певного типу даних. В чому полягає необхідність такого підходу?
Справа в тому, що навіть у мовах низького рівня, зокрема в мові Асемблер, для дійсних та цілих чисел відводяться різні об’єми пам’яті, а отже, і дії з ними виконуються по-різному. В мовах високого рівня цей факт також не міг не знайти свого відображення. Крім того, типи даних в програмуванні просто не можуть однозначно відповідати прийнятим у математиці типам чисел. Так, у математиці множина цілих чисел не обмежена ні знизу, ні згори. Реалізувати подібний тип у комп’ютері неможливо. Тому, як правило, у мовах програмування для різних видів обчислень використовується множина типів цілих чисел, які мають різні діапазони значень в залежності від виділеного для них об’єму пам’яті.
Для довідки, мінімальна одиниця інформації в комп’ютері складає 1 біт (1б), в якому якраз і може бути записані 0 або 1. 1 байт (1Б) об’єднує вісімку бітів, а далі все одноманітно – 1 КБ(кілобайт) = 1024 Б (1024 = 210), 1 МБ(мегабайт) = 1024 КБ, 1 ГБ(гігабайт) = 1024 МБ.
Розглянемо (коротко) кодування інформації за допомогою двійкової системи числення. Будь-яка позиційна система числення з основою (базою) q системи числення вимагає відповідно q символів для представлення будь-якого числа. Так, в десятковій системі числення використовується 10 цифр від 0 до 9, в двійковій всього 2 цифри – 0 та 1, в 16-ковій – 16 символів – це цифри від 0 до 9 та 6 латинських літер від A до F. Їх відповідність між собою показано у наступній таблиці.
| 10-кова система
| 2-кова система
| 16-кова система
| 10-кова система
| 2-кова система
| 16-кова система
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A
|
|
|
|
|
|
| B
|
|
|
|
|
|
| C
|
|
|
|
|
|
| D
|
|
|
|
|
|
| E
|
|
|
|
|
|
| F
|
Нехай тепер 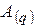 – довільне дійсне число, записане у позиційній системі числення з основою
– довільне дійсне число, записане у позиційній системі числення з основою 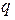 . Тоді, якщо його запис в цій системі має вигляд
. Тоді, якщо його запис в цій системі має вигляд 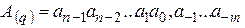 , то
, то
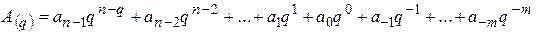 . (1)
. (1)
Наприклад, 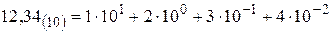 , або
, або
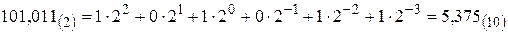 .
.
Формулу (1) можна записати у вигляді:
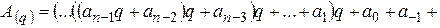
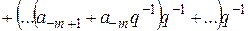 .
.
Тепер зрозуміло, що для переведення цього числа з десяткової системи числення у систему числення з основою 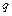 , для визначення цілої частини числа треба ділити його цілу частину на основу
, для визначення цілої частини числа треба ділити його цілу частину на основу 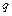 ,записуючи залишки у зворотному порядку, до тих пір, поки не одержимо результат, рівний 0 або 1. А для визначення дробової частини – треба взяти дробову частину у десятковій формі та множити її на основу
,записуючи залишки у зворотному порядку, до тих пір, поки не одержимо результат, рівний 0 або 1. А для визначення дробової частини – треба взяти дробову частину у десятковій формі та множити її на основу 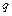 , записуючи кожного разу цифри, які отримуватимемо у цілій частині результату. Множення виконувати до тих пір, поки дробова частина результату не стане нульовою, або не заповнимо розрядну сітку.
, записуючи кожного разу цифри, які отримуватимемо у цілій частині результату. Множення виконувати до тих пір, поки дробова частина результату не стане нульовою, або не заповнимо розрядну сітку.
Розберемо приклад. Нехай маємо перевести число 123(10) до двійкової та шістнадцяткової систем числення. При діленні числа 123 на 2 одержимо 61 і залишок 1. Залишок запам’ятаємо, а результат 61 ділимо на 2 знову. Одержуємо 30 і залишок 1. Продовжуючи процес, одержимо залишки (перевірте!) 0, 1, 1. Врешті решт отримаємо залишок 1 і результат 1. Запишемо ці цифри у зворотному порядку: 1111011(2)= 123(10) .Для одержання 16-кового представлення розділимо число у двійковій формі на четвірки цифр і знайдемо відповідні 16-кові цифри у таблиці: 1111011(2)= 01111011(2)=7B(16).
Нехай тепер маємо дробове число 0,4567(10),яке переведемо у 2-ковий дріб. При цьому вважатимемо, що розрядна сітка рівна 8 символам. Отже, множимо 0,4567 на 2 і фіксуємо значення цілої частини результату. Маємо 0,9134, запам’ятаємо 0. Знову множимо лише дробову частину результату, матимемо 1,8268. Запам’ятаємо 1 і множимо 0,8268. Продовжуємо, поки не отримаємо 8 цифр. Таким чином одержимо (перевірте!) 0,4567(10) ≈ 0,01110100(2) ≈ 0,74(16).


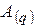 – довільне дійсне число, записане у позиційній системі числення з основою
– довільне дійсне число, записане у позиційній системі числення з основою 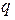 . Тоді, якщо його запис в цій системі має вигляд
. Тоді, якщо його запис в цій системі має вигляд 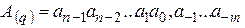 , то
, то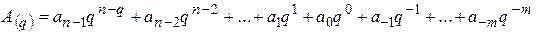 . (1)
. (1)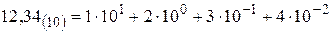 , або
, або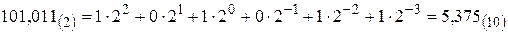 .
.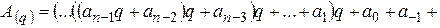
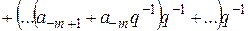 .
.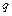 , для визначення цілої частини числа треба ділити його цілу частину на основу
, для визначення цілої частини числа треба ділити його цілу частину на основу