Матриця Карно для трьох вхідних змінних (значення функції довільні).
Карта (матриця) Карно дозволяє записати логічний вираз у мінімізованому вигляд за рахунок об’єднання клітинок матриці за певними правилами, наведеними нижче.
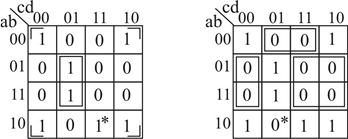
При запису значень наборів змінних сусідні стовпці (строки) відрізняються значенням тільки однієї змінної. При оптимізації логічної функції записуються тільки ті змінні, які не міняють свого значення всередині вибраного об’єднання. Розглянемо оптимізація ЛФ на наступному прикладі:
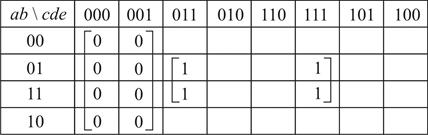
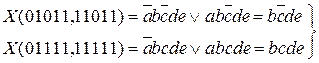 далі,
далі, 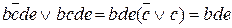
У результаті, Х для «1» буде містити тільки змінні 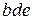 .
.
Правила для об’єднань значень функції:
1. Всі одиниці (для ДНФ) або нулі (для КНФ) повинні бути об’єднані у прямокутні контури. Об’єднання одиниць (нулів) не повинно мати всередині себе нулів (одиниць).
2. Однойменні контури можуть накладатись один на один або мати розрив. Не допускаються лишні контури.
3. Контур повинен об’єднувати 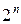 клітин. Площа контуру повинна бути симетричною відносно власного центру.
клітин. Площа контуру повинна бути симетричною відносно власного центру.
4. Контури об’єднують тільки симетричні клітини.
5. Кожній одиничній (нульовій) клітині відповідає кон’юнкція (диз’юнкція) вхідних змінних, які визначають дану клітину.
6. Найбільш оптимальний логічний вираз виходить при утворенні найбільших контурів. При оптимізації у логічний вираз записуються тільки ті змінні, котрі не змінюють свого значення всередині обраного контуру. Якщо яка-небудь одиниця (нуль) не може бути об’єднана у контур, то для неї записується кон’юнкція (диз’юнкція) всіх змінних, які визначають дану клітину.
Логічні функції, значення яких одностайно визначено на всіх наборах змінних, називаються повністю заданими.
Логічні функції, значення яких визначено не на всіх наборах, називаються не повністю заданими. А такі набори є невизначеними.
Приклад не повністю заданої функції.
Невизначені умови у матриці можна об’єднати як з нулями, так і з одиницями, виходячи з того, наскільки це зручно при оптимізації задачі.




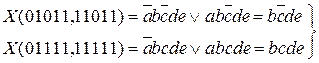 далі,
далі, 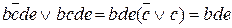
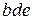 .
.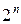 клітин. Площа контуру повинна бути симетричною відносно власного центру.
клітин. Площа контуру повинна бути симетричною відносно власного центру.