Першим етапом математичного моделювання є постановка завдання, визначення об'єкту і цілей дослідження, задання критеріїв (ознак) вивчення об'єктів і управління ними. Неправильна або неповна постановка завдання може звести нанівець результати всіх подальших етапів.
Раніше наголошувалося, що планування експерименту базується на кібернетичних уявленнях про об'єкт досліджень. У зв'язку з цим, при новому підході до проведення експериментальної праці найбільш відповідною моделлю об'єкту досліджень рекомендується вибирати так званий «чорний ящик» (рис. 1).
Рисунок 1 – Модель об’єкта досліджень на стадії постановки задачі
Принципи побудови такої моделі зазвичай відповідають апріорним уявленням експериментатора про об'єкт досліджень при вирішенні, в умовах неповного знання механізму, явищ складних багатофакторних завдань.
Входи, позначені стрілками, направленими до об'єкту, характеризують всі способи можливої дії на об'єкт досліджень (це вхідні параметри).
Виходи, які позначені стрілками, направленими від об'єкту, характеризують якість об'єкту досліджень (це вихідні параметри або критерії оптимізації). Поняття «Критерій оптимізації» інколи замінюють поняттям «цільова функція».
До вхідних параметрів відносять керуючі, контрольовані і обурюючі параметри.
Керуючі параметри (або чинники) 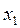 ,
, 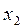 , ...,
, ..., 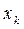 є основними. На них можна впливати з метою зміни значень критеріїв оптимізації (управління станом об'єкту оптимізації).
є основними. На них можна впливати з метою зміни значень критеріїв оптимізації (управління станом об'єкту оптимізації).
Контрольовані параметри ( 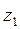 ,
, 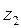 , ...,
, ..., 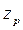 ) вимірюють в процесі дослідження, їх не змінюють цілеспрямовано (зазвичай можливість дії на них відсутня).
) вимірюють в процесі дослідження, їх не змінюють цілеспрямовано (зазвичай можливість дії на них відсутня).
Обурюючі параметри ( 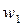 ,
, 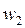 , ...,
, ..., 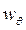 ) - неконтрольовані, вони недоступні для виміру, їх значення змінюються в часі випадковим чином.
) - неконтрольовані, вони недоступні для виміру, їх значення змінюються в часі випадковим чином.
Чинники можуть набувати певних значень, які називають рівнями варіювання чинників. Кожному стану чорного ящика відповідає певне поєднання рівнів всіх чинників. Чим більше сукупність всіх можливих різних станів чорного ящика, тим він складніший і тим важче вирішувати завдання, пов'язані з його вивченням як об'єкту досліджень.
Формалізація апріорної інформації, заснована на аналізі літературних даних, опитуванні фахівців про доцільність проведення науково-дослідної роботи, дозволяє правильно вибрати критерії оптимізації і чинники, а також визначити положення нульової точки - точки і області експерименту, з якої бажано починати експеримент. На цій же стадії роботи вирішується питання про прийняття обмежень на фактори. Якщо завдання має бути зв'язане з врахуванням двох і більше критеріїв оптимізації, то одночасно розглядаються необхідні обмеження для функції мети, оскільки в цьому випадку при пошуку оптимального рішення без обмежень рекомендується рухатися до оптимуму лише по одному критерію (при певних обмеженнях на інші).
Основные задачи математической статистики. Выборки и их характеристики.
§ 1. Предмет и задачи математической статистики.
Математическая статистика- раздел математики, тесно связанный с теорией вероятности. МС занимается изучением закономерностей, которым подчиняются массовые явления, на основе результатов наблюдений. Различие между теорией вероятности и математической статистикой:
· Типичные задачи теории вероятности - по известным вероятностям простых случайных событий вычислить вероятность более сложных событий;
· Типичные задачи математической статистики - на основании результатов наблюдений оценить вероятность случайного события или вероятность характеристики случайной величины.
При решении любой задачи математической статистики имеется 2 источника информации:
1. результаты наблюдений, экспериментов;
2. априорная (доопытная) информация о свойствах изучаемого объекта, накопленная к текущему моменту.
Перечислим некоторые задачи математической статистики:
· Предварительная обработка данных - упорядочение результатов наблюдения или эксперимента, представление их в обозримом виде;
· Оценка неизвестной величины (вероятности события, функции распределения случайной величины, параметров распределения, степени взаимозависимости двух или нескольких случайных величин);
· Проверка статистических гипотез (о виде функций распределения, о вероятности событий и т.п ), т.е установление меры надежности оценок, сделанных на основании опытных данных;
· Установление формы и степени связи между случайными величинами.
Современная математическая статистика может быть определена как теория принятия решений в условиях неопределенности.
§ 2. Генеральная и выборочная совокупность. Способы отбора.
Если нужно изучить, как в совокупности однородных объектов распределен некоторый признак, характеризующий эти объекты, не всегда возможно исследовать каждый объект. В этих случаях отбирается часть объектов и по свойствам отобранных объектов судят о свойствах всех объектов.
Выборкой или выборочной совокупностью называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют исходное множество объектов, из которых производится выборка.
Объем совокупности (выборочной или генеральной) – это число элементов данного множества.
При осуществлении отбора возможны два способа:
· Выборка называется повторной,если случайно отобранный для обследование объект возвращается в генеральную совокупность перед отбором следующего объекта. В противном случае выборка называется бесповторной.
Чтобы по данным выборки можно было судить о всей совокупности, необходимо чтобы члены выборки представляли её достаточно правильно. Такая выборка называется репрезентативной (представительной).
Для того чтобы выборка была репрезентативной необходимо:
1. Случайный отбор элементов совокупности;
2. Равновероятность попадания в выборку любого элемента генеральной совокупности;
3. Достаточно большой объем выборки.
Для обеспечения случайности отбора и равновероятности попадания в выборку применяются различные методы отбора:
· Если элементы извлекаются по одному из генеральной совокупности, говорят о простом случайном отборе.(повторный, бесповторный);
· Если из генеральной совокупности элементы разбиваются на группы (серии), серия отбирается случайно и подвергаются сплошной проверке, то отбор называется серийным;
· Типический отбор осуществляется следующим образом:
-генеральная совокупность делится на типические части и из каждой части производится случайный отбор;
· Механический отбор осуществляется через регулярный интервал (например, проверяется каждая 20 деталь).
§ 3. Статистическое распределение выборки.
Пусть из генеральной совокупности извлечена выборка и производятся наблюдения за случайной величиной  (признак), причем значение
(признак), причем значение 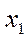 наблюдалось
наблюдалось 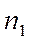 -раз, значение
-раз, значение 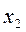 наблюдалось
наблюдалось 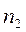 -раза,
-раза, 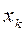 –
–  -раз и т.д.
-раз и т.д.
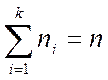
Возможные значения случайной величины  ,
, 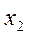 ,
, 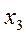 ,….
,…. 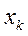 ,принято называть вариантами, а последовательность вариант, записанную в порядке возрастания - вариационным рядом.
,принято называть вариантами, а последовательность вариант, записанную в порядке возрастания - вариационным рядом.
Числа  ,
, 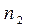 ,…
,…  называют частотами.
называют частотами.
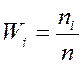 где
где 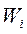 - относительная частота.
- относительная частота.
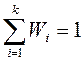
Перечень вариант и соответствующих им частот (или относительных частот) называется статистическим распределением выборки (или статистическим рядом). Обычно статистический ряд записывают в виде таблицы.
§ 4. Полигон и гистограмма.
Для наглядности часто используют графическое изображение статистических рядов:
1. для дискретного ряда – полигон;
2. для интервального ряда – гистограмма.
Полигон частот (относительных частот), есть ломанная, отрезки которой соединяют точки ( 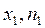 ), (
), ( 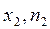 ),…..(
),…..(  ) или (
) или (  ),(
),(  )….(
)….(  ).
).
Гистограмма частот ( 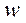 ) есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной
) есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной 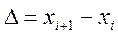 и высотами
и высотами 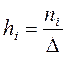 или
или 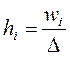 .
.
Площадь всей гистограммы частот равна n (объем выборки).
Площадь всей гистограммы относительных частот равна 1.
§ 5 Эмпирическая функция распределения.
Пусть задано статистическое распределение случайной величины  .
.
Обозначим через 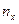 - число вариант,меньших
- число вариант,меньших  .
.
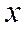 - любое действительное число.
- любое действительное число.
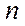 - объем выборки.
- объем выборки.
Относительная частота событий {Х<x}= 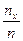 .
.
При изменении  меняется и относительная частота, т.е отношение
меняется и относительная частота, т.е отношение 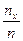 является функцией от х.
является функцией от х.
Поскольку данная функция строится по данным опыта, то она называется эмпирической.
Эмпирической функцией распределения (функцией распределения выборки F*(x)) называется относительная частота события  , где
, где 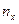 - число вариант меньших x, n- объем выборки.
- число вариант меньших x, n- объем выборки.
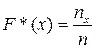
Теоретической функцией распределения называется функция распределения F( 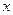 ) случайной величины
) случайной величины  , вычисленная по генеральной совокупности, т.е вероятность события
, вычисленная по генеральной совокупности, т.е вероятность события 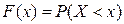 .
.
Теорема.
При неограниченном возрастании объема выборки эмпирическая функция распределения сходится по вероятности к теоретической функции распределения.
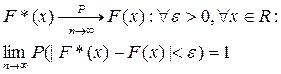
§ 6. Числовые характеристики статистического распределения выборки.
Пусть имеется генеральная совокупность выборки объема N ,из которой сделана выборка объема n.
Статистический ряд, в котором присутствуют значения случайной величины X и относительные частоты их появления, можно рассматривать как закон распределения новой случайной величины  , а исходную случайную величину –
, а исходную случайную величину – 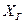 .
.
Очевидно, что законы распределения этих величин в какой-то мере близки, но не совпадают. Каждой числовой характеристике случайной величины 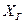 соответствует её выборочный аналог- характеристика случайной величины
соответствует её выборочный аналог- характеристика случайной величины  .
.
При возрастании объема выборки ( 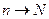 ), числовые характеристики случайной величины
), числовые характеристики случайной величины  (СВХ) будут сходиться по вероятности к соответствующим характеристикам
(СВХ) будут сходиться по вероятности к соответствующим характеристикам 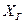 .
.
Наиболее употребительны следующие числовые характеристики выборки:
1. Выборочное среднее ( 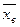 )-среднее арифметическое значений выборки:
)-среднее арифметическое значений выборки:
 ;
;
2. Выборочная мода ( 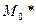 )- наиболее вероятное значение в выборке (варианта с наибольшей частотой);
)- наиболее вероятное значение в выборке (варианта с наибольшей частотой);
3. Выборочная медиана ( 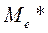 ) - значение случайной величины, приходящейся на середину вариационного ряда;
) - значение случайной величины, приходящейся на середину вариационного ряда;
а) если объем выборки четный, то 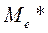
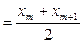 ;
; 
 ;
;
б) если объем выборки нечетный, то 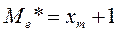 ;
; 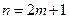 ;
;
В теории вероятности медиана определяется: 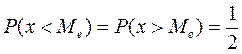 .
.
4. Выборочная дисперсия - средние значение квадрата отклонения 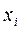 от
от
выборочной средней 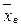
 ;
;
5. Выборочное среднее квадратичное отклонение:
 ;
;
6. Исправленная выборочная дисперсия:
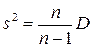 ;
;
7. Исправленное среднее квадратичное отклонение:
 ;
;
Для интервального статистического ряда все вышеприведенные формулы сохраняются, но в качестве значений вариант берутся середины соответствующих промежутков [ 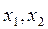 ), [
), [ 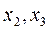 ), …..[
), …..[ 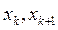 ) т.е
) т.е
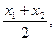
 …..
….. 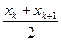 .
.

§ 7. Числовые характеристики генеральной совокупности.
Для генеральной совокупности объема N с распределенным количественным признаком  также можно ввести числовые характеристики:
также можно ввести числовые характеристики:
1. генеральная средняя - это среднее арифметическое значений признака 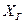
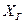 =
= 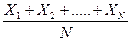 .
.
Если в генеральной совокупности значения признака имеют частоты 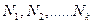 , причем (
, причем ( 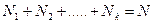 ), то
), то
 .
.
2. генеральная дисперсия - это среднее по генеральной совокупности значение квадрата отклонения 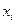 от генерального среднего
от генерального среднего 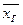 ,
,
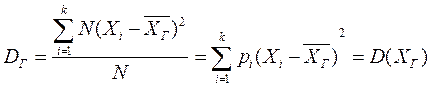
3. Генеральное среднее квадратичное отклонение (стандартное отклонение)
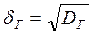
По мере увеличения объема выборки ( 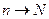 ) числовые характеристики случайной величины
) числовые характеристики случайной величины  будут приближаться к соответствующим характеристикам
будут приближаться к соответствующим характеристикам 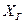 , т. е
, т. е
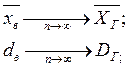
Следовательно, и при произвольном объеме выборки значения выборочных характеристик в какой-то мере служат оценками генеральных характеристик.
Статистические оценки параметров распределения.
§1 Понятие о статистических оценках параметров распределения.
Пусть имеется генеральная совокупность объема N, исследуется случайная величина 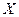 , сделана выборка объема n и получены значения
, сделана выборка объема n и получены значения 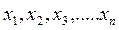 .
.
Выборка- это последовательность одинаково распределенных независимых случайных величин 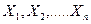 , распределение которых совпадает с распределением случайной величины
, распределение которых совпадает с распределением случайной величины 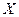 в генеральной совокупности.
в генеральной совокупности.
Конкретный набор чисел, 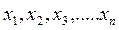 полученный при выборке n объектов из генеральной совокупности, называется реализацией выборки.
полученный при выборке n объектов из генеральной совокупности, называется реализацией выборки.
Таким образом, введенные ранее числовые характеристики выборочного распределения оказываются зависящими от конкретной реализации выборки, т.е. – это случайными величинами.
При изучении случайной величины 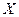 , часто из теоретических соображений удается установить вид распределения и по данным выборки необходимо оценить его численные параметры.
, часто из теоретических соображений удается установить вид распределения и по данным выборки необходимо оценить его численные параметры.
Например: если случайная величина имеет нормальное распределение, то для полного его определения необходимо оценить его математическое ожидание и среднее квадратическое отклонение.
Определение:статистическая оценка неизвестного параметра теоретического распределения- функция от наблюдаемых случайных величин 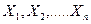 , т.е. также случайная величина
, т.е. также случайная величина  (
( 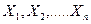 ), которая на различных реализациях выборки принимает конкретные значения
), которая на различных реализациях выборки принимает конкретные значения  ; ее значение служит оценкой неизвестного параметра теоретического распределения
; ее значение служит оценкой неизвестного параметра теоретического распределения  .
.
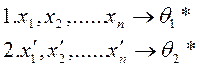
§2. Точечные и интервальные оценки. Доверительный интервал. Точность оценки. Доверительная вероятность (надежность).
Существует 2 вида оценок параметров распределения (числовых характеристик) изучаемого признака генеральной совокупности по данным выборки:
1. Точечная оценка неизвестного параметра 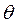 – это случайная функция
– это случайная функция  (
( 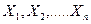 ), значение которой для любой реализации выборки принимают за приближенное значение параметра
), значение которой для любой реализации выборки принимают за приближенное значение параметра 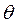 .
.
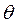 *(
*( 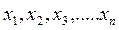 )
) 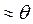
2. Интервальная оценка неизвестного параметра 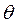 - это случайная функция
- это случайная функция  (
( 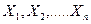 ) , такая, что :
) , такая, что :

Геометрически выражение (1) означает, что интервал с границами
( 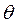 *-
*-  ;
; 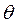 *+
*+  ) «накроет » неизвестный параметр
) «накроет » неизвестный параметр 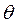 с вероятностью
с вероятностью  .
.
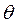 *-
*- 
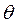
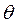 *
* 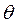 *+
*+ 
 (2)
(2)
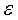
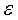
Сам интервал (2) называется доверительным интервалом.
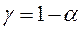 – доверительная вероятность оценки (надежность, коэффициент доверия)
– доверительная вероятность оценки (надежность, коэффициент доверия)
Числа Q*- 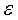 ; Q*+
; Q*+ 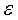 называются доверительными границами.
называются доверительными границами.
 - уровень значимости (существенности), который характеризует риск наступления события, что параметр
- уровень значимости (существенности), который характеризует риск наступления события, что параметр 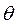 в интервале (2) не содержится.
в интервале (2) не содержится.
Доверительная вероятность( 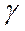 )- характеризует степень доверия к событию, что неизвестный (но не случайный) параметр
)- характеризует степень доверия к событию, что неизвестный (но не случайный) параметр 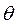 содержится внутри доверительного интервала.
содержится внутри доверительного интервала.
Чем более существенны последствия ошибки, что параметр 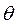 не содержится в доверительном интервале, тем меньшим уровнем значимости нужно задаваться.
не содержится в доверительном интервале, тем меньшим уровнем значимости нужно задаваться.
§3. Несмещенные, состоятельные и эффективные оценки.
Для того чтобы статистической оценке можно было доверять, она должна обладать некоторыми свойствами.
Статистическая оценка 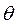 * называется несмещенной, если её математическое ожидание M(
* называется несмещенной, если её математическое ожидание M( 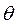 *) равно оцениваемому параметру
*) равно оцениваемому параметру 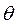 .
.
Несмещенность оценки означает отсутствие систематических ошибок в эксперименте (наблюдениях).
Статистическая оценка 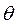 * называется состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е для любого достаточно малого числа
* называется состоятельной, если она сходится по вероятности к оцениваемому параметру, т.е для любого достаточно малого числа 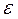 .
.
 Предел вероятности того, что оценка
Предел вероятности того, что оценка 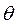 * отличается от параметра
* отличается от параметра 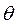 по абсолютной величине меньше чем на
по абсолютной величине меньше чем на 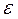 при ограниченном увеличение объема выборки равно 1.
при ограниченном увеличение объема выборки равно 1.
Замечание.
Из неравенства Чебышева следует (закон больших чисел), что несмещенная оценка, дисперсия которой 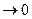 , при
, при  , является состоятельной.
, является состоятельной.
Статистическая оценка 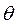 * называется эффективной, если при данном объеме выборки из всех возможных оценок она имеет наименьшую дисперсию.
* называется эффективной, если при данном объеме выборки из всех возможных оценок она имеет наименьшую дисперсию.
Замечание.
На практике не всегда удается добиться всех трех требований оценки. Из соображения практической удобности позволяют пользоваться не полностью адекватными оценками, но необходимо знать какими свойствами мы пренебрегаем.
§ 4. Точечная оценка генерального среднего по выборочной средней.
Пусть требуется изучить генеральную совокупность относительно количественного признака Х, имеем выборку 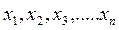 и будем рассматривать эту выборку как реализованную систему случайных величин,
и будем рассматривать эту выборку как реализованную систему случайных величин, 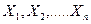 т.е. выборку следует понимать в 2-ух смыслах:
т.е. выборку следует понимать в 2-ух смыслах:
1.Как систему 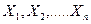 , n-независимых одинаково распределенных случайных величин, у каждой из которых закон распределения такой же, как у случайной величины Х (изучаемый признак).
, n-независимых одинаково распределенных случайных величин, у каждой из которых закон распределения такой же, как у случайной величины Х (изучаемый признак).
2. Как конкретную выборку 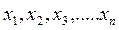 , где
, где
 - реализованная случайная величина
- реализованная случайная величина 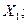
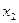 -реализованная случайная величина
-реализованная случайная величина 
 -реализованная случайная величина
-реализованная случайная величина 
Выберем в качестве оценки генерального среднего M(X)=a, среднее арифметическое случайных величин 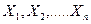 ,
,

(для конкретной реализации выборки значение 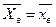 .)
.)
Найдем математическое ожидание
М(  т.к
т.к 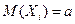
Вывод:
Случайная величина 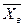 – это несмещенная оценка математического ожидания генеральной совокупности.
– это несмещенная оценка математического ожидания генеральной совокупности.
По теореме Чебышева для любого  ,
,
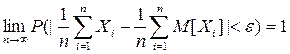 ,
,
По этой теореме, используя предыдущее равенство можно записать, что:
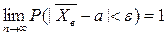 , т.е., по определению,
, т.е., по определению, 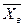 - состоятельнаяоценка
- состоятельнаяоценка 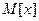
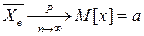
Если случайная величина распределения по нормальному закону
СВХ~N(a, 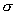 ), то оценка
), то оценка 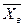 будет эффективной.
будет эффективной.
§ 5. Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии.
Пусть случайная величина Х- исследуемый признак.
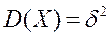
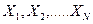 - выборка.
- выборка.
 -среднее значение квадратичных отклонений.
-среднее значение квадратичных отклонений.
Покажем, что выборочная дисперсия ( 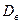 ) является смещенной оценкой генеральной дисперсии
) является смещенной оценкой генеральной дисперсии  .
.
Найдем математическое ожидание дисперсии
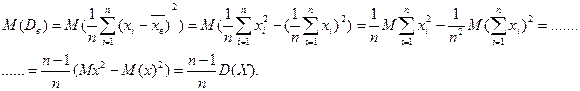
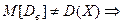
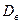 является смещенной оценкой генеральной дисперсии.
является смещенной оценкой генеральной дисперсии.
Для получения несмещенной оценки достаточно перейти к исправленной выборочной дисперсии:
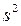 =
= 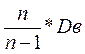 ; (
; ( 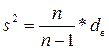 )
)
Очевидно, исправленная выборочная дисперсия является несмещенной оценкой генеральной дисперсии.
Покажем, что исправленная выборочная дисперсия является состоятельной оценкой генеральной дисперсии, т.е. для любого достаточно малого числа 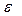 >0.
>0.
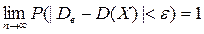
Т.е выборочная дисперсия является состоятельной оценкой генеральной дисперсии.
Замечание
Оценка 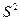 =
= 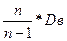 для генеральной совокупности не является эффективной, но для нормального распределения эта оценка является асимптотически эффективной, т.е. при (
для генеральной совокупности не является эффективной, но для нормального распределения эта оценка является асимптотически эффективной, т.е. при (  ) отношении дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице.
) отношении дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице.
§6. Метод моментов для точечной оценки параметра распределения.
В рамках этого метода предложенного К.Пирсоном, в качестве точечных оценок теоретических моментов рассматриваемого распределения берутся эмпирические, выборочные моменты того же порядка.
Можно показать, что начальные и центральные выборочные моменты являются состоятельными оценками соответствующих теоретических моментов.
Пусть известен вид плотности распределения, зависящей от двух неизвестных параметров  ;
; 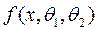 .
.
Требуется найти оценки этих параметров ( 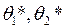 ) по данным выборки (
) по данным выборки ( 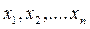 ). Для нахождения оценок этих параметров составляют два уравнения, которые получаются следующим образом: приравниваем начальные моменты 1-ого порядка и центральные моменты 2-ого порядка.
). Для нахождения оценок этих параметров составляют два уравнения, которые получаются следующим образом: приравниваем начальные моменты 1-ого порядка и центральные моменты 2-ого порядка.
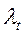 =
= 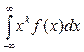 ; или
; или 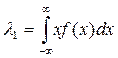 -теоретический начальный момент 1-ого порядка;
-теоретический начальный момент 1-ого порядка;
 ; или
; или 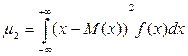 - теоретический центральный момент 2-ого порядка.
- теоретический центральный момент 2-ого порядка.
Эмпирические моменты:
1.Начальный момент:

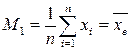
2.Центральный момент
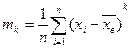
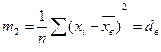
В общем случае, когда выборка это система случайных величин, то статистические моменты начальный и центральный тоже являются случайными величинами.  ,
, 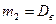



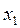 ,
, 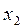 , ...,
, ..., 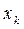 є основними. На них можна впливати з метою зміни значень критеріїв оптимізації (управління станом об'єкту оптимізації).
є основними. На них можна впливати з метою зміни значень критеріїв оптимізації (управління станом об'єкту оптимізації).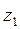 ,
, 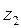 , ...,
, ..., 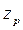 ) вимірюють в процесі дослідження, їх не змінюють цілеспрямовано (зазвичай можливість дії на них відсутня).
) вимірюють в процесі дослідження, їх не змінюють цілеспрямовано (зазвичай можливість дії на них відсутня).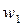 ,
, 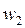 , ...,
, ..., 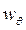 ) - неконтрольовані, вони недоступні для виміру, їх значення змінюються в часі випадковим чином.
) - неконтрольовані, вони недоступні для виміру, їх значення змінюються в часі випадковим чином. (признак), причем значение
(признак), причем значение 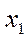 наблюдалось
наблюдалось 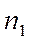 -раз, значение
-раз, значение 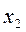 наблюдалось
наблюдалось 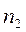 -раза,
-раза, 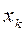 –
–  -раз и т.д.
-раз и т.д.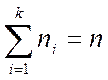
 ,
, 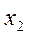 ,
, 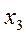 ,….
,…. 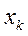 ,принято называть вариантами, а последовательность вариант, записанную в порядке возрастания - вариационным рядом.
,принято называть вариантами, а последовательность вариант, записанную в порядке возрастания - вариационным рядом. ,
, 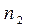 ,…
,…  называют частотами.
называют частотами. 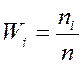 где
где 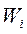 - относительная частота.
- относительная частота.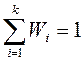
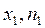 ), (
), ( 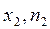 ),…..(
),…..(  ) или (
) или (  ),(
),(  )….(
)….(  ).
).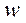 ) есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной
) есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной 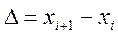 и высотами
и высотами 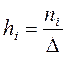 или
или 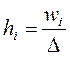 .
. .
.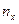 - число вариант,меньших
- число вариант,меньших  .
.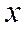 - любое действительное число.
- любое действительное число.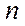 - объем выборки.
- объем выборки.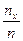 .
. меняется и относительная частота, т.е отношение
меняется и относительная частота, т.е отношение  , где
, где 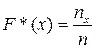
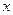 ) случайной величины
) случайной величины  , вычисленная по генеральной совокупности, т.е вероятность события
, вычисленная по генеральной совокупности, т.е вероятность события 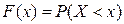 .
.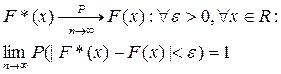
 , а исходную случайную величину –
, а исходную случайную величину – 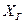 .
. .
. 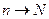 ), числовые характеристики случайной величины
), числовые характеристики случайной величины 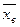 )-среднее арифметическое значений выборки:
)-среднее арифметическое значений выборки: ;
;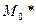 )- наиболее вероятное значение в выборке (варианта с наибольшей частотой);
)- наиболее вероятное значение в выборке (варианта с наибольшей частотой);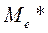 ) - значение случайной величины, приходящейся на середину вариационного ряда;
) - значение случайной величины, приходящейся на середину вариационного ряда;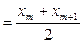 ;
; 
 ;
;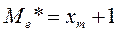 ;
; 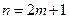 ;
;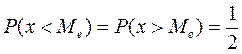 .
.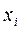 от
от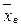
 ;
; ;
;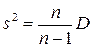 ;
; ;
;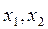 ), [
), [ 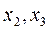 ), …..[
), …..[ 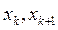 ) т.е
) т.е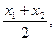
 …..
….. 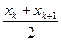 .
. также можно ввести числовые характеристики:
также можно ввести числовые характеристики: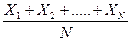 .
.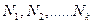 , причем (
, причем ( 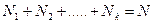 ), то
), то .
.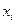 от генерального среднего
от генерального среднего 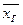 ,
,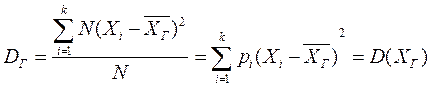
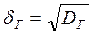
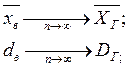
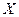 , сделана выборка объема n и получены значения
, сделана выборка объема n и получены значения 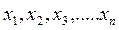 .
.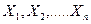 , распределение которых совпадает с распределением случайной величины
, распределение которых совпадает с распределением случайной величины  (
(  ; ее значение служит оценкой неизвестного параметра теоретического распределения
; ее значение служит оценкой неизвестного параметра теоретического распределения  .
.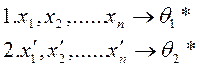
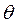 – это случайная функция
– это случайная функция 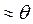

 ;
;  .
. (2)
(2)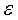
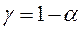 – доверительная вероятность оценки (надежность, коэффициент доверия)
– доверительная вероятность оценки (надежность, коэффициент доверия) - уровень значимости (существенности), который характеризует риск наступления события, что параметр
- уровень значимости (существенности), который характеризует риск наступления события, что параметр 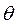 в интервале (2) не содержится.
в интервале (2) не содержится.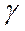 )- характеризует степень доверия к событию, что неизвестный (но не случайный) параметр
)- характеризует степень доверия к событию, что неизвестный (но не случайный) параметр 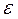 .
. Предел вероятности того, что оценка
Предел вероятности того, что оценка 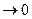 , при
, при  , является состоятельной.
, является состоятельной. - реализованная случайная величина
- реализованная случайная величина 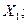
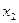 -реализованная случайная величина
-реализованная случайная величина 
 -реализованная случайная величина
-реализованная случайная величина 

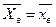 .)
.) т.к
т.к 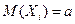
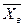 – это несмещенная оценка математического ожидания генеральной совокупности.
– это несмещенная оценка математического ожидания генеральной совокупности. ,
,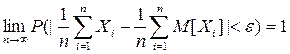 ,
,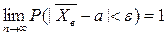 , т.е., по определению,
, т.е., по определению, 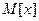
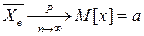
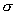 ), то оценка
), то оценка 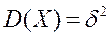
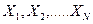 - выборка.
- выборка. -среднее значение квадратичных отклонений.
-среднее значение квадратичных отклонений.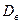 ) является смещенной оценкой генеральной дисперсии
) является смещенной оценкой генеральной дисперсии  .
.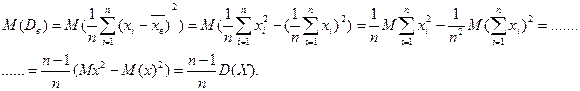
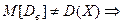
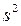 =
= 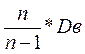 ; (
; ( 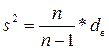 )
)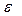 >0.
>0.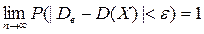
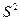 =
= 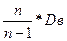 для генеральной совокупности не является эффективной, но для нормального распределения эта оценка является асимптотически эффективной, т.е. при (
для генеральной совокупности не является эффективной, но для нормального распределения эта оценка является асимптотически эффективной, т.е. при (  ) отношении дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице.
) отношении дисперсии этой оценки к минимально возможной дисперсии оценки стремится к единице. ;
; 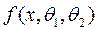 .
.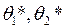 ) по данным выборки (
) по данным выборки ( 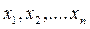 ). Для нахождения оценок этих параметров составляют два уравнения, которые получаются следующим образом: приравниваем начальные моменты 1-ого порядка и центральные моменты 2-ого порядка.
). Для нахождения оценок этих параметров составляют два уравнения, которые получаются следующим образом: приравниваем начальные моменты 1-ого порядка и центральные моменты 2-ого порядка.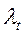 =
= 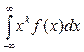 ; или
; или 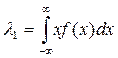 -теоретический начальный момент 1-ого порядка;
-теоретический начальный момент 1-ого порядка; ; или
; или 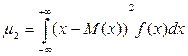 - теоретический центральный момент 2-ого порядка.
- теоретический центральный момент 2-ого порядка.
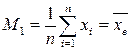
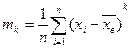
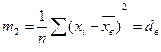
 ,
,