Лекція 1
 План лекції:
План лекції:
1.1. Етапи розв’язування задачі на ЕОМ
1.2. Поняття алгоритму
1.3. Властивості алгоритмів
1.4. Види алгоритмів
1.1. ЕТАПИ РОЗВ'ЯЗУВАННЯ ЗАДАЧІ НА ЕОМ
Від часу створення першої обчислювальної машини минуло більше п'яти десятиліть. За цей час кілька разів змінювалася елементна база ЕОМ, зменшилися розміри і споживані потужності, збільшилась швидкість обчислень, стало набагато зручніше з ними працювати. Впровадження й широке використання засобів обчислювальної техніки є одним з головних факторів прискорення науково-технічного прогресу в будь-якій країні світу. Стрімко зростає роль ЕОМ у всіх областях людської діяльності. Без використання швидкодіючих ЕОМ немислиме рішення завдань інтенсифікації економічного розвитку провідних галузей народного господарства.
Темпи науково-технічного прогресу, посилення ролі в значній мірі визначаються якістю й номенклатурою засобів обчислювальної техніки і їхнім програмним забезпеченням. Саме розвиток цих засобів забезпечує успіхи в автоматизації виробничих процесів, у розробці нових технологій, у підвищенні ефективності праці й керування. Широке й різноманітне застосування ЕОМ ставить усе більше високі вимоги до їхнього програмного забезпечення. Розробка програм і програмних комплексів здобуває характер індустріального виробництва. Значення програмного забезпечення важко переоцінити, тому що саме програми визначають і створюють «інтелект» комп'ютера. У той же час процес створення програм ставиться до однієї з найбільш складних сфер творчої діяльності людини, що вимагає більших зусиль і спеціальної технології розробки.
Не дивлячись на те, що номенклатура програмного забезпечення складає десятки тисяч програм, які торкаються всіх сторін людської діяльності, кожен фахівець може знайти в своїй області задачу, розв’язок якої хотів би автоматизувати.
Будь-яка задача, перш ніж вона може бути розв'язана на ЕОМ, проходить підготовчий шлях, який складається з декількох етапів.
· Спочатку потрібно сформулювати задачу, з’ясувати що вимагається знайти та що для цього відомо.
· Після цього необхідно подати математичне описання задачі. Для цього слід призначити імена відомим і невідомим змінним та постійним величинам, що характеризують явище, знайти формули чи рівняння, що їх зв’язують, або задати ці зв’язки у вигляді таблиць чи графіків. Це називають побудовою математичної моделі явища та формалізацією задачі.
· Далі розробляється або обирається з множини відомих метод розв'язування даної задачі та алгоритм його реалізації.
· На наступному етапі розробляється та налагоджується програма на алгоритмічній мові, або вибирається з множини вже існуючих програм.
· На етапі налагодження програми переконуються, що вона не містить синтаксичних і логічних помилок, застосувавши її до тестових завдань з заздалегідь відомими результатами.
· Нарешті програма запускається в дію, вводяться початкові дані і знаходяться результати, які аналізуються користувачем.
Важливим етапом є розробка алгоритму розв’язування задачі.
1.2. ПОНЯТТЯ АЛГОРИТМУ
Алгоритм – це послідовність дій над початковими даними та проміжними результатами необхідних для одержання кінцевого результату.
Алгоритм можна описати словами, у вигляді графічної схеми та програми на одній з мов програмування.
Графічне зображення алгоритму або блок-схема складається з блоків (графічних символів), що зв'язуються між собою направленими лініями. Читається схема зверху вниз, та зліва направо, тому стрілки, що вказують напрямок ліній можуть бути відсутніми.
Найбільш часто зустрічаються наступні блоки
1.3. ВЛАСТИВОСТІ АЛГОРИТМІВ
Алгоритм повинен мати наступні властивості:
Дискретність – процес рішення подається як послідовність кроків (етапів) і відбувається в часові дискретно.
Детермінованість(визначеність) – кожен крок повинен бути чітко визначеним і не повинен допускати довільного тлумачення.
Результативність – алгоритм повинен приводити до рішення задачі за скінчене число кроків.
Масовість – алгоритм рішення задачі розробляється в загальному виді, таким чином, щоб він міг бути застосованим для цілого класу задач, що різняться лише початковими даними.
1.4. ВИДИ АЛГОРИТМІВ
Розрізняють лінійні, розгалужені та циклічні алгоритми. Алгоритм вирішення будь-якої задачі може бути поданий як комбінація цих трьох вище названих.
Лінійний алгоритм характеризується одно направленим послідовним переходом від блоку до блоку по мірі їх виконання.
Приклад 1. Обчислити очікуване накопичення на внесок 2000 грн., який було зроблено клієнтом банку під 12 відсотків терміном на 5 років.
Формалізуємо постановку задачі. Позначимо очікуване накопичення змінною S, величину внеску – В, річний відсоток на внески – р, термін внеску – n.
Тоді результат можна обчислити за формулою S=B(1+p/100)n.
Блок-схему алгоритму обчислень відображено на рис. 1.1.
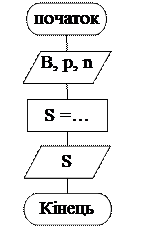
Рисунок 1.1. Блок-схема лінійного алгоритму
Розгалужений алгоритм має місце в тому разі, коли в залежності від виконання чи невиконання умови виконується одна чи друга дія.
Приклад 2. Визначити суму доплат за роботу в нічний час за формулою
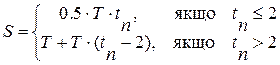
де Т-тарифна ставка, а tn – час відпрацьований вночі.
Блок-схема алгоритму може мати наступний вид
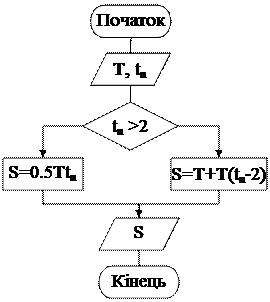
Рисунок 1.2. Приклад алгоритму розгалужених обчислень
Множинний вибір є узагальненням розгалуження, коли в залежності від значення змінної (І) виконується одна з багатьох дій.
Приклад 3. Обчислити денний заробіток робітника з погодинною оплатою враховуючи його розряд, якщо самі тарифи можуть змінюватися але коефіцієнти розрядної сітки остаються незмінними і визначаються таблицею
| Розряд
|
|
|
|
|
|
|
|
| Коефіцієнт
|
| 1.1
| 1.35
| 1.5
| 1.7
|
| 2.2
|
Позначимо денний заробіток літерою Z, розряд – r, кількість відпрацьованих робітником годин – n, тариф – Т, коефіцієнт тарифної сітки – k. Тоді Z=k*n*T, де значення k залежить від значення r.
Блок-схема алгоритму рішення задачі з використанням оператора множинного вибору відображена на рис. 1.3
Циклічний алгоритм передбачає багаторазове повторення якихось дій (обчислень, введення даних, виведення результатів, то що) при різних початкових умовах.
Цикли для яких число повторень наперед відоме або легко визначається називають арифметичними.
Цикли в яких число повторень невідоме, а повторення припиняються як тільки внаслідок них досягається виконання певної умови (умови виходу з циклу) називають ітераційними.

Рисунок 1.3. Блок-схема рішення задачі 3
Оператори які повторюються в циклі створюють тіло циклу. Перевірка умови може виконуватись до початку виконання тіла циклу (цикл типу Поки) або після виконання операторів тіла (цикл типу До).
Розглянемо приклад застосування арифметичного циклу.
Приклад 4. Використовуючи результат прикладу 3, підрахувати денні заробітки робітників цеху і сумарні витрати на оплату їх праці.
Особу робітника будемо визначати за його кодом-номером і у списку робітників. Для забезпечення масовості алгоритму позначимо число робітників літерою n. На початку рішення вкажемо це число, потім задаємо код робітника (почнемо з i=1). Витрати на оплату праці позначимо S. До початку обчислень вважатимемо S=0.
Нам потрібно n раз повторити одну і ту ж сукупність дій – обчислення заробітку робітника за його розрядом і тарифом, як це зроблено в прикладі 3. Щоб позбутись повторень, відповідну групу дій можна відобразити на блок-схемі окремим блоком і звертатись до нього, коли виникає потреба. Відособлена група операторів, яку можна повторювати багаторазово, звертаючись до неї з різних місць програми називається підпрограмою або процедурою. Щоб підпрограма при звертанні до неї виконувалась кожен раз з новими даними, її треба складати в загальному вигляді, а вихідні дані для роботи передавати в змінні підпрограми перед звертанням до неї.
Тож звертаємось до алгоритму створеного в прикладі 3 як до процедури Z. Оскільки робітники можуть мати різні професії, то введення значень тарифу, крім розряду і тарифного коефіцієнту, на кожному кроці оправдане. Отримане значення заробітку Z додаємо до S, накопичуючи суму, збільшуємо параметр циклу і (код робітника) на одиницю, перевіряємо умову і>n (умова того, що враховані заробітки всіх робітників цеху).
В разі її виконання припиняємо обчислення.
Блок-схема розглянутого алгоритму зображена на рис.1.4.
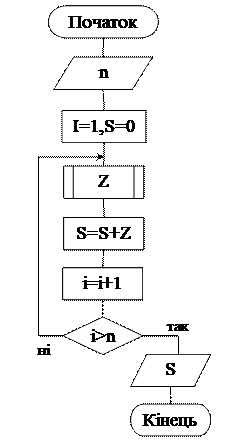
Рисунок 1.4. Блок-схема до Прикладу 4
На рис. 1.5 відображена блок-схема того ж алгоритму але з використанням модифікованого блоку циклу.
Модифікований блок циклу має вигляд
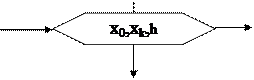
Текст, що відображено в блоці сповіщає про те, що параметр циклу змінюється від початкового значення x0 до кінцевого xk з кроком h. Якщо крок дорівнює 1, то його можна не вказувати.

Рисунок 1.5. Блок-схема до Прикладу 4
Приклад 5. Клієнт банку зробив внесок в 10000 грн. на термін 5 років. Банк гарантує 12% річних. Для показу динаміки зростання рахунку клієнта рік від року необхідно обчислити значення, які приймає накопичена сума на кінець кожного року.
Позначимо внесок літерою – В, річний відсоток – р, суму накопичення – S, поточний термін – і, термін внеску – n років.
Накопичення за n років визначається формулою S=B(1+p/100)n. таким чином задача зводиться до табулювання функції S(і)=B(1+p/100)і для і=1, 2,…, n. після обчислення значення функції відразу же будемо виводити його разом з відповідним поточним значенням і на екран. Тобто не будемо створювати масив значень функції в пам’яті машини. В протилежному випадку значення S(і) довелось би зберігати в окремому масиві (у виділеній для цього ділянці пам’яті), а для виведення на екран збережених у масиві S(і) значень необхідно було б створювати окремий цикл.
Алгоритм вирішення, розглянутої задачі, відображено на рис. 1.6.
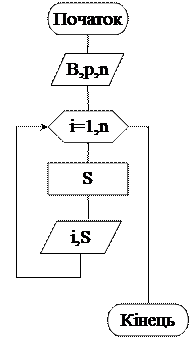
Рисунок 1.6. Блок-схема арифметичного циклу
Розглянемо приклад ітераційного циклу.
Приклад 6. В задачах теорії ймовірності і математичної статистики часто використовується інтегральна функція Лапласа
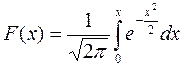
Обчислити її для довільного x з проміжку [0;5] з точністю до деякого малого числа ε.
З математики відомо, інтеграл Лапласа не може бути вираженим через елементарні функції, але для його обчислення з будь-якою точністю можна скористатись розкладанням цієї функції в ряд

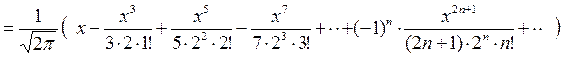
Маємо знакозмінний спадаючий ряд.
Якщо суму знакозмінного ряду замінити сумою його перших n членів, то похибка по модулю буде менше першого відкинутого члена.
Позначимо наближену суму через S, загальний член ряду
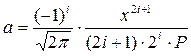 , де і=0,1,2,… , а Р=і!
, де і=0,1,2,… , а Р=і!
Алгоритм обчислення функції Лапласа з заданою точністю відображено на рис. 1.10.
На початку вказуємо значення змінної x, задаємо точність обчислення eps (наприклад, eps=0.001 або 0.000001) і початкові значення S=0, і=0, та P=i!=1
Цикл починаємо з обчислення значення a і накопичення суми (S=S+a).
Для обчислення і! використаємо підпрограму Fakt (рис. 1.7).Потім перевіряємо умову |a|<eps. Якщо вона не виконується, то збільшуємо на одиницю параметр циклу і ( і=і+1), обчислюємо Р=P*i, використовуючи те, що (i+1)!=і!*(i+1) та повертаємось до початку циклу. Коли досягнемо виконання умови, то вийдемо з циклу, виведемо наближене значення функції Лапласа і закінчимо програму.
Накопичена до цього сума S з точністю до |a|<eps, буде наближеним значенням функції Лапласа.
Блок-схема обчислення функції Лапласа зображена на рис. 1.7.
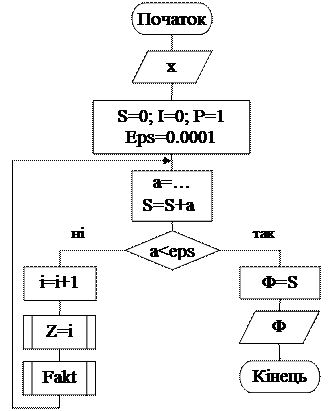
Рисунок 1.7. Блок –схема обчислення функції Лапласа.
Приклад 7. В партії з N деталей є n стандартних. Навмання відібрано m деталей. Знайти ймовірність того, що серед відібраних деталей рівно k стандартних.
Ймовірність визначається відношенням числа сприятливих випадків до загального числа усіх можливих випадків.
Загальне число можливих елементарних випадків дорівнює числу способів, якими можна вибрати m деталей з N деталей і рівне числу сполучень з N по m, що визначається формулою.
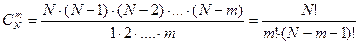
К стандартних деталей можна взяти з n стандартних деталей 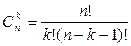 способами, при цьому останні m-k деталей повинні бути нестандартними, а взяти m-k нестандартних деталей з N-n нестандартних деталей можна
способами, при цьому останні m-k деталей повинні бути нестандартними, а взяти m-k нестандартних деталей з N-n нестандартних деталей можна 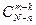 способами. Таким чином число сприятливих випадків становить
способами. Таким чином число сприятливих випадків становить
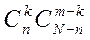 .
.
Ймовірність того, що серед m деталей рівно k стандартних
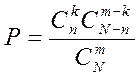 .
.
Обчислення числа розміщень  виділимо в окрему процедуру (в окремий блок), яка в свою чергу звертається до процедури обчислення Z!.
виділимо в окрему процедуру (в окремий блок), яка в свою чергу звертається до процедури обчислення Z!.
Блок-схема алгоритму обчислення Z! відображено на рис. 1.8.
Z! – це добуток всіх натуральних чисел від 1 до Z.
Спочатку вводимо значення Z, потім прирівнюємо початкове значення параметра Р рівним одиниці, а в циклі, в якому параметр циклу i змінюється від 1 до Z, обчислюємо наступні значення Р як добуток попереднього значення Р на чергове і (P=P*i).
Коли і перевищить значення Z виходимо з циклу і прирівнюємо результативну змінну останньому значенню Р (Fakt=P).
Алгоритм обчислення числа розміщень 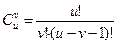 зображено на рис. 1.9.
зображено на рис. 1.9.
Позначимо через С1, С2, С3 відповідно u!,v! і (u-v-1)!. Для обчислення їх звертаємось до процедури Fakt, надаючи параметру Z одне з значень u, v та u-v-1 відповідно.
Розміщення обчислюємо за формулою 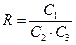
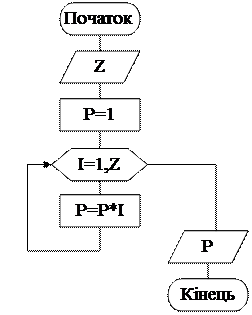
Рисунок 1.8. Блок-схема алгоритму обчислення Z!
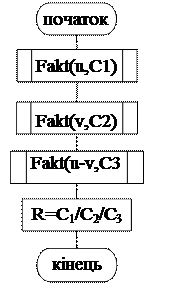
Рисунок 1.9. Блок-схема алгоритму обчислення числа сполучень  .
.
Алгоритм обчислення ймовірності при умові розглянутій у Прикладі 7 зображено на рис. 1.10.
Використовуємо формулу
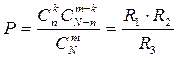 .
.
Для обчислення чисел сполучень R1,R2 ,R3 тричі звертаємось до процедури R, надаючи параметрам u, v відповідних значень.
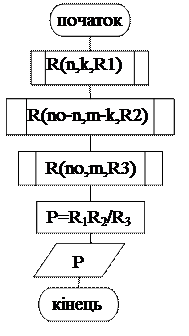
Рисунок 1.10. Блок-схема алгоритму обчислення ймовірності
Розглянемо приклад застосування подвійного циклу для роботи з двовимірним масивом.
Розв’язування більшості реальних задач на ЕОМ вимагає організації даних у вигляді масивів. Масивом називається впорядкована послідовність об’єктів, що позначається одним ім’ям. Кожен елемент масиву має свій номер – індекс. Щоб отримати доступ до елементу масиву потрібно вказати ім’я масиву і його індекс. Розрізняють одно-, дво- і багатовимірні масиви.
Прикладом одновимірного масиву може слугувати вектор X(x1,x2,x3). Елементами цього масиву є координати вектора. Прикладом двовимірного масиву може бути матриця. Елементи матриці aij впорядковуються за допомогою двох індексів – номера рядка i та номера стовпця j, на перетині яких стоїть елемент. Типовими є задачі знаходження суми елементів масиву, які задовольняють певним критеріям, знаходження найменшого чи найбільшого елементів масиву.
Приклад 8. Створити двомірний масив розміром т*n, знайти суму його додатних елементів, та знайти найбільший елемент масиву.
Для введення елементів матриці використовуємо подвійний цикл. Параметр зовнішнього циклу – номер рядка і, що змінюється від 1 до m, параметр вкладеного циклу – номер стовпця j, що змінюється від 1 до n.
Для обчислення суми S додатних елементів матриці спочатку надаємо змінній S значення 0 (S=0). Потім в подвійному циклі елементи матриці перевіряємо на виконання умови aij>0 і в разі так, накопичуємо суму S=S+aij.
Для знаходження найбільшого елемента спочатку зробимо припущення що Мах=a11, а потім в подвійному циклі порівнюємо Мах з наступними елементами і якщо виявиться більший, то його оголосимо максимальним, після чого продовжимо порівнювання. При виході з циклу Мах буде найбільшим елементом масиву. Для більшої компактності алгоритму можемо об’єднати накопичення суми і пошук максимуму з процесом введення елементів масиву. Алгоритм розв’язування задачі відображено на рис. 1.11.
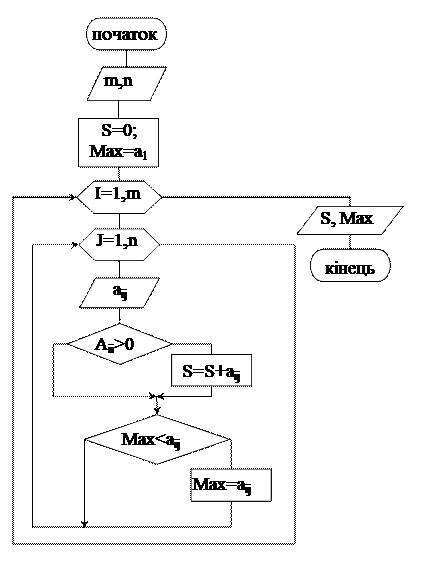
Рисунок 1.11. Блок-схема алгоритму обчислення суми елементів матриці та знаходження її найбільшого елемента.
На сьогодні існують технології розробки програм без використання блок-схем. Однак незалежно від цього на початковому етапі вивчення програмування доцільно при розробці алгоритму їх використовувати.
Найбільш поширеним описом алгоритмів рішення задач є програми написані на алгоритмічних мовах. Алгоритмічні мови високого рівня наближені до натуральної англійської мови, але мають обмежену кількість слів з яких будуються речення-рядки програм за строго визначеними правилами. Програма, складена на алгоритмічній мові, не може виконуватись ЕОМ безпосередньо, оскільки ЕОМ може виконувати тільки послідовності елементарних операцій, а команда в програмі на алгоритмічній мові може потребувати виконання десятків і сотень елементарних операцій, що зрозуміло людині, та недоступно ЕОМ. Переведення програми з алгоритмічної мови на машинну здійснюється самою ЕОМ за допомогою спеціальної програми, що називають транслятором. В програмі – трансляторі закладені всі правила алгоритмічної мови і способи перетворення різних конструкцій мови в послідовності елементарних команд зрозумілих машині. Тобто транслятор перетворює програму написану на алгоритмічній мові в програму на машинній мові. Найбільш поширеними мовами для ПК в наш час є Паскаль, Бейсик, С++, Java.
КОНТРОЛЬНІ ЗАПИТАННЯ
1. З яких етапів складається рішення задачі на ЕОМ?
2. Що таке алгоритм та яким чином можна його описати?
3. Що таке схема алгоритмів?
4. З яких блоків може складатися блок-схема алгоритму?
5. Яким чином читається алгоритм? Чи обов’язкова наявність стрілочок у графічній схемі алгоритму?
6. Які властивості повинен мати алгоритм?
7. Які існують правила розробки алгоритмів?
8. Які різновидності структур алгоритмів ви знаєте. Наведіть приклади.
9. Які цикли називаються арифметичними? Наведіть приклади.
10. Які цикли називаються ітераційними? Наведіть приклади.
11. Чим відрізняються лінійний, циклічний та розгалужений алгоритми?
12. Про який алгоритм можна сказати, що він має складену структуру?
13. Що таке масив? Які види масивів ви знаєте?
14. Надайте приклад одно- та двовимірного масивів.
15. Який опис алгоритмів рішення задач ви знаєте? Що таке алгоритмічна мова?


 План лекції:
План лекції:
 Введення, виведення
Введення, виведення

 Так Ні
Так Ні
 Підпрограма, процедура
Підпрограма, процедура
 Блок модифікації циклу
Блок модифікації циклу
 Сполучник
Сполучник
 Міжсторінковий сполучник
Міжсторінковий сполучник



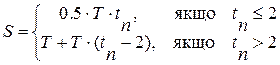



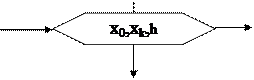


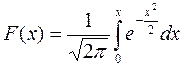

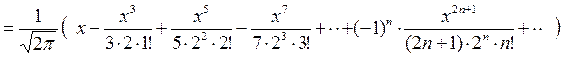
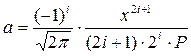 , де і=0,1,2,… , а Р=і!
, де і=0,1,2,… , а Р=і!
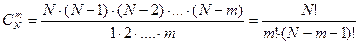
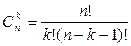 способами, при цьому останні m-k деталей повинні бути нестандартними, а взяти m-k нестандартних деталей з N-n нестандартних деталей можна
способами, при цьому останні m-k деталей повинні бути нестандартними, а взяти m-k нестандартних деталей з N-n нестандартних деталей можна 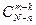 способами. Таким чином число сприятливих випадків становить
способами. Таким чином число сприятливих випадків становить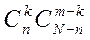 .
.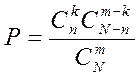 .
. виділимо в окрему процедуру (в окремий блок), яка в свою чергу звертається до процедури обчислення Z!.
виділимо в окрему процедуру (в окремий блок), яка в свою чергу звертається до процедури обчислення Z!.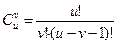 зображено на рис. 1.9.
зображено на рис. 1.9.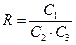


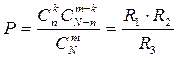 .
.
