Мова, аксіоми і правила висновку, повнота та несуперечність, правила відділення і підстановки, теорема дедукції та її наслідок, доведення методом від супротивного
Для логічного аналізу необхідно створити сукупність правил визначення істинності або хибності висловлень.
Довести те, що деяка формула логіки висловлень є тавтологією, можна, використовуючи таблицю істинності, еквівалентні перетворення формули, а також за допомогою дедуктивного висновку. На базі логіки висловлень створено формальну систему — обчислення висловлень,яка дозволяє за допомогою правил дедуктивного висновку перевірити, чи є задана формула загальнозначущою, а також одержати загальнозначущі формули логіки висловлень.
Насправді, існують різні формалізації логіки висловлень, тобто різні обчислення висловлень або за іншою термінологією різні формальні системи. Термін формальний означає, що об'єкти розглядаються без інтерпретації їх змісту, значення або сенсу. Операції над об'єктами проводяться за строгими формальними правилами, не розглядається значення сенсу проведених операцій.
Обчислення висловлень містить мову, систему аксіом і правила висновку.
Мова обчислення висловлень складається з правильно побудованих формул логіки висловлень.
Аксіомами обчислення висловлень є деяка множина загальнозначущих формул логіки висловлень.
Правила висновку дозволяють одержувати нові формули, які є істинними за умови істинності всіх засновків, що входять до правила.
Теорема 1
Теореми обчислення висловлень є тотожно істинними формулами.
Доведення. Теореми — це формули, які є логічним наслідком множини аксіом даного обчислення. Аксіоми обчислення висловлень є тотожно істинними формулами, а логічні наслідки тотожно істинних формул також є тотожно істинними (твердження 3, п. 5.3). Таким чином, теореми обчислення висловлень є тотожно істинними формулами, що і треба було довести.
Системи аксіом обчислення висловлень підбираються таким чином, щоб обчислення мало властивість повноти.
Повнота обчислення висловлень полягає в тому, що в даній системі є достатня кількість аксіом для того, щоб вивести будь-яку формулу логіки висловлень, яка є тотожно істинною.
Крім того, обчислення висловлень має властивість несуперечності.
Теорема 2. Несуперечність обчислення висловлень
Не існує формули А такої, що формули А і ØА є теоремами цього обчислення.
Доведення. Скористаємося методом від супротивного. Нехай правильно, що А і ØА одночасно є теореми цього обчислення. За законом суперечності хоча б одна з них не є загальнозначущою. З іншого боку, за теоремою 1 всі формули обчислення висловлень є загальнозначущими. Одержана суперечність доводить теорему.
Якщо жодну з аксіом системи обчислення висловлень не можна вивести з решти, застосовуючи правила висновку даної системи, то говорять, що система аксіом незалежна. Аксіоми обчислення висловлень підбираються таким чином, щоб вони були незалежні.
Крім правила відділення (Modus Ponens, п. 5.3), у обчисленні висловлень часто використовується так зване правило підстановки.
Правило підстановки
Нехай F1і F2— формули логіки висловлень, А — атомарна формула. Якщо F1(A) — формула, виведена в обчисленні висловлень, що містить атом А, то F1(В)— виведена формула, одержана заміною всіх входжень А у формулі F1на формулу F2.
Правило підстановки записується так:
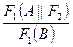 .
.
Правило підстановки виражає той факт, що якщо у тотожно істинній формулі всі входження будь-якого атома замінити на деяку формулу, то одержаний вираз залишиться тотожно істинним.
Приклад. Використовуючи правило підстановки і комутативний закон для диз'юнкції, довести загальнозначущість такої формули:
A Ú B Ù C ~ B Ú C Ú A.
Розв'язок. Запишемо тотожність, що відповідає комутативному закону для диз'юнкції:
A Ú D ~ D Ú А.
Визначимо підстановку — атомарну формулу D замінимо на (В Ú С):
A Ú (В Ù С) ~ (В Ù С) Ú А.
Опустивши дужки згідно з пріоритетом операцій, переконуємося в істинності вихідної формули.
Часто правило підстановки не згадують, а використовують його як очевидний факт, правильний для тотожностей. У цьому випадку аксіоми обчислення висловлень називають схемами аксіом,підкреслюючи те, що кожний атомарний символ у них може бути замінений на деяку формулу.
Опишемо дві формальні системи обчислення висловлень.
Система S1
І. Мова складається з правильно побудованих формул логіки висловлень, що містять операції {Ø, ®}. Алфавіт мови співпадає з алфавітом логіки висловлень і містить, крім символів перелічених логічних операцій, символи дужок і символи для позначення висловлень.
II. Аксіоми:
1. А ® (В ® А);
2. (А ® (В ® С))® ((А ® В) ® (А ® С));
3. (ØВ ® ØА) ® ((ØВ ® А) ® В).
III. Правила висновку:
1. Правило відділення (Modus Ponens);
2. Правило підстановки.
Система S2
I. Мова складається з правильно побудованих формул логіки висловлень, що містять операції {Ù, Ú, Ø, ®}. Алфавіт мови співпадає з алфавітом логіки висловлень і містить, крім символів перелічених логічних операцій, символи дужок і символи для позначення висловлень.
II. Аксіоми:
1. А ®(В ® А);
2. (А ® В) ® ((А ® (В ® С)) ® (А ® С));
3. (А Ù В) ® А;
4. (А Ù В) ® В;
5. А ® (В ® (А Ù В));
6. А ® (A Ú В);
7. B ® (A Ú В);
8. (A ® С) ® ((В ® С) ® ((A Ú В) ® С));
9. (А ® В) ® ((А ® ØВ) ® ØА);
10.ØØА ® А.
III. Правила висновку:
1. Правило відділення (Modus Ponens);
2. Правило підстановки.
Приклад. Довести вивідність формули А ® А в системі S1. Процедуру доведення проведемо покроково:
1. (А ® ((А ® А) ® А)) ® ((А ® (А ® А)) ® (А ® А)) — підстановка в аксіому 2 (А ® А) замість В, А замість С.
2. А ® ((А ® А) ® А)— підстановка в аксіому 1 (А®А) замість В.
3. (А ® (А ® А)) ® (А ® А)— за правилом 1, кроки 1, 2.
4. А ® (А ® А)— підстановка в аксіому 1 А замість В.
5. А ® А— за правилом 1, кроки 3, 4.
Доведення проведено.
Часто у математичних міркуваннях істинність твердження В доводять за припущенням істинності твердження А, після чого приходять до висновку, що правильне твердження «якщо А, то В». Такий прийом доведення є правильним і сформульований у такій теоремі. Спочатку введемо символ |— тавтології.
Теорема 3. Теорема дедукції
Якщо А1, ..., Аn, С|— В, то А1, ..., Аn|— С ® В. Зокрема, якщо А|— В, то |— А ® В.
Теорема 4. Наслідок з теореми дедукції
Із засновків А ® В, В ® С виводимо А ® С: А ® В, В ® С |— А ® С.
Приклад. Довести, що формула (ØА ® ØВ) ® ((ØА ® В) ® А) виведена в системі S2.
1. (ØА ® В) ® (ØА ® ØВ) ® ØØА) — підстановка в аксіому 9 ØА замість А.
2. (ØА ® В), (ØА ® ØB) |— ØØА— теорема 3, крок 1.
3. ØØА|— А — аксіома 10.
4. (ØА ® В), (ØА ® ØВ) |— А — теорема 4, крок 2, 3.
5. (ØА ® ØВ) |— (ØА ® В) ® А— теорема 3, крок 4.
6. |— (ØА ® ØВ) ® ((ØА ® В) ® А) — теорема 3, крок 5.
Доведення проведено.
Всі теореми обчислення висловлень зв'язані з розв'язком такої задачі: «чи випливає це твердження з деякої сукупності інших тверджень?» Тобто, доводиться тотожна істинність формули виду А ® В, що можна здійснити кількома методами. Замість прямого логічного висновку формули В з формули А часто виявляється зручним довести суперечність формули А ® ØВ, тим самим довівши істинність формули А® В. В формулі А ® ØВ присутнє заперечення наслідку ØВ, тому такий метод доведення називається доведенням від супротивного.
Дві схеми доведення методом від супротивного
1. (А Ù ØВ) ®(С Ù ØС) º А ® В— якщо з припущення, що А — правильно, а В — неправильно, виходять два суперечних один одному висловлень, то це означає, що з А виходить В (див. твердження 1, п. 5.3).
2. ØВ ®ØА º А ® В — якщо з припущення, що В — неправильно, виходить, що А неправильно, то це означає, що з А виходить В. Таким чином, довівши істинність лівої частини однієї з наведених схем, доводять істинність висловлення А ® В.
Запитання
1. Що являє обчислення висловлень?
2. Поясніть поняття мови, аксіом і правил висновку обчислення висловлень.
3. Що є теоремами обчислення висловлень?
4. В чому полягає повнота і несуперечність обчислення висловлень?
5. Дайте визначення незалежній системі аксіом.
6. Назвіть правила висновку, які найбільш часто застосовуються під час побудови обчислення висловлень?
7. Сформулюйте теорему дедукції та її наслідок.
8. В чому полягає метод доведення від супротивного?
9. Дайте порівняльну характеристику двом схемам доведення від супротивного.
Завдання
1. Нехай А — «дверний замок зламаний», В — «вхідні двері відкриті ». Випишіть відповідний логічний висновок за правилом Modus Ponens.
2. Перевірте правильність таких висновків:
а)  ;
;
б) 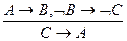 ;
;
в) 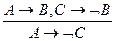 ;
;
г) 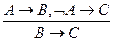 .
.


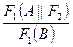 .
. ;
;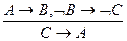 ;
;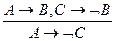 ;
;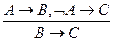 .
.