Особливості застосування теорії масового
Теорія масового обслуговування на основі теорії ймовірностей досліджує математичні методи кількісного оцінювання процесів масового обслуговування.
Теорія масового обслуговування розглядає ймовірнісні моделі реальних систем масового обслуговування (СМО) і використовується для мінімізації витрат у сферах обслуговування, виробництва, торгівлі. При цьому враховуються три фактори:
1) частота зміни кількості клієнтів або вимог;
2) імовірність значного попиту покупців;
3) спосіб визначення витрат очікування і поліпшення обслуговування.
Основні елементи системи масового обслуговування представлені на рисунку 6.1.
Вхідний потік Канали Вихідний
вимог ® обслуговування потік ®
® Черга ® ______________ ® ®
® ______________ ®
Рис. 6.1. Основні елементи системи масового обслуговування
Наприклад, надходження заявок на ремонт устаткування – вхідний потік; очікування ремонту – черга; ремонтні бригади – канали обслуговування; відремонтоване устаткування – вихідний потік.
У таблиці 6.1 наведена класифікація систем масового обслуговування.
За наявності одного каналу обслуговування СМО називається одноканальною, а якщо їх декілька – багатоканальною.
Таблиця 6.1 – Класифікація систем масового обслуговування
| Класифікаційні ознаки
| Види СМО
|
| Кількість каналів
| - одноканальні
- багатоканальні
|
| Включення вимог до системи
| - замкнені
- розімкнені
|
| Допустимість і характер формування черги
| - обслуговування з відмовами
- з необмеженою чергою
- змішаного типу
|
| Кількість процесів обслуговування
| - однофазні
- багатофазні
|
Якщо джерела вимог уключені до системи, вона називається замкненою, інакше – розімкненою.
Система обслуговування з відмовами має місце за умови неможливості формування черги. Вимога, яка прийшла в момент, коли всі канали зайняті, отримує відмову і не буде задоволена. Система масового обслуговування з необмеженою чергою є структурою, у якій дозволяється черга необмеженої довжини. У такій системі вимоги, які надійшли, будуть задоволені, хоча час очікування може бути досить тривалим. У СМО змішаного типу можливі різні обмеження, наприклад, на максимальну довжину черги, час перебування вимоги в черзі тощо.
Якщо декілька систем з’єднані послідовно, таким чином, щоб вимоги, котрі задоволені в одній системі, переходили до наступної, виникає багатофазна СМО (наприклад, послідовна обробка деталей на декількох видах обладнання), в протилежному випадку система однофазна.
Основне завдання теорії масового обслуговування – виявити залежність показників ефективності системи від характеру вхідного потоку, дисципліни й обмеження черги, кількості, продуктивності та умов функціонування каналів із метою наступної оптимізації СМО. В якості критерію оптимальності застосовують максимум прибутку від експлуатації системи; мінімум сумарних втрат, пов’язаних із простоєм каналів; мінімум вимог у черзі і виходів вимог, які не обслуговувались; задану пропускну здатність тощо.
Отже, тип задачі масового обслуговування визначається за такими ознаками:
1) характеристикою вхідного потоку;
2) часом обслуговування вимог;
3) числом каналів обслуговування;
4) порядком утворення черги вимог та обслуговування;
5) характеристикою вихідного потоку.
У системі управління виробництвом, як правило, необхідно вміти кількісно оцінити ефективність функціонування СМО з очікуванням. Для цього розраховуються середні значення параметрів:
1) кількість вимог у черзі та системі;
2) час очікування вимог у черзі;
3) число незайнятих каналів обслуговування;
4) коефіцієнти простою в черзі та системі;
5) коефіцієнти простою каналів обслуговування.
Розглянемо наступний приклад.
У цеху 7 однотипних устаткувань, які працюють незалежно одне від одного. Неполадки, які виникають в устаткуванні, мають випадковий характер і розподіляються за законом Пуассона. Протягом однієї години в середньому виходить з ладу 2 одиниці устаткування. Ці неполадки ліквідовуються одним механіком, який може обслужити протягом однієї години 8 вимог.
Необхідно розрахувати: коефіцієнти простою вимог у черзі та системі, коефіцієнт простою механіка та середній час очікування вимог у черзі.
Розв’язання
1. Відповідно до умови задачі маємо:
s = 1 – кількість каналів обслуговування (один механік);
l = 2 – інтенсивність вимог (вихід із ладу 2-х одиниць
устаткування за годину);
m = 8 – середня кількість вимог, що обслуговуються одним
каналом за одиницю часу;
т = 7 – величина, якою обмежена кількість вимог у системі
(7 одиниць устаткування).
2. Знайдемо інтенсивність обслуговування:
(6.1)
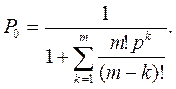 3. Знайдемо ймовірність того, що в системі немає жодної вимоги:
3. Знайдемо ймовірність того, що в системі немає жодної вимоги:
(6.2)
Таким чином, імовірність того, що в системі не буде жодної вимоги або все устаткування працюватиме, буде 0,063.
4. Знайдемо ймовірність того, що в системі знаходиться k вимог:
1 £ k £ m (6.3)
Pk = (7-k+1)´0,25´Рk-1, k=1,2,...,7.
Р1=(7-1+1)´0,25´0,63=0,110; Р5=(7-5+1)´0,25´0,206=0,154;
Р2=(7-2+1)´0,25´0,110=0,165; Р6=(7-6+1)´0,25´0,154=0,077;
Р3=(7-3+1)´0,25´0,165=0,206; Р7=(7-7+1)´0,25´0,077=0,019.
Р4=(7-4+1)´0,25´0,206=0,206;
5. Визначимо математичне сподівання кількості вимог у черзі (середня довжина черги):
(6.4)
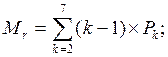 (6.5)
(6.5)
Мr = Р2 + 2Р3 + 3Р4 + 4Р5 +5Р6 + 6Р7 = 0,165 + 2´0,206 + 3´0,206 +
+ 4´0,154 + 5´0,077 + 6´0,019 = 2,31.
Отже, в середньому в черзі простоює 2,31 вимог.
6. Визначимо коефіцієнт простою вимог у черзі:
(6.6)
Тобто 33% робочого часу через неполадки устаткування простоює в черзі, чекаючи на обслуговування.
7. Визначимо математичне сподівання кількості вимог у системі (в черзі та в обслуговуванні):
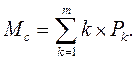 (6.7)
(6.7)
Мс = Р1 + 2Р2 + 3Р3 + 4Р4 +5Р5 + 6Р6 + 7Р7 = 0,11 + 2´0,165 +
+ 3´0,206 + 4´0,206 + 5´0,154 + 6´0,077 + 7´0,019 = 3,247.
Таким чином, у середньому в черзі та в обслуговуванні простоює 3,247 устаткування.
8. Визначимо коефіцієнт простою вимог у системі:
(6.8)
Тобто 46% робочого часу через неполадки устаткування простоює в черзі та в обслуговуванні.
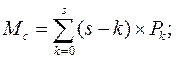 9. Визначимо математичне сподівання простою каналів обслуговування в системі:
9. Визначимо математичне сподівання простою каналів обслуговування в системі:
(6.9)
10. Визначимо коефіцієнт простою каналів обслуговування:
(6.10)
Таким чином, у середньому механік простоює 6,3% робочого часу, що свідчить про його високу завантаженість.
11. Знайдемо середній час очікування вимог у черзі:
(6.11)
Як бачимо, при існуючій організації проведення ремонтних робіт устаткування велику частину робочого часу витрачають на усунення неполадок, що призводить до значних економічних витрат. Зменшити витрати можна за допомогою збільшення кількості каналів обслуговування, тобто кількості механіків. Таким чином, виникає задача багатоканальної системи обслуговування.
Припустимо, що в цеху працюють два механіки з однаковою продуктивністю. Вхідні параметри системи залишаються незмінними.
а0 = 1, s = 2,
Р = l¸m = 2¸16 = 0,125.
(6.12)
Р1 = а1´Р0 = 0,37441; Р2 = а2´Р0 = 0,14041; Р3 = а3´Р0 = 0,0439;
Р4 = а4´Р0 = 0,011; Р5 = а5´Р0 = 0,00206; Р6 = а6´Р0 = 0,00026;
Р7 = а7´Р0 = 0,00002.
Обчислимо значення Мr, Мс і Мs:
Коефіцієнт простою устаткування в очікуванні ремонту:
Коефіцієнт простою устаткування в системі:
Коефіцієнт простою механіків:
Середній час очікування вимог у черзі:
Отже, використання на ремонті додатково ще одного механіка дозволить більш ефективно використовувати у виробничому процесі наявний парк устаткування. В той же час 61,5% свого робочого часу механіки будуть простоювати. Одержані дані можуть бути використані для поліпшення організації виробничого процесу.
Для визначення оптимальної кількості каналів обслуговування послідовність дій буде наступною:
1. Для заданої системи масового обслуговування послідовно розглядається різна кількість каналів обслуговування (s=1,2,..,п).
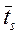 2. Для кожної кількості каналів розраховуються основні параметри систем обслуговування, в тому числі середній час простою вимоги в системі ( ).
2. Для кожної кількості каналів розраховуються основні параметри систем обслуговування, в тому числі середній час простою вимоги в системі ( ).
3. Встановлюється середня вартість витрат (СТ) унаслідок простою вимог за одиницю часу.
4. Визначаються затрати на втримання одного каналу обслуговування (СК) за одиницю часу.
5. Розраховується величина втрат, пов’язана з простоєм вимог при кількості каналів S за період T:
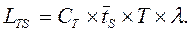
(6.13)
6. Обчислюються сумарні затрати на утримання S каналів обслуговуванняза період T:
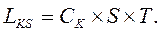 (6.14)
(6.14)
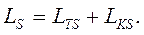 7. Знаходяться сумарні витрати в системі обслуговування при різній кількості каналів:
7. Знаходяться сумарні витрати в системі обслуговування при різній кількості каналів:
(6.15) 8. Вибирають оптимальні витрати (LS ® min), яким відповідає оптимальне значення числа каналів обслуговування.
Зробимо розрахунок оптимального числа механіків за даними вищенаведеного прикладу (табл. 6.2).
Таблиця 6.2 – Розрахунок оптимального значення числа
каналів обслуговування (кількості механіків)
| №
з/п
| Показники
| Кількість механіків
|
|
|
|
| 1.
| Середній час простою устаткування, год.
| 0,307
| 0,0059
|
| 2.
| Середньогодинна продуктивність одиниці
устаткування, грн.
|
|
|
| 3.
| Середня величина недоданої продукції у зв’язку з простоєм устаткування, грн. (п.1 х п.2)
|
153,50
|
2,95
|
| 4.
| Середньогодинна ставка оплати механіка, грн.
|
|
|
| 5.
| Сума заробітної плати механіків за зміну, грн.
(п.4 х 8 х кількість механіків)
|
|
|
| 6.
| Усього витрат, грн. (п.3 + п.5)
| 193,50
| 82,95
|
Розрахунок показує, що мінімальна сума витрат досягається за умови утримання двох механіків.



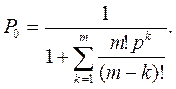 3. Знайдемо ймовірність того, що в системі немає жодної вимоги:
3. Знайдемо ймовірність того, що в системі немає жодної вимоги: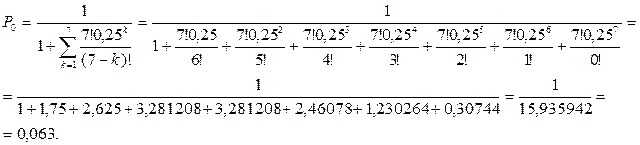
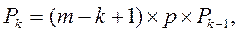

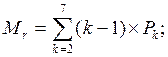 (6.5)
(6.5)
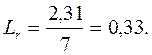
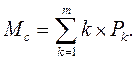 (6.7)
(6.7)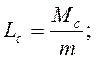
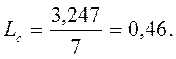
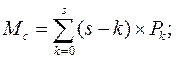 9. Визначимо математичне сподівання простою каналів обслуговування в системі:
9. Визначимо математичне сподівання простою каналів обслуговування в системі: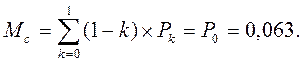
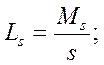
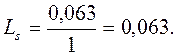
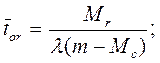
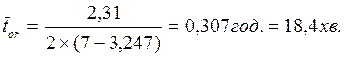
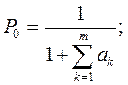
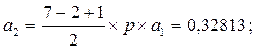
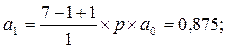
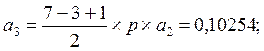
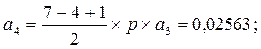
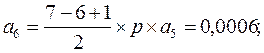
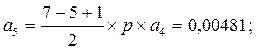
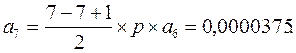
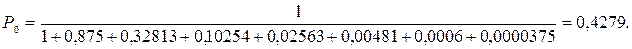
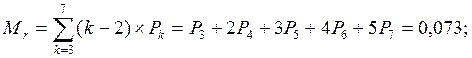
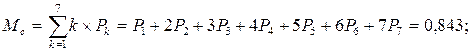
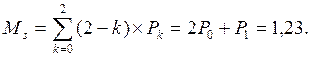
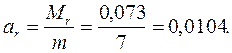
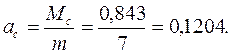

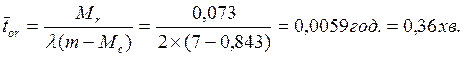
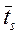 2. Для кожної кількості каналів розраховуються основні параметри систем обслуговування, в тому числі середній час простою вимоги в системі ( ).
2. Для кожної кількості каналів розраховуються основні параметри систем обслуговування, в тому числі середній час простою вимоги в системі ( ).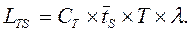
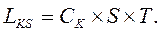 (6.14)
(6.14)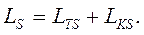 7. Знаходяться сумарні витрати в системі обслуговування при різній кількості каналів:
7. Знаходяться сумарні витрати в системі обслуговування при різній кількості каналів: