Одним з важливих напрямків сучасної нелінійної динаміки є дослідження детермінованого або динамічного хаосу в нелінійних системах різної фізичної природи. Траєкторії таких систем демонструють випадкову поведінку, яка не пов'язана з присутністю будь-яких зовнішніх випадкових сил або з статистичною невизначеністю систем з великим числом ступенів свободи. Динамічний хаос є внутрішньою властивістю нелінійних систем. Загалом він обумовлений експоненціальною чутливістю фазових траєкторій до як завгодно слабкого збурювання початкових умов. Починаючи з робіт А. Пуанкаре, за допомогою парадигми динамічного хаосу закріпився новий погляд на проблеми класичної та небесної механіки.
Принциповою метою теорії динамічного хаосу є вивчення особливостей регулярної та хаотичної динаміки у фазовому просторі динамічних систем, обчислення їх динамічних і статистичних характеристик, з'ясування типових механізмів і сценаріїв переходу до хаосу. Дотепер ці питання глибоко розроблені для неперервних (або гладких) динамічних систем. Останні описуються диференціальними рівняннями або точковими відображеннями, праві частини яких не мають особливостей (розривів). Динамічні системи з особливостями вивчені ще недостатньо, хоч вони всюди зустрічаються. У певному відношенні їх навіть більше, ніж гладких систем, тому що розривних функцій за категорією Бера “більше”, ніж неперервних. В даній роботі будемо досліджувати складні системи без розривів та динаміку нелінійних систем без заданих математичних моделей (на основі динаміки часових рядів) та із заданими математичними моделями.
Розглянемо динамічні системи докладніше. Якщо величини х1, х2, ..., xn – спостереження точки х в n-вимірному просторі за рівні проміжки часу, то отримаємо наочне геометричне представлення стану динамічної системи в цій точці. Таку точку назвемо фазовою точкою, а простір станів – фазовим простором динамічної системи. Зміні стану системи в часі відповідає рух фазової точки вздовж деякої лінії, що називається фазовою траєкторією або просто траєкторією.
Нехай математичною моделлю деякої динамічної системи є система звичайних диференціальних рівнянь.
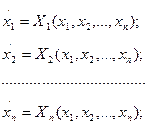 (1.2)
(1.2)
У фазовому просторі системи правими частинами рівняння (1.2) породжується векторне поле швидкостей, яке співставляє кожній точці х, що виходить з неї, вектор:
 .
.
Модуль цього вектора чисельно дорівнює швидкості руху фазової точки по траєкторії. Сам вектор в кожній точці х направлений по дотичній до фазової траєкторії.
Таким чином, динамічна система (1.2) може бути записана у векторній формі 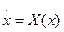 , (1.3)
, (1.3)
де  ,
, 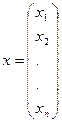 ,
, 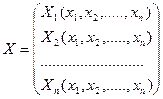 - відповідні вектори і вектор-функція розмірності n.
- відповідні вектори і вектор-функція розмірності n.
В теорії диференційних рівнянь доведено що в системі (1.2) існує три типи траєкторій:
1. Положення рівноваги, що складається з однієї нерухомої точки у фазовому просторі.
2. Цикли, які є замкнутими лініями у фазовому просторі.
3. Траєкторії без самоперетинів (незамкнені траєкторії).
За енергетичною ознакою динамічні системи діляться на консервативні та дисипативні. Консервативні системи характеризуються незмінним у часі запасом енергії. Динамічні системи, енергія яких зменшується з плином часу внаслідок тертя, розсіювання та інших факторів, називаються дисипативними.
Серед динамічних систем особливу роль відіграють системи, у яких можливі ті чи інші коливання. Такі динамічні системи називають коливальними.
Припустимо, що динамічна система описується системою звичайних диференціальних рівнянь (1.2):
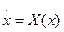 , де х – вектор з компонентами
, де х – вектор з компонентами 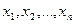 , а Х(х) – вектор-функція з компонентами,
, а Х(х) – вектор-функція з компонентами, 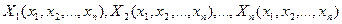 .
.
Нехай початкова умова системи стану (1.2) задається вектором х0 з компонентами  . Припустимо, що у фазовому просторі динамічної системи існує дві множини
. Припустимо, що у фазовому просторі динамічної системи існує дві множини 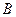 та
та  . Причому В – сукупність усіх точокх0 фазового простору для яких
. Причому В – сукупність усіх точокх0 фазового простору для яких  при
при 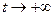 або
або 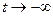 . В цьому випадку множина А називається граничною множиною динамічної системи.
. В цьому випадку множина А називається граничною множиною динамічної системи.
Розглянемо можливі типи граничних множин дисипативної динамічної системи, які можуть існувати в обмеженій області фазового простору.
Якщо всі точки х0 Î В прямують до А при 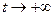 , то гранична множина є притягаючою і називається аттрактором. Відповідно множина В називається басейном тяжіння аттрактора.
, то гранична множина є притягаючою і називається аттрактором. Відповідно множина В називається басейном тяжіння аттрактора.
Якщо всі точки х0 Î В прямують до А при 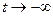 , то гранична множина є відштовхуючою і називається репеллером.
, то гранична множина є відштовхуючою і називається репеллером.
Множина А може складатися з двох підмножин, 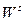 і
і 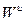 причому точки, які належать
причому точки, які належать 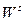 , прямують до А в прямому часі, в той же час точки, які належать
, прямують до А в прямому часі, в той же час точки, які належать 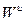 , прямують до А в зворотному часі. В цьому випадку А називається сідловою множиною або просто сідлом. Множини
, прямують до А в зворотному часі. В цьому випадку А називається сідловою множиною або просто сідлом. Множини 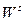 і
і 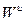 називаються відповідно стійким і нестійким різновидом сідла.
називаються відповідно стійким і нестійким різновидом сідла.
Простішою граничною множиною динамічної системи, яка складається з однієї точки, є положення рівноваги. Воно може бути аттрактором (стійкий вузол, стійкий фокус), репеллером (нестійкий вузол, нестійкий фокус) або сідлом. Причому у сідла стійким і нестійким різновидом є відповідно його стійка і нестійка сепаратриса. На малюнку 2 показані, зліва направо, аттрактор (стійкий фокус), репеллер (нестійкий фокус) і сідло.

Мал. 2. Положення рівноваги: аттрактор, репеллер і сідло
Зауважимо, що точка типу центр не є ні аттрактором, ні репеллером, ні сідлом, оскільки відсутня будь-яка множина точок, які наближаються до центру в прямому або зворотному часі. Точка типу центр — це особливий випадок граничної множини, для якої А = В.
У свою чергу, граничний цикл динамічної системи буде аттрактором, якщо він стійкий, і репеллером, якщо він цілком нестійкий. Напівстійкий граничний цикл є сідлом і називається сідловим. На мал. 3 зображені зліва направо: граничний цикл, який є аттрактором, граничний цикл, який є репеллером і сідловий граничний цикл.
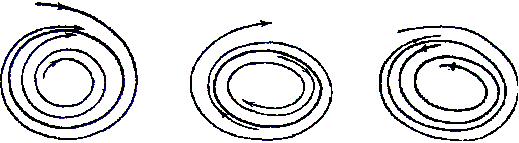
Мал.3. Граничні цикли: аттрактор, репеллер і сідловий
Таким чином, аттрактор – це гранична множина у фазовому просторі, до якого притягуються всі інші траєкторії з басейну тяжіння. Замітимо, що аттрактори існують тільки в дисипативних системах.
Рух в дисипативних системах доцільно розділити на два класи: клас перехідних, нестаціонарних рухів, які відповідають процесу переходу від початкової до граничної множини станів, і клас сталих, стаціонарних рухів, фазові траєкторії яких належать граничним множинам. Часто точну межу між цими класами рухів провести неможливо. Ця межа залежить від точності обчислень, що проводяться, при рішенні конкретної задачі.
В загальній теорії динамічних систем доведено, що диссипативная динамічна система може мати наступні типи аттракторов:
1) положення рівноваги (крапки у фазовому просторі);
2) граничні цикли (замкнуті лінії у фазовому просторі);
3) квазіперіодичні аттрактори (тороїдальні поверхні у фазовому просторі).
Вище перераховані аттракторы називаються регулярними. Їм відповідають повністю передбачені в часі рухи дисипативних динамічних систем.
Довгий час вважалося, що тільки такі типи аттракторов існують в динамічних системах. Проте в 60-х роках минулого століття були відкриті абсолютно нові типи аттракторів у динамічних системах. Виявилося, що рух повністю визначеної (детермінованої) динамічної системи може стати абсолютно не передбачуваним (хаотичним). Причому, що особливо важливо, ця непередбачуваність пояснюється властивостями самої динамічної системи, а не якою-небудь зовнішньою хаотичною дією. Проте, при всій своїй непередбачуваності, такі рухи мають ряд чітких кількісних і якісних закономірностей, що істотно відрізняє їх від класичних стаціонарних випадкових процесів. Тому для позначення таких типів рухів динамічних систем став використовуватись термін – «детермінований хаос». У свою чергу, для рухів, які описуються регулярними аттракторами, став вживатися термін – «порядок».
Математичними образами детермінованого хаосу у фазовому просторі є складним чином влаштовані притягуючі множини, траєкторії точок яких, не належать ні до одного типу регулярних аттракторів. Фазові траєкторії представляються у вигляді нескінченної лінії, яка ніде не перетинається, не залишає при 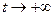 замкнуту область і не притягується до регулярних аттракторам. Точка, яка зображується час від часу повертається в окіл довільно вибраного на траєкторії початкового стану, проте ці повернення не передбачувані і мають вигляд випадкової послідовності. Такі аттрактори називаються дивними (хаотичними). Отже, з одного боку, маємо непередбачуваність положення зображуваної точки траєкторії на аттракторі в заданий момент часу, а з іншого боку – передбачуваність, оскільки точно відомо, що ця точка належить аттрактору.
замкнуту область і не притягується до регулярних аттракторам. Точка, яка зображується час від часу повертається в окіл довільно вибраного на траєкторії початкового стану, проте ці повернення не передбачувані і мають вигляд випадкової послідовності. Такі аттрактори називаються дивними (хаотичними). Отже, з одного боку, маємо непередбачуваність положення зображуваної точки траєкторії на аттракторі в заданий момент часу, а з іншого боку – передбачуваність, оскільки точно відомо, що ця точка належить аттрактору.
Практично перший хаотичний аттрактор був побудований Е. Лоренцем в 1963 р.


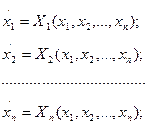 (1.2)
(1.2) .
.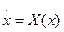 , (1.3)
, (1.3) ,
, 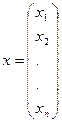 ,
, 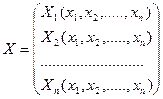 - відповідні вектори і вектор-функція розмірності n.
- відповідні вектори і вектор-функція розмірності n.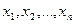 , а Х(х) – вектор-функція з компонентами,
, а Х(х) – вектор-функція з компонентами, 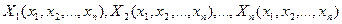 .
. . Припустимо, що у фазовому просторі динамічної системи існує дві множини
. Припустимо, що у фазовому просторі динамічної системи існує дві множини 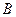 та
та  . Причому В – сукупність усіх точокх0 фазового простору для яких
. Причому В – сукупність усіх точокх0 фазового простору для яких  при
при 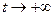 або
або 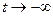 . В цьому випадку множина А називається граничною множиною динамічної системи.
. В цьому випадку множина А називається граничною множиною динамічної системи.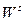 і
і 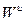 причому точки, які належать
причому точки, які належать 
