Ще одним складним типом є рекурсивні структури. Ітерація - це виконання якого-небудь процесу, що повторюється, до тих пір, поки не буде задоволена деяка умова. Причому, кожного разу виконання проводиться повністю, перевіряється умова і якщо вона не задовільняється, починається нове виконання.
На відміну від ітерації, рекурсія характеризується самовикликанням процесу, який виконується. Виконання не здійснюється повністю перед перевіркою умови, але перевірка умови входить в процес виконання, і при негативному результаті перевірки потрібно виконати все спочатку вже в якості підпрограми для ще не виконаної до кінця початкової програми. В якості ілюстрації рекурсивних структур можна розглянути наступне речення: "Я сказав, що ви думаєте, що він дуже розумний". Рекурсія визначається в деякій мірі через саму себе. Дану аналогію можна розповсюджувати на структури даних, що відповідають рекурсивним процедурам. Значення такого типу повинні містити більше однієї компоненти, що належить до того ж типу даних, що і саме значення, подібно до того, як рекурсивна процедура може викликати себе рекурсивно в своєму ж власному тілі, більш ніж з одного місця. Зручніше всього таку структуру визначати так, щоб ім'я типу що визначається, вживалось в середині свого особистого визначення, або для взаємно-рекурсивних визначень, в визначенні деякого попереднього типу. Самі наочні приклади рекурсивних структур - це конструкції описів арифметичних та логічних виразів різноманітних мов програмування, де рекурсія відображає можливості вживання одного виразу в середині іншого.
Взагалі в результаті застосування вкладених структур даних можна обробляти скільки завгодно складних типів даних.
Добре знайомим прикладом рекурсивно визначених даних є генеологічне дерево (в ньому з кожною людиною зв'язується генеологічне дерево всіх його предків).
Приклад:
Function FIB (n: integer): integer;
Веgіn
If n<=1 then FIB:=l
Else FIB: =FIB(n-l)+FIB(n-2);
End;
Рекурсії мають дві найбільш важливі області застосування:
1. З теоретичної точки зору, рекурсивні визначення є основою всієї сучасної теорії обчислювальних функцій.
2. Друга область застосування обумовлюється тим, що процедури аналізу структур, що є рекурсивними, найбільш ефективні, коли вони самі рекурсивні. Ці процедури повинні в якійсь мірі відображати деякі особливості, які були б необов'язковими при відсутності рекурсії в структурі даних.
Існують деякі функції, які можна легко визначити рекурсивно, але які не можна визначити в термінах звичайних алгебраїчних виразів.
Наприклад,функція Аккермана. Вона визначається для цілих додатніх чисел і для нуля:
А(m,n)=if m=0 then n+1 else
If n=0 then A(m-1,1) else
А(m-1),А (m, n-1);
Об'єм пам'яті обмежує глибину рекурсії, але це не є суттєвим в задачах аналізу речень, де обмеження зв'язані з довжиною вхідних даних, але не з їх структурою.
Розглянемо функцію n!. Як правило її визначають як добуток перших n чисел
N!=1*2*3…n
Такий добуток можна легко обчислити за допомогою інтерактивних конструкцій, наприклад, оператора циклу for
Begin
read(n);
Fact:=1;
For i:=1 to n do
Fact:=fact*I;
Але існує іще одне визначення факторіалу, в якому використовується рекурентна формула, що має такий вигляд:
0!=1
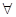n>0 n!=n*(n-1)!
Визначення за допомогою рекурентних формул іноді називають рекурсивними визначеннями. Програма, яка використовує рекурсивну функцію для обчислення факторіалу має такий вигляд:
Program f;
Var n:integer;
Function fact (i:integer):longint;
Begin
If i=1 then fact:=1
Else fact:=i*fact(i-1)
End;
Begin
Write(‘Введіть число n’);
Read(n);
Writeln(‘Факт n!= ‘,fact(n));
End.
Для створення рекурсивних алгоритмів необхідно і достатньо наявність поняття процедури чи функції. Це виходить з того, що процедури та функції дозволяють дати любим послідовним діям ім’я, за допомогою якого буде можливо цю послідовність дій викликати.
Програми, в яких використовуються рекурсивні підпрограми відрізняються простотою, наглядністю та компактністю тексту. Однак, при цьому неефективно використовується оперативна пам’ять (під локальні зміні весь час відводяться нові комірки пам’яті).
Головні умови до рекурсивних процедур заключаються в тому, що виклик рекурсивної процедури повинен виконуватися при умові, яка на якомусь рівні рекурсії стане хибною.
Структура рекурсивної процедури може приймати три різні форми:
1. Форма з виконанням дій до рекурсивного виклику.
Procedure A;
Begin
K;
If умова then A;
End;
2. Форма з виконанням дій після рекурсивного виклику.
Procedure А;
Begin
If умова then A;
K;
End;
3. Форма з виконанням дій як до так і після рекурсивного виклику.
Procedure A;
Begin
K1;
If умова then A;
K2;
End;
Багатьом задачам все рівно, яка використовується форма рекурсивної процедури. Однак, є задачі при рішенні яких програмісту потрібно керувати ходом роботи рекурсивних процедур та функцій. До таких задач відносяться задачі, які використовують спискові та деревовидні структури даних.
Прикладом складних рекурсивних зв’язків є задача про Ханойські башні.
А В С
Дано три стовпчики А,В,С. На стовпчик А один на другому знаходяться чотири диски різного діаметру, пронумеровані зверху вниз. Причому, вони розміщені так, що кожний менший знаходиться на більшому. Треба перемістити ці чотири диски на стовпчик С, зберігши їх взаємне розміщення. В використовують як допоміжний стовпчик. За один крок дозволяється перемістити один із верхніх дисків любого стовпчика, крім того більший диск ніколи не дозволяється класти на диск меншого діаметру.
Множини.
До складних типів даних крім масивів відносяться множини. В математиці під множиною розуміється деякий набір елементів. До множин застосовують наступні операції:
1. Об 'єднання двух множин : А=В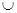
C
В цьому випадку кожний елемент множини А являється або елементом множини В, або елементом множини С.
2. Перетин двух множин : А=В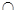
С
В цьому випадку кожний елемент множини А являється елементом множин В і С одночасно.
З. Різниця двух множин: А=В\С
В цьому випадку кожний елемент множини А являється елементом множини В, але не являється елементом множини С.
Приклади операцій над множинами:
1. (коло, ромб)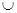(коло, квадрат)=(ромб, коло, квадрат)
2. (коло)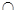(коло, ромб, квадрат)=(коло)
3. (коло, ромб, квадрат) \ (коло, квадрат)=(ромб)
Елементи множини не впорядковані, тому наступні записи (1,5,7,3) (3,5,7,1) (5,1,7,3) однакові.
Під множиною в Паскалі розуміють обмежений, невпорядкований набір елементів однакового типу. Всій множині в цілому дається ім'я. Тип елементів, що входять в множину, називається базовим. В якості базового типу можна використовувати прості типи: стандартні(крім дійсного), а також змінні: перелічувальні та граничні. Множини повинні бути об'явлені або в Var, або з використанням розділів типів Tуре.
Об'ява множини в розділі змінних Var має наступний вигляд:
Var ім'я_множ: Set of<базовий тип>;
Приклад: Var god: set of 1990.. 2000;
Об'ява множини в розділі опису типів type:
Туре ім'я_типу = set of<базовий тип>;
Var ім'я_множ: ім'я_типу;
Значення змінних і констант множини задаються в розділі операторів за допомогою конструктора.
Конструктор - це список елементів базового типу, взятих у квадратні дужки:
Приклад: ФИГУРА:=[РОМБ];
М:=['А', 'В', 'С'];
K:=[];
В Паскалі використовують наступні операції над множинами, за допомогою яких можна будувати різні вирази множинного типу:
1. + об'єднання;
2. * перетин;
3. - різниця;
4.=, <> перевірка множин на рівність.
(Множина А=В, якщо кожний елемент множини А являється елементом множини В і навпаки, у протилежному випадку множини А і В не рівні).
5. < =, > = перевірка множини на включення. (Множина А включена в множину В, якщо всі елементи множини А являються також елементами множини В).
6. IN— перевірка на належність елементу множині. (Ця операція служить для перевірки: чи належить елемент базового типу С множині А. Зліва від IN в загальному випадку пишеться вираз відповідного базового типу, а справа вираз множинного типу : 6 IN [5.. 8].
Так вираз: М+2 IN [1.. 7]*[4,6,8] при М=1 має значення false, так як 3 не входить в множину.
Операції, призначені для роботи з множинами розміщені так в порядку'
зменьшення:
1. *
2. +,-
3. IN, =, <>, <=, > =
Послідовність виконання операцій одного пріоритету визначається порядком їх появи у виразі. Для зміни порядку виконання використовують круглі дужки.
Додатково до вище розглянутих операцій можна використовувати ще дві ( версія 7.0):
7. INCLUDE (A,Х) – включає новий елемент у множину, де
А – множина, що складається з елементів базового типу.
Х – елемент базового типу.
8. EXCLUDE(A,X) – виключає елемент із множини.
Параметри ті ж самі, що і у процедурі INCLUDE.
Множини дозволяють скоротити програму та зробити її більш наглядною за рахунок зменьшення кількості різних перевірок.
Приклад: Які із приведених нижче виразів являються неправильними:
1. ['A’,’B',’C',’K']/['A',’B'] - неправильний (немає в Pascal такого оператора)
2. [7,2,8,4] =[2,4,7,8] - правильний
3. [куб,куля] + [призма] - правильний = [куб, куля, призма]
4. [5.3..8.0, 1.9]+[1.2] - неправильний - використовується дійсний тип даних
Обчислити вирази:
1. [7] <=[1..7]=true
2. ['A'.. 'F', 'K’.. 'N']+['F'.. 'K']=['A'.. 'N']
3.[Києв,Xарьків,Одеса]+[Одеса]=[Київ, Харьків, Одеса]
4.10 IN [1..7]=false
5. trunc(7.5) IN [1..9]=True
Для виведення елементів деякої множини, яку сформували в процесі виконання програми, необхідно скористатися оператором циклу, в середині якого була б перевірка на належність поточного значення параметру цикла наведеній множині. Наприклад, для множини АВ,описаної як var AB:set of 'A'.. 'Z';
можливо організувати виведення елементів таким чином
for І: = 'A' to 'Z' do
if I IN AB then write(I:2);
Причому, параметр циклу І повинен бути описаний як символьна зміна, або як
І: 'A'.. 'Z';
Друк елементів множини проводиться в тому порядку, в якому вони зустрічалися в базовій множині.
Дано:
Туре деньтижня=(пн,вв,ср,..,нед);
Описати множинний тип, який включає в себе множини із
а) назв любих днів тижня ( type A= set of деньтижня;)
б) назв робочих днів тижня ( type B=set of пн . . пт;)
Приклад: Є три множини символьного типу, які задані своїми конструкціями:
Y1=['A’,’B’,’D',’R',’M'];
у2=['R','А’,'Н','D’];
уЗ=['А',’R’];
Сформувати нову множину: x=(yl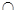y2)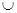(y1\y2) Вивести на друк отриману множину, перевірити чи входить множина уЗ в множину х..
program mnl;
var yl,y2,y3,x:set of char;
c:char;
begin
y1:=['a',’b',’d',’r',’m'];
y2:=[‘r’,’a’,’h’,’d’];
y3:=['a','r'];
{формуємо множину x}
x:=(yl*y2)+(yl-y2);
write ('множина х складаїться з ');
for c:='a' to ‘r’ do
if c in x then write (c:2);
{перевірка на входження множини у3 в множину х}
if y3 <= x then
writeln('множина уЗ входить в множину х');
else writeln('множина у3 не входить в множину х');
end.
Приклад: Є довільний текст. Визначити, які цифри є у тексті. Якщо цифр немає вивести повідомлення.
program mn2;
var nol,m:set of 0. .9;
c:char;
i,k: integer;
begin
writeln('Введіть текст');
nol:=[];
repeat
read(c);
k:=ord(c)-ord(‘0’);
if k in [0..9] then
nol: =nol+[k]
until c=’.’;
if nol=[] then
writeln('в тексті цифр немає')
else writeln ('в тексті є такі цифри');
for і: =1 to 9 do
if і in nol then write(i:2);
end.
(ORD – знаходження порядкового номера).
Приклад: type str=array[1..20] of char. Написати програму, яка підраховує загальну кількість знаків ‘+’,’-‘,’*’, що входять в рядок.
Program mn4;
Type str=array[1..20] of char;
Var c:str;
I,x:integer;
M:set of char;
Begin
M:=[‘+’,’-‘,’*’];
I:=1;
x:=0;
writeln(‘введіть рядок');
repeat
read(c[i]);
i:=i+1;
until eoln;
for i: =1 to 20 do
if c[і] in m then x:=x+1;
writelп('кількість знаків в рядку: ‘,x:2);
end.
Приклад: Дано 30 цілих чисел. Визначити, скільки серед цих чисел, числа які починаються на 1 або 2 у десятковому записі числа.
program mn5;
var chisla:set of 0..30;
kol, k, і:integer;
begin
kol:=0;
chisla:=[1,2,10..29];
writeln('введіть числа'); for і: =1 to 30 do
begin
read(k);
if k in chisla then kol: =kol+l;
end;
writeln('кількість чисел=',kol:2);
end.
Записи.
До складних типів даних відносяться і записи. В багатьох економічних та інформаційних задачах обробляються відомості, документи, каталоги та списки. При цьому виникає потреба об'єднувати дані різного типу в одну групу. Для роботи з групою даних в Паскалі введено поняття запису.
Запис являє собою сукупність обмеженого числа даних різного типу. Розглянемо відомість списку студентів з їх оцінками:
Кожний рядок в цій відомості складається з окремих елементів - даних різного типу, де порядковий номер - це ціле десяткове число, ПІБ - масив символів, Оцінки - масив цілих чисел. Всі ці дані можна об'єднати в одну групу і вважати записом. Запис в цілому і окремі його елементи позначаються іменами. Позначимо:
В - ім'я всього запису;
N - порядковий номер;
FIO - ПІБ;
Ok - оцінки.
Звернення до елементів запису у програмі виконується за допомогою уточненого складеного імені. Уточнене ім'я містить ім'я запису та ім'я елементу і записується:
B.N або B.FIO. Записи як і інші дані об'являються в розділі опису. Об'яву запису можна робити у розділі опису var або у розділі опису типів:
Var ім'я_запису: RECORD
Ім'я1:тип;
Ім'я2: тип;
