#include <conio.h>
#include <iostream.h>
#include "matrix.h"
typedef matrix<double> dmatrix;
typedef vector<double> dvector;
//Определим некоторые вспомогательные подпрограммы
//Возвращает код знака числа
inline long sign(double x)
{
return (x>0)?1:((x<0)?-1:0);
}
/*Простой параболоид для тестирования многомерного поиска*/
double gv(dvector x)
{
double sum=0;
int i;
int r=x.getm();
for(i=0;i<r;i++)
sum+=10.0*(x[i]-4)*(x[i]-4);
return sum;
}
/*Простейшая функция для численного дифференцирования, возвращающая значение вектора градиента в заданной точке при заданной матрице ограничений на составляющие аргумента*/
dvector GetGrad(dvector x, dmatrix rm)
{
int r=x.getm();
dvector grad(r);
double _yold=gv(x), //Текущее значение функции
_ynew, dx;
for(int i=0;i<r;i++)
{
/*Приращение аргумента возьмем в малую долю его интервала*/
dx=fabs(rm[i][1]-rm[i][0])*1e-10;
x[i]+=dx;
_ynew=(gv(x)); //Новое значение функции
/*Составляющая вектора градиента*/
grad[i]=(_ynew-_yold)/(dx);
x[i]-=dx;
}
return (~grad);//Возвращаем, нормировав по модулю
}
/*Функциональный класс объектов для многомерного поиска экстремума*/
class MultiExtremum
{
/*Размерность вектора аргументов исследуемой функции*/
long range;
/*матрица ограничений на значения составляющих вектора аргументов*/
dmatrix rm;
dvector veps;/*Вектор допустимых погрешностей по аргументу*/
/*Указатель на подпрограмму, возвращающую значение исследуемой функции при заданном векторе ее аргументов*/
double (*getv)(dvector x);
public:
/*Конструктор для многомерного поиска примет аргументы - мерность пространства, матрицу ограничений, вектор допустимых погрешностей, указатель на подпрограмму вычисления значений функции*/
MultiExtremum(long RANGE, dmatrix RM, dvector VEPS, double (*GETV)(dvector XM)): range(RANGE), rm(RM), veps(VEPS), getv(GETV) {}
/*Прототипы функций решения задачи условной оптимизации*/
void MultiDihot(dvector& x,int n); /*вспомогательный метод дихотомии*/
dvector Coord(); //метод покоординатного спуска
dvector Grad(); //метод градиента
dvector PSM(); //последовательный симплекс-метод
};
/*Реализация локального поиска экстремума по одной координате методом дихотомии*/
void MultiExtremum::MultiDihot(dvector& x,int n)
{
double xl,xr,yl,yr,dt=rm[n][1],ct=rm[n][0];
for(;(dt-ct)>veps[n];)
{
x[n]=xl=(ct+dt)/2-0.01*fabs(dt-ct);
yl=getv(x);
x[n]=xr=(ct+dt)/2+0.01*fabs(dt-ct);
yr=getv(x);
if(sign(yl-yr)>0)
{
ct=xl;
xl=xr;
xr=ct+dt-xl;
}
else
{
dt=xr;
xr=xl;
xl=ct+dt-xr;
}
}
x[n]=(ct+dt)/2;
}
//Методы многомерного поиска
//Координатный спуск
dvector MultiExtremum ::Coord()
{
dvector xtp(range),xtn(range), xeps(range);
int i,flag;
for(i=0;i<range;i++)
xtp[i]=xtn[i]=0.5*(rm[i][0]+rm[i][1]);
for(;;)
{
flag=0;
for(i=0;i<range;i++)
MultiDihot(xtn,i);
xeps=xtn-xtp;
for(i=0;i<range;i++)
if(fabs(xeps[i])>fabs(veps[i]))
flag++;
if(!flag)
break;
else
xtp=xtn;
}
return xtn;
}
//Метод градиента
dvector MultiExtremum::Grad()
{
double k=5.0,vn,vp;
dvector xtp(range), xtn(range), xeps(range), gr(range);
/*Вначале станем в средину допустимой области поиска*/
for(int i=0;i<range;i++)
xtp[i]=(0.5*(rm[i][0]+rm[i][1]));
for(;;)
{
//Вычислим градиент
gr=GetGrad(xtp,rm);
/*Корректируем аргумент в направлении, противоположном градиенту*/
xtn=xtp-k*gr;
vn=getv(xtn);
vp=getv(xtp);
//Если шаг слишком большой - уменьшаем его
for(;vn>vp;)
{
k/=1.2;
xtn=xtp-k*gr;
vn=getv(xtn);
vp=getv(xtp);
}
/*Если шаг по градиенту не изменяет существенно значение функции - прекращаем поиск*/
if(fabs(getv(xtn)-getv(xtp))<1e-8)
break;
xtp=xtn;
}
return xtn;
}
/*Последовательный симплекс-метод.
Этот метод достаточно громоздок в программном исполнении, особенно при использовании переменного размера поискового симплекса, защиты от вращения симплекса вокруг одной из вершин и других манипуляций, необходимых для его эффективной работы. Мы приводим упрощенный, а, следовательно, не очень точный в вычислениях пример программы, демонстрирующий принцип работы алгоритма */
dvector MultiExtremum::PSM()
{
double sum;
int i,j;
dvector yv(range+1);/*Вектор значений функции в вершинах симплекса*/
/*Формируем исходный регулярный симплекс в пространстве размерности range с центром в начале координат */
dmatrix simp(range+1,range);/*матрица для вершин симплекса*/
dvector stmp(range);
const double L=2.0L;
//заполняем матрицу симплекса
//Сначала нулевую строку
for(j=0;j<range;j++)
simp[0][j]=0.0;
//Затем остальные
double pk=(L/(range*sqrt(2)))*
(sqrt(range+1)+double(range)-1.0);
double qk=L*(pk-0.5*sqrt(2));
for(i=1;i<(range+1);i++)
for(j=0;j<range;j++)
simp[i][j]=(j==(i-1))?pk:qk;
int pmax=-1,//предыдущая плохая
cicl;
int vmin=0,vmax=0;
//Бесконечный цикл поиска
for(cicl=1;/*cicl<100000*/;cicl++)
{
//Вычисляем значения функции во всех вершинах
for(i=0;i<(range+1);i++)
yv[i]=getv(simp[i]);
/*Отыскиваем номера наихудшей и наилучшей вершин*/
for(i=1;i<(range+1);i++)
{
if(yv[i]>yv[vmax])
vmax=i;
if(yv[i]<yv[vmin])
vmin=i;
}
/*Если наилучшая нас устраивает - прекращаем поиск*/
if(fabs(yv[vmin])<0.05)
break;/*Грубая оценка попадания в зону экстремума. В этом месте вместо break можно было бы уменьшить размер симплекса и условие достижения экстремума*/
/*Если плохая не сменила номер - ищем ближайшую плохую*/
if((cicl>1)&&(vmax==pmax))
for(i=1;i<(range+1);i++)
{
if((yv[i]>yv[vmax])&&(i!=pmax))
vmax=i;
}
pmax=vmax;//Запоминаем как предыдущую плохую
//меняем плохую вершину на зеркально отраженную
for(j=0;j<range;j++)//j-номер координаты
{
/*Для каждой координаты вычислим ее среднее значение по всем вершинам*/
sum=0;
for(int k=0;k<(range+1);k++)
sum+=simp[k][j];//k- номер вершины
sum*=(2.0/(range+1));
/*Из среднего вычитаем плохое значение и результат сохраняем в промежуточном векторе*/
stmp[j]=sum-simp[vmax][j];
}
/*Новый вектор координат переносим на место наихудшей вершины*/
simp[vmax]=stmp;
}//бесконечный цикл
return simp[vmin];
}
//Программа тестирования методов поиска экстремума
main()
{
//Тестируем многомерные методы поиска экстремума
/*Формируем размерность, матрицу ограничений и вектор погрешностей*/
int r=5;
dmatrix m(r,2);dvector e(R);
for(int i=0;i<r;i++)
{
m[i][0]=-8.0;
m[i][1]=15.0;
e[i]=0.0001;
}
MultiExtremum extM(r,m,e,gv);/*Конструируем объект*/
/*Вызываем для этого объекта методы поиска минимума*/
dvector resCoord=extM.Coord(); /*Метод покоординатного спуска*/
cout<<endl<<gv(resCoord);
cout<<endl<<resCoord;
dvector resGrad=extM.Grad(); /*Метод градиента (наискорейшего спуска)*/
cout<<endl<<gv(resGrad);
cout<<endl<<resGrad;
dvector resPSM=extM.PSM(); /*Последовательный симплекс-метод*/
cout<<endl<<gv(resPSM);
cout<<endl<<resPSM;
getch();
}
Приложение. Как переносить данные в Ехсеl и отображать графики зависимостей
Пусть Вам необходимо отобразить в виде графика данные, которые находятся в файле. Вначале Вам необходимо скопировать эти данные в буфер обмена, используя, к примеру, Far. Для этого выберите режим редактирования файла, нажав клавишу F4 на имени файла, выделите необходимые Вам данные клавишами управления курсором (с прижатой Shift), нажатием Ctrl+Ins скопируйте помеченный блок в буфер обмена. Далее определите, какой вид у этих данных:
1. одна строка произвольной длины
2. один столбец произвольной длины
3. два столбца произвольной длины, первый из которых содержит независимую переменную, а второй – зависимую.
4. две строки произвольной длины, первая из которых содержит независимую переменную, а вторая – зависимую.
5. две строки длины до 64 чисел каждая, первая из которых содержит независимую переменную, а вторая – зависимую.
Случаи большего числа строк (столбцов) сводятся к этим пяти.
Запустите редактор Word и комбинацией Shift+Ins вставьте содержимое буфера обмена. Произведите замену точек на запятые: нажатием Ctrl+H вызовите диалоговое окно Найти и заменить, в поле Найти ввести точку, в поле Заменить на – запятую и нажать на клавишу Заменить все.
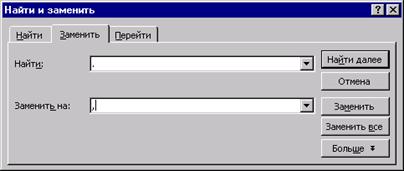
Рассмотрим возможные случаи:
1. Этот случай сводится ко второму заменой пробелов на символы абзаца:
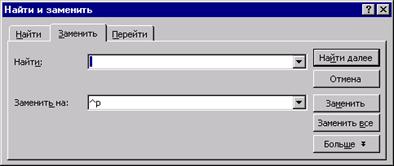
3, 5. Комбинацией Ctrl+А выделите весь текст в окне. Затем в пункте меню Таблица выберите пункт Преобразовать в таблицу.
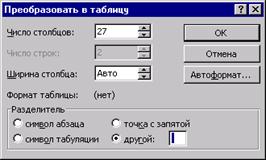
В появившемся диалоговом окне в качестве символа разделителя введите пробел (поле другой) и нажмите на клавишу ОК.
4. А не транспонировать ли Вам данные перед выводом в файл? Сводится к случаю 3.
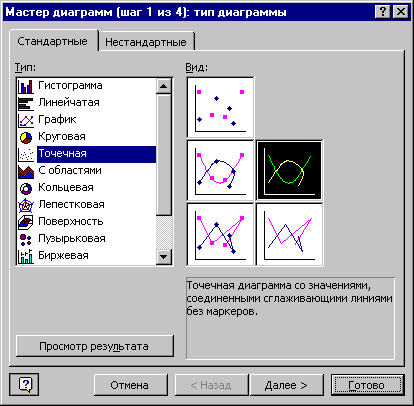
Следующий этап – выделение всего содержимого окна (Ctrl+А) и копирование выделенного фрагмента в буфер обмена (Ctrl+Ins), затем – запуск табличного процессора Excel и вставка содержимого буфера обмена нажатием Shift+Ins. Не снимая пометки, выберите пункт меню Вставка, а в нём – подпункт Диаграмма:
1, 2. В списке Тип выберите пункт График, а в разделе Вид – первый из предложенных видов графиков и нажмите на кнопку Готово.
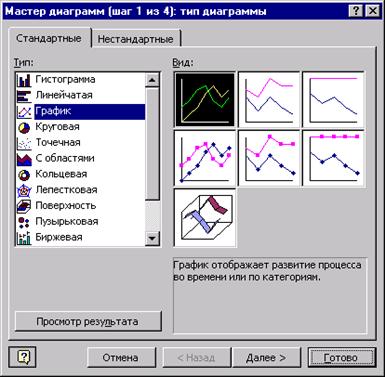
3, 4, 5. В списке Тип выберите пункт Точечная, а в разделе Вид – третий из предлагаемых видов графиков и нажмите на кнопку Готово.
Литература
1. Алгоритмы и программы восстановления зависимостей. – М.: Наука, 1984.
2. Анго А. Математика для электро- и радиоинженеров. – М.: Наука, 1964.
3. Бабак В.П., Хандецький В.С., Шрюфер Е. Обробка сигналів. – К.: Либідь, 1996.
4. Боглаев Ю.П. Вычислительная математика и программирование: Учебное пособие для студентов втузов. – М.: Высшая школа, 1990.
5. Вайнер Р., Пинсон Л. С++ изнутри. – Киев: ДиаСофт, 1993.
6. Вентцель Д.А., Вентцель Е.С. Элементы теории приближенных вычислений. – М.: Издательство ВВИА им. Н.Е. Жуковского, 1949.
7. Вентцель Е.С. Исследование операций. – М.: Радио и связь, 1970.
8. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969.
9. Гавурин М.К. Лекции по методам вычислений. – М.: Наука, 1971.
10. Гантмахер Ф.Р. Теория матриц. – М.: Государственное издательство технико-теоретической литературы, 1953.
11. Гринчишин Я.Т., Ефимов В.И., Ломакович А.Н. Алгоритмы и программы на Бейсике. – М.: Просвещение, 1988.
12. Гринчишин Я.Т. TURBO PASCAL: Чисельні методи в фізиці та математиці: Навч. посібник – Тернопіль, 1994.
13. Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 2: Пер. с англ. – М.: Мир, 1990.
14. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. – М.: Наука, 1970.
15. Дамбраускас А.П. Симплексный поиск. – М.: Энергия, 1979.
16. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Физматгиз, 1963.
17. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – М.: Наука, 1967.
18. Джордж А., Лю Дж. Численное решение больших разряжённых систем уравнений. – М.: Мир, 1984.
19. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. – М.: Наука, 1987.
20. Иванов В. В. Методы вычислений на ЭВМ: Справочное пособие. – К.: Наукова думка, 1986.
21. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М. Наука, 1973.
22. Лукас П. С++ под рукой. – Киев: ДиаСофт, 1993.
23. Лукомский Я.И. Теория корреляции и её применение к анализу производства. – М.: Госстатиздат ЦСУ СССР, 1961.
24. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977.
25. Маликов В.Т., Кветный Р.Н. Вычислительные методы и применение ЭВМ: Учебное пособие. – К.: Выща школа, 1989.
26. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: Раско, 1991.
27. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986.
28. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М.: Высшая школа, 1983.
29. Полищук А.П. Персональный компьютер и его программирование (С, С++, Паскаль). Учебно-справочное пособие. – Кривой Рог: КГПИ, 1997.
30. Попов В.С., Мансуров Н.Н., Николаев С.А. Электротехника. – М.: Издательство Министерства коммунального хозяйства РСФСР, 1958.
31. Смирнов В.И. Курс высшей математики. Т. 1-5. – М.: Наука, 1974.
32. Статистическая обработка результатов экспериментов на микро-ЭВМ и программируемых калькуляторах. – Л.: Энергоатомиздат, 1991.
33. Страуструп Б. Язык программирования С++: В 2-х частях. – К.: Диасофт, 1993.
34. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Учебное пособие для вузов. – М.: Наука, 1986.
35. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.-Л.: Государственное издательство технико-теоретической литературы, 1951.
36. Уилкинсон Дж., Райнш К. Справочник алгоритмов на языке Алгол. Линейная алебра. – М.: Машиностроение, 1976.
37. Уткіна С.В., Наришкіна Л.С. Алгебра і числові системи: Навч. посібник. – К.: Вища школа, 1995.
38. Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.: Гостехиздат, 1950.
39. Фейсон Т. Объектно-ориентированное программирование на Borland C++ 4.5. – Киев: Диалектика, 1996.
40. Форсайт Д., Малькольм М., Моллер К. Машинные методы математических вычислений. – М.: Мир, 1980.
41. Форсайт Д., Моллер К. Численное решение систем линейных алгебраических уравнений. – М.: Мир, 1968.
42. Хемминг Р.В. Численные методы. – М.: Наука, 1968.
43. Шуп Т.Е. Прикладные численные методы в физике и технике. – М.: Высшая школа, 1990.
44. Шуп Т.Е. Решение инженерных задач на ЭВМ. Практическое руководство. – М.: Мир, 1982.
Учебное пособие
Александр Павлович Полищук
Сергей Алексеевич Семериков
Методы вычислений в классах языка С++
| Подп. к печати 28.12.98
Бумага офсетная №1
Усл. кр.-от. 18,38
Тираж 500
| Формат 80х84 1/16.
Усл. печ. л. 18,38
Уч.-изд. л. 22,29
Зак. №12-2483
|
КГПИ, 324086, Кривой Рог-86, пр. Гагарина, 54
Криворожская городская типография
324050, Кривой Рог-50, пр. Металлургов, 28.






