Отже, гроші, що використовуються протягом періоду часу, мають приносити прибуток, який залежить від тривалості цього періоду. Цей прибуток виміряють у процентах від суми грошей, що використовується.
Проценти (від лат. per cent – на сотню) – сума доходу від надання капіталу в борг або плата за тимчасове користування капіталом в різних формах.
Процентна ставка – питомий показник, виражений у відсотках або коефіцієнтах, у відповідності з котрим в установлений термін нараховується сума відсотків на одиницю капіталу.
Практикуються два способи нарахування відсотків, в залежності від бази нарахування:
· прості проценти, коли відсотки нараховуються від початкової суми, здійснюється за формулою:
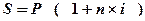 ,
,
де S– нарощена сума,
Р– сума, що вкладається,
і– відсоткова ставка.
n – кількість інтервалів нарахування процентів у загальному періоді інвестиції (наприклад, якщо здійснюється депозитний вклад терміном на п’ять років з щорічним нарахуванням відсотків, n =5, з нарахуванням відсотків кожного півріччя, то n =10);
Приклад
Початкова сума 100 грн., відсоткова ставка – 10% (простих), тоді нарощена сума дорівнює:
o наприкінці першого року: S1=100+100´0,1= 110грн.,
o наприкінці другого року: S2=110+100´0,1= 120грн. і т.д.
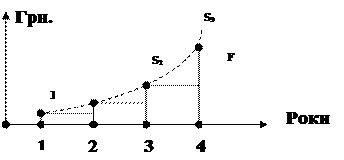
Тобто суми S1,S2,…,Sn являють собою арифметичну прогресію, яка графічно представлена на малюнку 3.
Рисунок 2. Нарощування суми S при простих відсотках
Прості відсотки найчастіше використовують для внутрішньорічних відрізків часу. Тоді nрозглядається як доля року:
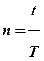 ,
,
де t– відрізок часу, до якого обчислюється сума (менший за 1 рік)
Т – тривалість року.
Нарощена сума Sв даному випадку обчислюється наступним чином:
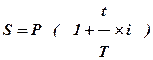
При цьому tможе вимірюватись двома способами:
§ точно – визначається точна кількість днів кредитування з використанням спеціальної таблиці, де вказані порядкові номери кожного дня року (із номеру до закінчення терміну кредитування віднімають номер першого дня;
§ приблизно – визначається приблизна кількість днів кредитування, при цьому полагають, що кожен місяць дорівнює 30 дням.
Для визначення Т також використовують два способи:
§ Точний – коли Т=365 (366) днів, тобто точна кількість днів у році. Такі відсотки називають точні відсотки;
§ Приблизний – коли вважають, що Т=360 днів (12 місяців по 30 днів) – звичайні або комерційні відсотки.
При цьому на практиці використовують три варіанти обчислення простих відсотків:
1. Точні відсотки з точною кількістю днів кредитування – обозначаються як 365/365 або АСТ/АСТ;
2. Звичайні відсотки з точною кількістю днів кредитування – обозначаються як 365/360 або АСТ/360;
3. Звичайні відсотки з приблизною кількістю днів кредитування – обозначаються як 365/360.
· складні проценти –відсотки нараховуються від нарощеної суми, тобто початкової суми, збільшеної на суму нарахованих відсотків:
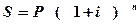
Приклад
Початкова сума 100 грн., відсоткова ставка – 10% (складних), тоді нарощена сума дорівнює:
o наприкінці першого року: S1=100+100´0,1= 110грн.,
o наприкінці другого року: S2=110+110´0,1= 121грн. і т.д.
Тобто суми S1,S2,…,Sn являють собою геометричну прогресію, яка графічно представлена на малюнку 4.
Рисунок 3. Нарощування суми S при складних відсотках
За способом нарахування розрізняють такі процентні ставки:
· Ставки нарощування (декурсивні ставки), коли відсотки нараховуються наприкінці кожного інтервалу та додаються до початкової суми вкладу або боргу.
Приклад
Початкова сума 100 грн., сума відсотків – 10грн (простих), тоді декурсивна процентна ставка дорівнює 10/100=0,1 або 10%.
· Ставки дисконтування або облікові ставки (антисипативні). Такі ставки використовують у вексельних, або в інших кредитних операціях. В даному разі відсотки нараховуються на початку кожного періоду та віднімаються з кінцевої суму боргу, тобто суми, що вказана на векселі.
Приклад
Яку суму необхідно надати в кредит (Р), якщо дисконтна ставка 20%, а повернути необхідно 200грн.?
Р=200-200´20%=160грн.
Теперішня вартість грошей при використанні облікової ставки обчислюється таким чином:
 , де
, де
Р – теперішня вартість грошей (дисконтова на сума боргу);
n – кількість періодів дисконтування (термін кредиту)
d – проста облікова ставка, або:
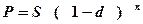 , де
, де
d – складна облікова ставка.
Період нарахування – загальний проміжок часу, за який нарощуються або дисконтуються відсотки, тобто загальний термін нарахування відсотків.
Інтервал нарахування – мінімальний часовий термін (в межах загального періоду нарахування) по закінченню якого нараховуються відсотки.
Приклад
Кредит надається терміном на 1 рік (період нарахування), з щомісячним нарахуванням відсотків (інтервал нарахування).
Майбутня вартість грошей – сума інвестуємих в теперішній час грошей, збільшена за відповідної процентною ставкою через певний проміжок часу, тобто нарощена сума.
Теперішня вартість грошей – сума, що вкладається, або кінцева сума боргу приведена з врахуванням відповідної відсоткової ставки к нинішньому часовому періоду, тобто дисконтова на сума.
Нарощення вартості (компаудінг) – збільшення суми інвестуємих в даний час грошових коштів на суму нарахованих відсотків (приведення теперішньої вартості грошей до їх майбутньої вартості).
Дисконтування вартості – зменшення майбутньої суми грошей за рахунок віднімання суми дисконту (приведення майбутньої вартості грошей до їх теперішньої вартості).


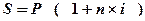 ,
,
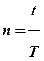 ,
,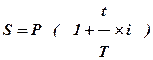
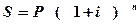
 , де
, де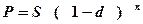 , де
, де