Як ми вже відзначали, математичним образом детермінованого хаотичного режиму в динамічній системі є дивні аттрактори, які мають надзвичайно складну геометричну структуру. Однією з важливих характеристик будь-якого геометричного об'єкту є його розмірність. На даний час розглядається багато типів розмірностей для аттракторів динамічних систем. Наприклад, фрактальна ємкість, розмірність Хаусдорфа-Безіковича, інформаційна і кореляційна розмірності, узагальнені розмірності Рені і так далі. Такі розмірності можуть давати істотну інформацію про структуру аттрактора, служити кількісною відміною ознакою регулярного аттрактора від дивних, а для дивних аттракторов виступати як якась міра «дивацтва» аттрактора.
Практично всі відомі дивні аттрактори є фрактальною множиною, яка має дробову розмірність Хаусдорфа- Безіковича. Цим вони відрізняються від регулярних аттракторов, відповідна розмірність яких є цілою. Безпосередній підрахунок фрактальної розмірності дивного аттрактора є надзвичайно трудомістким завданням, для вирішення якої в загальному випадку не існує яких-небудь стандартних алгоритмів. Проте порівняно просто може бути підрахована так звана ляпуновская розмірність аттрактора, яка на практиці найчастіше використовується як кількісна міра фрактальності.
Розгледимо диссипативну динамічну систему розмірності п. Поряд з початковою динамічною системою розглянемо ансамбль її ідентичних копій, які відрізняються одна від одної тільки різними початковими станами. У початковий момент часу у фазовому просторі цьому ансамблю відповідатиме якась «хмара» точок, що зображаються. В процесі еволюції початкова хмара змінюватиметься відповідно до динаміки системи, що задається її математичною моделлю.
Передбачимо, що біля даної динамічної системи існує дивний аттрактор. Спектр ЛХП такого аттрактора складається з п показників, впорядкованих по убуванню 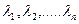 . Причому
. Причому 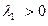 і принаймні, існує один нульовий показник. Крім того, в силу диссипативності системи, сумма всіх ляпуновских характеристичних показників негативна:
і принаймні, існує один нульовий показник. Крім того, в силу диссипативності системи, сумма всіх ляпуновских характеристичних показників негативна:
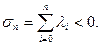 (2.7)
(2.7)
Будемо послідовно обчислювати суми вигляду (2.7) для m=1,2,…Спочатку ми будемо отримувати додатні, а потім від’ємні величини 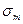 .Знайдемо таке m, що
.Знайдемо таке m, що  , але
, але  . В суму
. В суму 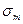 увійдуть всі додатні, всі нульові і частина від’ємних ляпуновських характеристичних показників. Якщо розглядати підпростір,що створений векторами збурень, які відповідають першим m ляпуновським показникам, то в цьому підпросторі об’єм “хмари” зображаючих точок асамбля систем не зменшиться в процесі еволюції, зокрема, зростає при
увійдуть всі додатні, всі нульові і частина від’ємних ляпуновських характеристичних показників. Якщо розглядати підпростір,що створений векторами збурень, які відповідають першим m ляпуновським показникам, то в цьому підпросторі об’єм “хмари” зображаючих точок асамбля систем не зменшиться в процесі еволюції, зокрема, зростає при 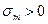 . В той же час в підпросторі, що сторений векторами збурень, які відповідають першим m+1 характеристичним показникам, об’єм “хмари” зображаючих точок буде зменшуватися при збільшені часу.
. В той же час в підпросторі, що сторений векторами збурень, які відповідають першим m+1 характеристичним показникам, об’єм “хмари” зображаючих точок буде зменшуватися при збільшені часу.
В 1979 році Каплан і Йорк запропонували гіпотузу, сенс якої полягає в тому, що фрактальна розмірність аттрактору  розташована в інтервалі
розташована в інтервалі
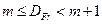
І складається із цілої m та деякої дробової частини d так, що
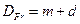
Причому ця дробова розмірність визначається із умови, що рух на аттракторі відповідає фізичним представленням про стаціонарність процесу, а саме:
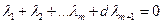
Звідси отримуємо, що розмірність аттрактору  визначається за формулою:
визначається за формулою:

Ця формула називається формулою Каплана-Йорка.
7. Методи та критерії виявлення хаосу в нелінійних системах за спостереженнями певної точки х в n-вимірному просторі за рівні проміжки часу: алгоритм Вольфа та Херста.
Методика дослідження нелінійної динаміки в економічних системах та процесах представляє собою 2 підходи. Перший – теоретичний. Тобто сюди можна віднести спроби на основі базових моделей теорії хаосу побудувати узагальнену модель, що враховує усі особливості функціонування економічної системи або процесу; розробку та теоретичне обґрунтування нових моделей, тестів критеріїв; побудова специфікацій моделей на основі обраної економічної теорії з наступним аналізом. Другий – експериментальний підхід. Метою його є побудова моделі прогнозування для отримання короткострокового чи довгострокового прогнозу без заданої математичної моделі, а лише за даними спостережень – часового ряду.
Формальним критерієм перевірки регресії на лінійність є:

1.BDS-тест.
Це варіант кореляційної розмірності, що в основному вимірює статистичну значимість обчисленої кореляційної розмірності. Він дозволяє відрізнити випадкові системи від детермінованого хаосу чи від нелінійних стохастичних систем. Одначе, він не може відрізнити нелінійну детерміновану систему і нелінійну стохастичну систему. BDS-статистика w є нормально розподіленою: 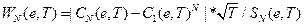 , де
, де
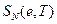 - стандартне відхилення кореляційних інтегралів;
- стандартне відхилення кореляційних інтегралів;
Т – число спостережень; Е- відстань; N – фазова розмірність;
СN – кореляційний інтеграл розмірності N.
Коли BDS-статистика w більша 2.0, то можна з 95% впевненістю відхилити нульову гіпотезу, згідно якої система, що вивчається, є випадковою. Якщо w більше 3.0, то ми можемо відхилити цю теорію з 99% впевненістю. Але BDS-тест знайде лінійну, так же як і нелінійну залежність в даних. Тому для цього дослідження необхідно взяти AR(1)-різниці. Крім того, подібно до R\S-аналізу,залежність може бути стохастичною (як процес Херста чи GARCH), чи вона може бути детермінованою (як хаос).
2.Проведення тесту залишків Брока.
Цей тест ґрунтується на чудовій властивості хаотичних часових рядів – інваріантності до лінійних перетворень. Якщо провести лінійне перетворення хаотичних даних, тоді обидва: і вихідний і трансформований ряди будуть мати одну і ту ж саму кореляційну розмірність та однакові показники Ляпунова. Якщо обчислені оцінки кореляційної розмірності і показників Ляпунова для перетвореного ряду істотно відрізняються, тоді гіпотеза про детермінований хаос відхиляється.
3.Проведення тасуючої діагностики.
Якщо ряд не містить якої-небудь нелінійної структури та породжується випадковим процесом, тоді тасування ряду шляхом вибору та переміщення його елементів створить новий ряд з оцінкою розмірності, аналогічній оцінці для вихідного ряду. Якщо, однак, ряд містить нелінійну структуру, процес тасування порушить її. У цьому випадку оцінка кореляційної розмірності тасованого ряду буде значно більше ніж оцінка розмірності вихідного ряду.
4.Графічний тест Гілмора.
Графічний тест хаосу, запропонований Гілмором, виявляє нестійкі періодичні орбіти, укладені в дивному аттракторі. Для того, щоб виявити ці області ”тісного повернення” у множині даних, потрібно побудувати спеціальним чином розфарбований графік. Обчислюються всі різниці 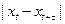 . Якщо різниця менше, ніж
. Якщо різниця менше, ніж 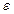 , то це позначається на графіку чорними кольорами, якщо більше, ніж
, то це позначається на графіку чорними кольорами, якщо більше, ніж 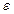 , то це позначається білим кольором.
, то це позначається білим кольором.
5.К-ентропія Колмогорова.
Значення її визначається в такий спосіб:

Якщо 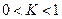 , то можна припустити наявність детермінованого хаосу в поводженні системи.
, то можна припустити наявність детермінованого хаосу в поводженні системи.
6.Визначення показника Херста.
7.Знаходження найбільшого показника Ляпунова, який характеризує чи є чутлива залежність від початкових умов та чи присутній в системі дивний аттрактор.
Розглянемо докладніше алгоритм Вольфа та Херста.


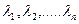 . Причому
. Причому 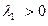 і принаймні, існує один нульовий показник. Крім того, в силу диссипативності системи, сумма всіх ляпуновских характеристичних показників негативна:
і принаймні, існує один нульовий показник. Крім того, в силу диссипативності системи, сумма всіх ляпуновских характеристичних показників негативна: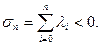 (2.7)
(2.7)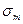 .Знайдемо таке m, що
.Знайдемо таке m, що  , але
, але  . В суму
. В суму 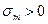 . В той же час в підпросторі, що сторений векторами збурень, які відповідають першим m+1 характеристичним показникам, об’єм “хмари” зображаючих точок буде зменшуватися при збільшені часу.
. В той же час в підпросторі, що сторений векторами збурень, які відповідають першим m+1 характеристичним показникам, об’єм “хмари” зображаючих точок буде зменшуватися при збільшені часу. розташована в інтервалі
розташована в інтервалі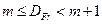
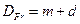
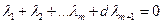


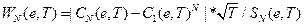 , де
, де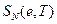 - стандартне відхилення кореляційних інтегралів;
- стандартне відхилення кореляційних інтегралів;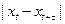 . Якщо різниця менше, ніж
. Якщо різниця менше, ніж 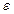 , то це позначається на графіку чорними кольорами, якщо більше, ніж
, то це позначається на графіку чорними кольорами, якщо більше, ніж 
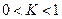 , то можна припустити наявність детермінованого хаосу в поводженні системи.
, то можна припустити наявність детермінованого хаосу в поводженні системи.