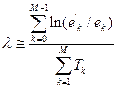Алгоритм Вольфа - найбільш часто використовуваний на практиці метод розрахунку показників Ляпунова по тимчасовому ряду, запропонований в статті Вольфа із співавторами (Physica D, 1984). Цей метод трохи нагадує стандартний підхід до обчислення спектру показників Ляпунова систем по відомій математичній моделі (метод Бенеттіна). Ми не можемо розрахувати повний спектр показників Ляпунова, оскільки нам невідомі рівняння руху. Проте Волфом був розроблений метод для розрахунку найбільшого показника Ляпунова 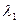 за експериментальними даними. Показник
за експериментальними даними. Показник 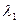 більший 0, свідчить про те, що є чутлива залежність від початкових умов і що в системі існує дивний аттрактор. За допомогою цього методу вимірюється розбігання довколишніх точок у відновленому фазовому просторі і указується як змінюється швидкість розбігання за межами фіксованих інтервалів часу.
більший 0, свідчить про те, що є чутлива залежність від початкових умов і що в системі існує дивний аттрактор. За допомогою цього методу вимірюється розбігання довколишніх точок у відновленому фазовому просторі і указується як змінюється швидкість розбігання за межами фіксованих інтервалів часу.
Спочатку вибираються дві точки, віддалені одна від одної принаймні на один орбітальний період. Після встановленого інтервалу часу («еволюційного періоду») вимірюється відстань між цими двома точками. Якщо відстань стає дуже великиою, шукається точка заміни тією ж кутовою орієнтацією руху, що і у початкової точки. Відносна кутова орієнтація нової пари точок повинна бути по можливості ближче до орієнтації пари початкової.
Точка заміни є необхідною, оскільки ми вимірюємо тільки розтягування, або розбігання у фазовому просторі. Якщо ці точки віддалені далеко, вони складуться одна на одну, що буде мірою конвергенції. Конвергенція не є частиною 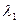 . На мал. 9 схематично представлений цей алгоритм. Формально він записується таким чином:
. На мал. 9 схематично представлений цей алгоритм. Формально він записується таким чином:

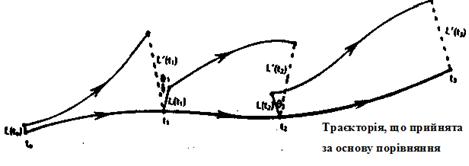
Мал.9. Схематичне представлення алгоритма Вольфа для оцінки найбільшого показника Ляпунова за часовим рядом.
Теоретично при нескінченній кількості незашумленшых даних рівняння  еквівалентне рівнянню
еквівалентне рівнянню 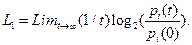 У реальності ми повинні мати справу з обмеженою кількістю зашумленных даних — це означає, що розмірність вкладення, часовий лаг і допустимі максимальне і мінімальні дистанції між точками повинні вибиратися з обачністю.
У реальності ми повинні мати справу з обмеженою кількістю зашумленных даних — це означає, що розмірність вкладення, часовий лаг і допустимі максимальне і мінімальні дистанції між точками повинні вибиратися з обачністю.
На щастя, Вольф дав декілька «правил великого пальця» для обробки експериментальних даних. По-перше розмірність вкладення повинна бути більш ніж у фазовогого простору аттрактора. Вольф із співавторами встановили, що еволюція довжини не повинна перевищувати 10% довжин аттрактора у фазовому просторі. По суті максимальна довжина не повинна перевищувати 10% різниць між максимальною і мінімальною величинами тимчасового ряду. Вольф із співавторами пришли до цього числа експериментально, оскільки логіка, що стоїть за цими міркуваннями, мабуть, не піддається точному кількісному аналізу. Тимчасова еволюція повинна бути достатньо довгою для того, щоб зміряти розтягування, але не складання. І тут немає правила — просто чим коротше, тим краще. Тут повинен бути дотриманий компроміс: хоча короткі періоди еволюції вимагають більше обчислень, при цьому має місце менше точкових замін, і в результаті збіжність стійкіша.
Після завершення обчислень по довгому тимчасовому ряду виходить стійка величина 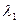 . Якщо немає стійкої збіжності, це означає, що параметри вибрані невірно, або бракує циклів даних для аналізу, або система насправді не є нелінійною.
. Якщо немає стійкої збіжності, це означає, що параметри вибрані невірно, або бракує циклів даних для аналізу, або система насправді не є нелінійною.
Вимоги до даним, обумовлені використанням алгоритму Вольфа, варіюють залежно від складності системи. Як мінімум, нам потрібно 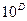 крапок і 10
крапок і 10 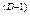 орбітальних періодів. Тому, якщо розмірність аттрактора дорівнює 2, то необхідно 100 точок даних; якщо ж розмірність рівна 6, то потрібний один мільйон крапок. Визначення розмірності є вирішальною умовою, якщо робиться спроба розрахунку показника Ляпунова.
орбітальних періодів. Тому, якщо розмірність аттрактора дорівнює 2, то необхідно 100 точок даних; якщо ж розмірність рівна 6, то потрібний один мільйон крапок. Визначення розмірності є вирішальною умовою, якщо робиться спроба розрахунку показника Ляпунова.
Модифікуємо алгоритм, щоб він став більш зручним для програмування.
Показник Ляпунова показує степінь залежності системи від початкових умов, і є мірою того, наскільки швидко дві фазові криві розбігаються у фазовому просторі. Система, реконструйована методом часових затримок із однієї фазової координати системи зберігає дисипативність, хаотичність, топологічні інваріанти аттрактора (фрактальна розмірність), якщо m ≥ 2 [d] +1 , m – розмірність простору вкладень, d- фрактальна розмірність.
Нехай x(t), t= 1..N – виміри однієї координати хаотичного процесу, виміряні через рівні проміжки часу. Після реконструкції системи та визначення розмірності простору вкладень, часової затримки отримаємо набір точок простору Rm: 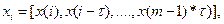
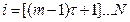 .
.
Виберемо із послідовності точку довільну x0 та знайдемо для неї таку 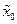 , щоб виконувалося ||
, щоб виконувалося || 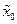 - x0|| = ε0 < ε , де ε – фіксована величина, що менша розміру реконструйованого аттрактору. Відслідковуємо еволюцію вибраних точок на реконструйованому аттракторі, доки відстань між ними не перевищуватиме заданої величини εmax. Позначимо отримані точки через x1 та
- x0|| = ε0 < ε , де ε – фіксована величина, що менша розміру реконструйованого аттрактору. Відслідковуємо еволюцію вибраних точок на реконструйованому аттракторі, доки відстань між ними не перевищуватиме заданої величини εmax. Позначимо отримані точки через x1 та  , відстань між ними через
, відстань між ними через 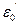 , а проміжок еволюції через T1.
, а проміжок еволюції через T1.
Далі, продивляючись послідовність, написану вище, знаходимо таку точку 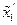 , щоб вона була близькою до x1, тобто ||
, щоб вона була близькою до x1, тобто || 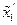 - x1|| = ε1 < ε , а вектори
- x1|| = ε1 < ε , а вектори  - x1 та
- x1 та 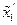 - x1 мали, по можливості, однакові напрямки.
- x1 мали, по можливості, однакові напрямки.
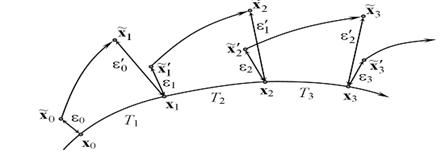
Мал.10. Оцінка найбільшого показника Ляпунова за часовим рядом.
Повторивши процедуру М разів на всьому наборі точок, можна оцінити старший показник Ляпунова за формулою:
Експоненціальне розходження двох випадково вбраних точок на аттракторі з одиничною імовірністю характеризує старший показник Ляпунова (за теоремою В.І. Оселедця)


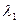 за експериментальними даними. Показник
за експериментальними даними. Показник 

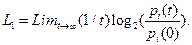 У реальності ми повинні мати справу з обмеженою кількістю зашумленных даних — це означає, що розмірність вкладення, часовий лаг і допустимі максимальне і мінімальні дистанції між точками повинні вибиратися з обачністю.
У реальності ми повинні мати справу з обмеженою кількістю зашумленных даних — це означає, що розмірність вкладення, часовий лаг і допустимі максимальне і мінімальні дистанції між точками повинні вибиратися з обачністю.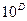 крапок і 10
крапок і 10 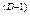 орбітальних періодів. Тому, якщо розмірність аттрактора дорівнює 2, то необхідно 100 точок даних; якщо ж розмірність рівна 6, то потрібний один мільйон крапок. Визначення розмірності є вирішальною умовою, якщо робиться спроба розрахунку показника Ляпунова.
орбітальних періодів. Тому, якщо розмірність аттрактора дорівнює 2, то необхідно 100 точок даних; якщо ж розмірність рівна 6, то потрібний один мільйон крапок. Визначення розмірності є вирішальною умовою, якщо робиться спроба розрахунку показника Ляпунова.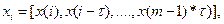
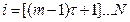 .
.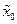 , щоб виконувалося ||
, щоб виконувалося ||  , відстань між ними через
, відстань між ними через 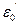 , а проміжок еволюції через T1.
, а проміжок еволюції через T1.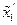 , щоб вона була близькою до x1, тобто ||
, щоб вона була близькою до x1, тобто ||