Як відомо, для режиму динамічного хаосу характерна наявність експоненціальної нестійкості траєкторій, кількісною мірою якої є позитивний показник Ляпунова, що характеризує ступінь чутливості системи до вибору початкових умов. Число позитивних експонент в спектрі показників Ляпунова визначається кількістю нестійких напрямів періодичних орбіт, вбудованих в хаотичний аттрактор, хоча в принципі можливі і складніші ситуації (що полягають в співіснуванні періодичних орбіт з різним числом нестійких напрямів). Ми обмежимося розглядом динамічних систем з одним позитивним показником Ляпунова  . При обчисленні
. При обчисленні  робиться припущення про "типовість" фазової траєкторії, що є вирішенням динамічної системи за вибраних початкових умов. Інакше величина показника, визначена на інтервалі часу
робиться припущення про "типовість" фазової траєкторії, що є вирішенням динамічної системи за вибраних початкових умов. Інакше величина показника, визначена на інтервалі часу  , може відрізнятися від граничного значення
, може відрізнятися від граничного значення  (відповідного
(відповідного 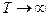 ). Зокрема, відомі випадки, коли дискретні моделі демонструють дуже тривалі перехідні процеси (до 1,500,000 ітерацій динаміка є "хаотичними", після чого стає регулярною). З погляду обчислення показника Ляпунова це відповідає тому, що величина
). Зокрема, відомі випадки, коли дискретні моделі демонструють дуже тривалі перехідні процеси (до 1,500,000 ітерацій динаміка є "хаотичними", після чого стає регулярною). З погляду обчислення показника Ляпунова це відповідає тому, що величина  протягом перехідного процесу сходиться до деякого позитивного значення, і лише на дуже тривалих часах спадає до нуля. Щоб охарактеризувати поведінку типової фазової траєкторії, іноді використовують поняття " показників Ляпунова на кінцевому часі" (finite time Lyapunov exponents), які характеризують швидкість розгону або стиснення по різних напрямах протягом кінцевого інтервалу часу
протягом перехідного процесу сходиться до деякого позитивного значення, і лише на дуже тривалих часах спадає до нуля. Щоб охарактеризувати поведінку типової фазової траєкторії, іноді використовують поняття " показників Ляпунова на кінцевому часі" (finite time Lyapunov exponents), які характеризують швидкість розгону або стиснення по різних напрямах протягом кінцевого інтервалу часу  .
.
Якщо рівняння динамічної системи, що генерує фазову траєкторію, відомі, то визначити величину максимального показника (або повний спектр показників Ляпунова) можна за допомогою добре відомого алгоритму, запропонованого в роботі Бенеттіна із співавторами (незалежно схожу техніку запропонували Шимада і Нагашима). Даний метод часто називають стандартним алгоритмом розрахунку показники Ляпунова.
Розглянемо систему однорідних диференціальних рівнянь:
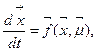
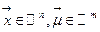 у якій
у якій 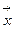 - вектор стану
- вектор стану 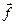 - нелінійна вектор-функція
- нелінійна вектор-функція 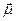 - вектор параметрів, що управляють. Дослідження даної системи на стійкість її часткового рішення
- вектор параметрів, що управляють. Дослідження даної системи на стійкість її часткового рішення 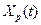 зводиться до аналізу рівнянь у варіаціях і введення поняття k-вимірного показника Ляпунова. Проте якщо обмежитися тільки обчисленням старшого показника Ляпунова, даний алгоритм істотно спрощується. Шукана величина
зводиться до аналізу рівнянь у варіаціях і введення поняття k-вимірного показника Ляпунова. Проте якщо обмежитися тільки обчисленням старшого показника Ляпунова, даний алгоритм істотно спрощується. Шукана величина  визначатиме еволюцію в часі вектора збурення
визначатиме еволюцію в часі вектора збурення 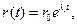 де
де 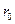 - величина початкового збурення (у момент часу
- величина початкового збурення (у момент часу 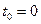 ),
), 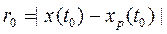 . Дана формула є дуже наближеною, оскільки швидкість розгону траєкторій не є постійною, а залежить від вибору точки на аттракторі. Строго кажучи, показники Ляпунова визначають шляхом вирішення рівнянь у варіаціях, розглядаючи нескінченно малі збурення. Проте існують роботи, в яких обґрунтовано, що експоненціальний закон розбігання траєкторій справедливий не тільки для нескінченно малих збурень, але і для малих збурень кінцевої величини, тому остання формула цілком може бути використана при практичному аналізі локальної нестійкості. Оскільки великі значення
. Дана формула є дуже наближеною, оскільки швидкість розгону траєкторій не є постійною, а залежить від вибору точки на аттракторі. Строго кажучи, показники Ляпунова визначають шляхом вирішення рівнянь у варіаціях, розглядаючи нескінченно малі збурення. Проте існують роботи, в яких обґрунтовано, що експоненціальний закон розбігання траєкторій справедливий не тільки для нескінченно малих збурень, але і для малих збурень кінцевої величини, тому остання формула цілком може бути використана при практичному аналізі локальної нестійкості. Оскільки великі значення 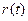 приймати не може (інакше не виконуватиметься умова лінійного наближення), при розрахунку старшого показника Ляпунова проводять перенормування, в ході якого задаються нові збурення, - малі по величині, але вибрані в напрямі, який відповідає вектору збурення безпосередньо перед перенормуванням. Потім знов оцінюють швидкість експоненціального розбігання довколишніх траєкторій. В результаті обчислюється усереднена уздовж фазової траєкторії
приймати не може (інакше не виконуватиметься умова лінійного наближення), при розрахунку старшого показника Ляпунова проводять перенормування, в ході якого задаються нові збурення, - малі по величині, але вибрані в напрямі, який відповідає вектору збурення безпосередньо перед перенормуванням. Потім знов оцінюють швидкість експоненціального розбігання довколишніх траєкторій. В результаті обчислюється усереднена уздовж фазової траєкторії 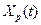 кількісна характеристика ступеня хаотичності. Схемний процедура перенормування зображена на рис. 5
кількісна характеристика ступеня хаотичності. Схемний процедура перенормування зображена на рис. 5
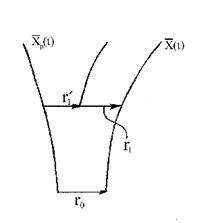
Рис. 5. Процедура перенормування для розрахунку старшого показника Ляпунова
Опишемо цю процедуру для розглянутої вище динамічної системи (1.3): 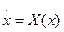 Процедура обчислення старшого ляпуновського показника починається з побудови чисельного методу рішення системи (1.3) на інтервалі часу, достатньому для того, щоб мати впевненість у виході траєкторії х(t) на аттрактор, тобто відкидаються фазові координати траєкторії, що відповідають перехідному процесу. Тривалість перехідного процесу не підкорюється яким-небудь загальним закономірностям і тому її приходиться визначати індивідуально для кожної конкретної задачі. В якості розрахункового чисельного методу частіше всього застосовують метод Рунге-Кутти 4 чи 5 порядку. Для збільшення точності обчислення потрібно використовувати змінний часовий крок відліку, проводячи корекцію цього кроку із застосуванням коректуючої процедури Дормана-Пріса. Це дозволяє добитися локальної похибки обчислення порядку О(10-15). Кінцеву точку цього відліку позначимо через х0 і приймаємо її за початкову точку траєкторії на аттракторі. Потім виводимо систему рівнянь першого наближення:
Процедура обчислення старшого ляпуновського показника починається з побудови чисельного методу рішення системи (1.3) на інтервалі часу, достатньому для того, щоб мати впевненість у виході траєкторії х(t) на аттрактор, тобто відкидаються фазові координати траєкторії, що відповідають перехідному процесу. Тривалість перехідного процесу не підкорюється яким-небудь загальним закономірностям і тому її приходиться визначати індивідуально для кожної конкретної задачі. В якості розрахункового чисельного методу частіше всього застосовують метод Рунге-Кутти 4 чи 5 порядку. Для збільшення точності обчислення потрібно використовувати змінний часовий крок відліку, проводячи корекцію цього кроку із застосуванням коректуючої процедури Дормана-Пріса. Це дозволяє добитися локальної похибки обчислення порядку О(10-15). Кінцеву точку цього відліку позначимо через х0 і приймаємо її за початкову точку траєкторії на аттракторі. Потім виводимо систему рівнянь першого наближення:
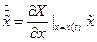 (1.9)
(1.9)
Далі будемо спільно вирішувати системи рівнянь (1.3) та (1.9). Причому для системи рівнянь (1.3) в якості початкової точки беремо х0, а для системи (1.9) – деяку точку 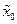 , для якої виконується відношення ||
, для якої виконується відношення || 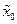 || = 1. Наприклад, в якості початкового вектору збурень можна взяти вектор
|| = 1. Наприклад, в якості початкового вектору збурень можна взяти вектор 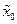 = {1,0,0,0,…,0}. Задамо деякий часовий інтервал Т і вирішимо чисельно системи (1.9) та (1.3), знайшовши вектор стану та його збурення в момент часу Т: х(Т) = х1,
= {1,0,0,0,…,0}. Задамо деякий часовий інтервал Т і вирішимо чисельно системи (1.9) та (1.3), знайшовши вектор стану та його збурення в момент часу Т: х(Т) = х1, 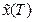 =
=  .
.
Тепер перевизначимо вектор збурення так, щоб його направлення залишалося незмінними, а норма дорівнювала вихідному значенню 1, тобто покладемо  . Необхідність такого перенумерування пов’язана з тим, що у випадку, коли траєкторія є нестійкою (наприклад, належить дивному аттрактору), амплітуда збурення дуже швидко прямує до нескінченості і без виконання перенумерування буде переповнення регістрів комп’ютера, в наслідок чого комп’ютер зависне.
. Необхідність такого перенумерування пов’язана з тим, що у випадку, коли траєкторія є нестійкою (наприклад, належить дивному аттрактору), амплітуда збурення дуже швидко прямує до нескінченості і без виконання перенумерування буде переповнення регістрів комп’ютера, в наслідок чого комп’ютер зависне.
Далі знову продовжимо процедуру чисельного рішення системи (1.3) з початковою точкою х1 і системи (1.9) з початковою точкою 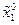 . Знайшовши вектор стану і вектор збурення в момент 2Т: х(2Т) = х2,
. Знайшовши вектор стану і вектор збурення в момент 2Т: х(2Т) = х2,  , перевизначимо вектор збурення
, перевизначимо вектор збурення 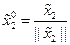 . Потім багато раз повторимо аналогічну процедуру знаходження рішень перенумерування.
. Потім багато раз повторимо аналогічну процедуру знаходження рішень перенумерування.
Якісно алгоритм Бенеттіні можна проілюструвати за допомогою малюнку 6.
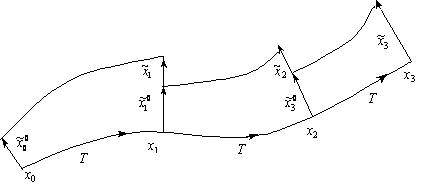
Рис. 6. Якісна схема алгоритму Бенеттіні .
Якщо початкова точка х0 належить типовій траєкторії аттрактора, а початкове збурення 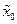 взято на наздогад, то еволюція амплітуди збурення буде визначатися, очевидно, старшим ляпуновським характерестичним показником. В силу формули (1.8) приблизно отримуємо:
взято на наздогад, то еволюція амплітуди збурення буде визначатися, очевидно, старшим ляпуновським характерестичним показником. В силу формули (1.8) приблизно отримуємо:
 (2.0)
(2.0)
При цьому число кроків К повинно бути достатньо великим. Практично ми закінчуємо чисельне обчислення, коли значення величини  стає незмінним відносно якої-небудь, наперед вибраної, кількості знаків після десяткової роздільної точки. Далі описану процедуру бажано повторити декілька раз з різними початковими умовами для вектору стану і вектору збурення і провести статистичну обробку отриманих результатів. Довжина інтервалу перенумерування Т вибирається індивідуально для кожної конкретної задачі.
стає незмінним відносно якої-небудь, наперед вибраної, кількості знаків після десяткової роздільної точки. Далі описану процедуру бажано повторити декілька раз з різними початковими умовами для вектору стану і вектору збурення і провести статистичну обробку отриманих результатів. Довжина інтервалу перенумерування Т вибирається індивідуально для кожної конкретної задачі.
Для обчислення інших ляпуновських показників необхідно розрахувати еволюцію відповідного числа векторів збурення вздовж фазової траєкторії, що розглядається. Якщо проводити обчислення за алгоритмом Бенеттіні, то в кожному векторі збурення, при достатньо великому часу чисельного обчислення, буде домінувати складова з максимальним ляпуновським показником.
5. Перетин і відображення Пуанкаре
Розглянемо динамічну систему із неперервним часом, динаміка, якої описується деякими диференціальними рівняннями.
Нехай, для визначеності, це система із трьохвимірним фазовим простором виду:
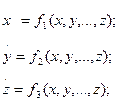 (2.1)
(2.1)
Далі розглянемо деякий розв’язок системи (2.1), якому відповідає у фазовому просторі траєкторія Г. Помістимо у фазовому просторі деяку площину S, рівняння якої має вигляд:
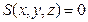 (2.2)
(2.2)
Вибір такої плоскості досить довільний, однак вона повинна розміщуватися так, щоб траєкторія Г багато разів її перетинала і дотикання траєкторії з площиною було неможливе (трансверсальний перетин). Така плоскість Sназивається січною Пуанкаре фазової траєкторії Г. Позначимо точки перетину траєкторії Г з січною Sчерез 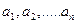 (Мал. 7). Відмітимо, що послідовність точок
(Мал. 7). Відмітимо, що послідовність точок 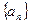 задається перетином Г з S в одному напрямі. Отримана дискретна множина точок
задається перетином Г з S в одному напрямі. Отримана дискретна множина точок 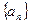 ,п = 1,2,3..., на січній Пуанкаре називається перетином Пуанкаре для траєкторії Г.
,п = 1,2,3..., на січній Пуанкаре називається перетином Пуанкаре для траєкторії Г.
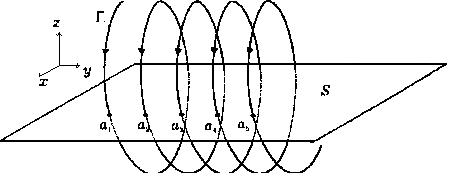
Мал. 7. Перетин Пуанкаре
Перетин Пуанкаре також породжує деяке дискретне відображення, яке ставить у відповідність будь-якій точці 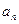 найближчу наступну за нею точку
найближчу наступну за нею точку 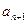 .
.
Закон відповідності між попередньою і наступною точками перетину Пуанкаре називається відображенням наслідування або відображенням Пуанкаре. Для даного тривимірного випадку, що розглядається це відображення буде вже двовимірним:
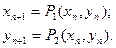 (2.3)
(2.3)
так, як точки перетину Пуанкаре розташовуються на площині і третю координату завжди можна виразити через дві перші.
Таким чином, задача вивчення динамічної системи (2.1)може бути зведена до задачі вивчення відповідного відображення Пуанкаре, якемає розмірність, на одиницю меншу, ніж розмірність початкової динамічної системи. При цьому структура динамічної системи однозначно (але не взаємно-однозначно) визначає структуру породжуваного нею дискретного відображення (2.3).Ця заміна об'єкту дослідження не супроводжується якими-небудь апроксимаціями, аналіз залишається точним. Однак при такій заміні об'єкту дослідження ми втрачаємо інформацію про характер динаміки в проміжках часу між послідовними перетинами січної площини, зокрема, про тривалість інтервалів часу між цими перетинами і про топологічні властивості фазової траєкторії. Проте зберігається можливість аналізувати багато принципових питань, наприклад, виникає в системі регулярний або хаотичний режим.
Нехай дискретні рівняння (2.3)є відображенням Пуанкаре диференціальних рівнянь (2.1).Припустимо, 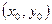 – стійка нерухома точка цього відображення. Їй відповідатиме стійкий однотактний граничний цикл системи (2.1).
– стійка нерухома точка цього відображення. Їй відповідатиме стійкий однотактний граничний цикл системи (2.1).
Припустимо, дискретні рівняння (2.3)мають періодичний розв’язок:
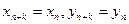 (2.4)
(2.4)
де 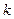 – дискретний період. Такий розв’язок називатимемо
– дискретний період. Такий розв’язок називатимемо 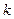 -циклом. Тоді
-циклом. Тоді 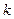 -циклу відображенню відповідатиме більш складніший
-циклу відображенню відповідатиме більш складніший 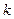 -тактний граничний цикл системи (2.1).Причому спектр ЛХП такого
-тактний граничний цикл системи (2.1).Причому спектр ЛХП такого 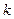 -цикла дискретного відображення (2.3), доповнений нульовим показником, збігається із спектром ЛХП системи.
-цикла дискретного відображення (2.3), доповнений нульовим показником, збігається із спектром ЛХП системи.
Якщо розв’язком дискретної системи (2.3) є квазіперіодична або хаотична послідовність, то відповідно квазіперіодичний або хаотичний режим встановлюватиметься в системі диференціальних рівняння (2.1).При цьому спектри ЛХП квазіперіодичних і хаотичних відображень збігаються з відповідними спектрами ЛХП квазіперіодичних або хаотичних аттракторів системи (2.1) за винятком одного нульового показника .
Знайти відображення Пуанкаре для конкретних нелінійних систем в явному вигляді вдається дуже рідко, в тих виняткових випадках, коли диференціальні рівняння допускають аналітичне рішення. Проте можна побудувати відображення Пуанкаре як чисельний алгоритм. При цьому виникають дві самостійні задачі. Перша – це знаходження деякої траєкторії Г системи (2.1) за заданих початкових умовах. Друга – це визначення координат точок перетину траєкторії з січною площиною, тобто побудова перетину і відображення Пуанкаре. Обчислити траєкторію можна за допомогою будь-якого відомого чисельного методу. Як уже відзначалося, для цього найчастіше застосовуються методи Рунге-Кутти. А для визначення точок перетину траєкторії з січною площиною необхідно на кожному кроці чисельного інтегрування системи (2.1) обчислювати значення функції S(x,y,z) до тих пір, поки не буде зафіксований момент зміни знаку S(x,y, z), який відповідає моменту перетину траєкторією січної площини.
Наприклад, нехай зміна знаку функції S(x,y,z) відбулася між n-м і (n +1) кроком, так що величини 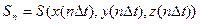 і
і 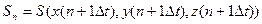 де
де 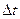 – крок чисельної інтеграції, мають різні знаки, як показано на мал. 7. Далі необхідно уточнити значення точки перетину
– крок чисельної інтеграції, мають різні знаки, як показано на мал. 7. Далі необхідно уточнити значення точки перетину 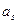 . Цю задачу можна розв’язати із заданою ступінь точності, застосувавши методи інтерполяції. Послідовно зменшуючи крок інтегрування в два рази, можливо закінчити обчислення, коли різниця
. Цю задачу можна розв’язати із заданою ступінь точності, застосувавши методи інтерполяції. Послідовно зменшуючи крок інтегрування в два рази, можливо закінчити обчислення, коли різниця 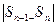 буде менше наперед заданої величини, яка визначає точність розрахунку точок
буде менше наперед заданої величини, яка визначає точність розрахунку точок 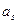 . Принципових труднощів тут немає, проте зростаючі вимоги до точності визначення
. Принципових труднощів тут немає, проте зростаючі вимоги до точності визначення 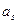 потребують додаткових обчислень, що ускладнить відповідні алгоритми обчислення і значно збільшить час, необхідний для розрахунків.
потребують додаткових обчислень, що ускладнить відповідні алгоритми обчислення і значно збільшить час, необхідний для розрахунків.
Для подолання цих складнощів М. Ено був запропонований простий і економічний метод, який полягає в наступному. Доповнимо систему рівнянь (2.1) ще одним співвідношенням, а саме
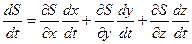
так як  , то враховуючи (2.1), можемо записати
, то враховуючи (2.1), можемо записати
 (2.5)
(2.5)
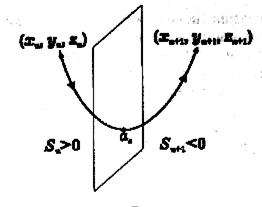
мал. 8
Введемо для зручності позначення

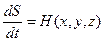
Тоді, враховуючи, що
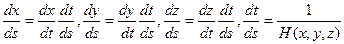
можемо записати
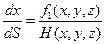
 (2.6)
(2.6)
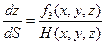
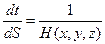
Візьмемо значення х, y, z, t і S, отримані на (n +1) кроці чисельного інтегрування і зробимо ще один крок по S, величина якого рівна
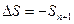
В результаті інтеграції системи (2.1) тільки на одному кроці 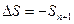 ми відразу попадаємо на січну S, причому похибка визначення точки перетину строго дорівнює погрішності інтеграції системи (2.1) на одному кроці і буде мінімальною. При знаходженні інших точок перетину (якщо вони існують) траєкторією Г плоскості S кожного разу інтегруватимемо систему (2.6) на одному кроці
ми відразу попадаємо на січну S, причому похибка визначення точки перетину строго дорівнює погрішності інтеграції системи (2.1) на одному кроці і буде мінімальною. При знаходженні інших точок перетину (якщо вони існують) траєкторією Г плоскості S кожного разу інтегруватимемо систему (2.6) на одному кроці 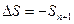 який змінюватиметься для кожної нової точки перетину.
який змінюватиметься для кожної нової точки перетину.
Алгоритм побудови відображення Пуанкаре по методу Ено зручно програмувати спочатку як чисельний розв’язок рівнянь (2.6). При цьому функція 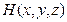 вважається рівною одиниці до тих пір, поки виконуються стандартні кроки за часом, і перевизначається відповідно до (2.5), коли виникає необхідність провести нестандартний крок по S. Оскільки в обох випадках використовується один і той же чисельний метод, досягається бажане узгодження по точності.
вважається рівною одиниці до тих пір, поки виконуються стандартні кроки за часом, і перевизначається відповідно до (2.5), коли виникає необхідність провести нестандартний крок по S. Оскільки в обох випадках використовується один і той же чисельний метод, досягається бажане узгодження по точності.
Всі проведені міркування очевидним чином поширюються на фазовий простір більшої розмірності, тільки замість січної двовимірної плоскості необхідно використовувати перетин n-вимірного фазового простору гіперповерхнею розмірності n-1. Та обставина, що при використанні відображення Пуанкаре розмірність зменшується на одиницю, інколи буває дуже корисною.
Метод перетину Пуанкаре особливо наочний у випадку п=3, коли множина точок перетину лежить на двовимірній поверхні. Для п>4 графічне представлення багатовимірного перетину Пуанкаре втрачає наочність. У цих випадках аналізують двох- або тривимірні проекції перетинів Пуанкаре.
Для періодичних розв’язків динамічної системи перетин Пуанкаре, як багатовимірний, так і його проекції, містять кінцеве число нерухомих точок, які повторюються строго через період розвязку. У режимі дивного аттрактора на січній з'явиться деяка хаотична множина точок, число яких зростатиме із зростанням часу чисельної інтеграції. В деяких випадках ця хаотична множина може розташовуватися уздовж тонкої стрічки, близької по структурі до одновимірної кривої на січній. Цю криву приблизно можна прийняти за відображення Пуанкаре і аналізувати методом діаграм Ламерея.
Слід зазначити, що при вивченні хаотичних режимів достовірну інформацію про структуру перетину Пуанкаре можна отримати тільки при досить великому числі точок в перетині Пуанкаре.


 . При обчисленні
. При обчисленні  , може відрізнятися від граничного значення
, може відрізнятися від граничного значення 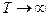 ). Зокрема, відомі випадки, коли дискретні моделі демонструють дуже тривалі перехідні процеси (до 1,500,000 ітерацій динаміка є "хаотичними", після чого стає регулярною). З погляду обчислення показника Ляпунова це відповідає тому, що величина
). Зокрема, відомі випадки, коли дискретні моделі демонструють дуже тривалі перехідні процеси (до 1,500,000 ітерацій динаміка є "хаотичними", після чого стає регулярною). З погляду обчислення показника Ляпунова це відповідає тому, що величина 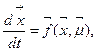
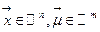 у якій
у якій 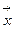 - вектор стану
- вектор стану 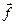 - нелінійна вектор-функція
- нелінійна вектор-функція 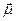 - вектор параметрів, що управляють. Дослідження даної системи на стійкість її часткового рішення
- вектор параметрів, що управляють. Дослідження даної системи на стійкість її часткового рішення 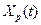 зводиться до аналізу рівнянь у варіаціях і введення поняття k-вимірного показника Ляпунова. Проте якщо обмежитися тільки обчисленням старшого показника Ляпунова, даний алгоритм істотно спрощується. Шукана величина
зводиться до аналізу рівнянь у варіаціях і введення поняття k-вимірного показника Ляпунова. Проте якщо обмежитися тільки обчисленням старшого показника Ляпунова, даний алгоритм істотно спрощується. Шукана величина 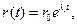 де
де 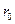 - величина початкового збурення (у момент часу
- величина початкового збурення (у момент часу 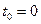 ),
), 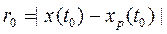 . Дана формула є дуже наближеною, оскільки швидкість розгону траєкторій не є постійною, а залежить від вибору точки на аттракторі. Строго кажучи, показники Ляпунова визначають шляхом вирішення рівнянь у варіаціях, розглядаючи нескінченно малі збурення. Проте існують роботи, в яких обґрунтовано, що експоненціальний закон розбігання траєкторій справедливий не тільки для нескінченно малих збурень, але і для малих збурень кінцевої величини, тому остання формула цілком може бути використана при практичному аналізі локальної нестійкості. Оскільки великі значення
. Дана формула є дуже наближеною, оскільки швидкість розгону траєкторій не є постійною, а залежить від вибору точки на аттракторі. Строго кажучи, показники Ляпунова визначають шляхом вирішення рівнянь у варіаціях, розглядаючи нескінченно малі збурення. Проте існують роботи, в яких обґрунтовано, що експоненціальний закон розбігання траєкторій справедливий не тільки для нескінченно малих збурень, але і для малих збурень кінцевої величини, тому остання формула цілком може бути використана при практичному аналізі локальної нестійкості. Оскільки великі значення 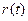 приймати не може (інакше не виконуватиметься умова лінійного наближення), при розрахунку старшого показника Ляпунова проводять перенормування, в ході якого задаються нові збурення, - малі по величині, але вибрані в напрямі, який відповідає вектору збурення безпосередньо перед перенормуванням. Потім знов оцінюють швидкість експоненціального розбігання довколишніх траєкторій. В результаті обчислюється усереднена уздовж фазової траєкторії
приймати не може (інакше не виконуватиметься умова лінійного наближення), при розрахунку старшого показника Ляпунова проводять перенормування, в ході якого задаються нові збурення, - малі по величині, але вибрані в напрямі, який відповідає вектору збурення безпосередньо перед перенормуванням. Потім знов оцінюють швидкість експоненціального розбігання довколишніх траєкторій. В результаті обчислюється усереднена уздовж фазової траєкторії 
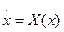 Процедура обчислення старшого ляпуновського показника починається з побудови чисельного методу рішення системи (1.3) на інтервалі часу, достатньому для того, щоб мати впевненість у виході траєкторії х(t) на аттрактор, тобто відкидаються фазові координати траєкторії, що відповідають перехідному процесу. Тривалість перехідного процесу не підкорюється яким-небудь загальним закономірностям і тому її приходиться визначати індивідуально для кожної конкретної задачі. В якості розрахункового чисельного методу частіше всього застосовують метод Рунге-Кутти 4 чи 5 порядку. Для збільшення точності обчислення потрібно використовувати змінний часовий крок відліку, проводячи корекцію цього кроку із застосуванням коректуючої процедури Дормана-Пріса. Це дозволяє добитися локальної похибки обчислення порядку О(10-15). Кінцеву точку цього відліку позначимо через х0 і приймаємо її за початкову точку траєкторії на аттракторі. Потім виводимо систему рівнянь першого наближення:
Процедура обчислення старшого ляпуновського показника починається з побудови чисельного методу рішення системи (1.3) на інтервалі часу, достатньому для того, щоб мати впевненість у виході траєкторії х(t) на аттрактор, тобто відкидаються фазові координати траєкторії, що відповідають перехідному процесу. Тривалість перехідного процесу не підкорюється яким-небудь загальним закономірностям і тому її приходиться визначати індивідуально для кожної конкретної задачі. В якості розрахункового чисельного методу частіше всього застосовують метод Рунге-Кутти 4 чи 5 порядку. Для збільшення точності обчислення потрібно використовувати змінний часовий крок відліку, проводячи корекцію цього кроку із застосуванням коректуючої процедури Дормана-Пріса. Це дозволяє добитися локальної похибки обчислення порядку О(10-15). Кінцеву точку цього відліку позначимо через х0 і приймаємо її за початкову точку траєкторії на аттракторі. Потім виводимо систему рівнянь першого наближення: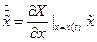 (1.9)
(1.9)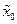 , для якої виконується відношення ||
, для якої виконується відношення || 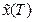 =
=  .
. . Необхідність такого перенумерування пов’язана з тим, що у випадку, коли траєкторія є нестійкою (наприклад, належить дивному аттрактору), амплітуда збурення дуже швидко прямує до нескінченості і без виконання перенумерування буде переповнення регістрів комп’ютера, в наслідок чого комп’ютер зависне.
. Необхідність такого перенумерування пов’язана з тим, що у випадку, коли траєкторія є нестійкою (наприклад, належить дивному аттрактору), амплітуда збурення дуже швидко прямує до нескінченості і без виконання перенумерування буде переповнення регістрів комп’ютера, в наслідок чого комп’ютер зависне.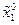 . Знайшовши вектор стану і вектор збурення в момент 2Т: х(2Т) = х2,
. Знайшовши вектор стану і вектор збурення в момент 2Т: х(2Т) = х2,  , перевизначимо вектор збурення
, перевизначимо вектор збурення 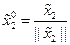 . Потім багато раз повторимо аналогічну процедуру знаходження рішень перенумерування.
. Потім багато раз повторимо аналогічну процедуру знаходження рішень перенумерування.
 (2.0)
(2.0)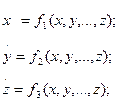 (2.1)
(2.1)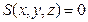 (2.2)
(2.2)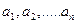 (Мал. 7). Відмітимо, що послідовність точок
(Мал. 7). Відмітимо, що послідовність точок 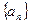 задається перетином Г з S в одному напрямі. Отримана дискретна множина точок
задається перетином Г з S в одному напрямі. Отримана дискретна множина точок 
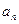 найближчу наступну за нею точку
найближчу наступну за нею точку 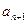 .
.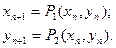 (2.3)
(2.3)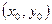 – стійка нерухома точка цього відображення. Їй відповідатиме стійкий однотактний граничний цикл системи (2.1).
– стійка нерухома точка цього відображення. Їй відповідатиме стійкий однотактний граничний цикл системи (2.1).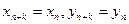 (2.4)
(2.4)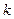 – дискретний період. Такий розв’язок називатимемо
– дискретний період. Такий розв’язок називатимемо 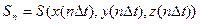 і
і 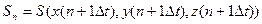 де
де 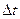 – крок чисельної інтеграції, мають різні знаки, як показано на мал. 7. Далі необхідно уточнити значення точки перетину
– крок чисельної інтеграції, мають різні знаки, як показано на мал. 7. Далі необхідно уточнити значення точки перетину 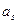 . Цю задачу можна розв’язати із заданою ступінь точності, застосувавши методи інтерполяції. Послідовно зменшуючи крок інтегрування в два рази, можливо закінчити обчислення, коли різниця
. Цю задачу можна розв’язати із заданою ступінь точності, застосувавши методи інтерполяції. Послідовно зменшуючи крок інтегрування в два рази, можливо закінчити обчислення, коли різниця 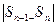 буде менше наперед заданої величини, яка визначає точність розрахунку точок
буде менше наперед заданої величини, яка визначає точність розрахунку точок 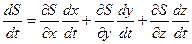
 , то враховуючи (2.1), можемо записати
, то враховуючи (2.1), можемо записати (2.5)
(2.5)

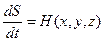
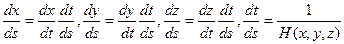
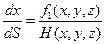
 (2.6)
(2.6)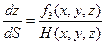
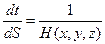
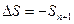
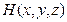 вважається рівною одиниці до тих пір, поки виконуються стандартні кроки за часом, і перевизначається відповідно до (2.5), коли виникає необхідність провести нестандартний крок по S. Оскільки в обох випадках використовується один і той же чисельний метод, досягається бажане узгодження по точності.
вважається рівною одиниці до тих пір, поки виконуються стандартні кроки за часом, і перевизначається відповідно до (2.5), коли виникає необхідність провести нестандартний крок по S. Оскільки в обох випадках використовується один і той же чисельний метод, досягається бажане узгодження по точності.