Розглянемо динамічну систему у векторній формі (1.3). Нехай x(t) – деяка фазова траєкторія цієї системи, яку ми будемо називати незбуреною. Далі, нехай 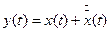 - близька до незбуреної траєкторії, що реалізується при незначній зміні початкових умов. Назвемо траєкторію
- близька до незбуреної траєкторії, що реалізується при незначній зміні початкових умов. Назвемо траєкторію 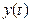 збуреною. Тоді еволюція малого збурення
збуреною. Тоді еволюція малого збурення 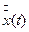 в лінійному наближенні описується рівнянням першого порядку:
в лінійному наближенні описується рівнянням першого порядку:
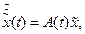 (1.4)
(1.4)
де матриця 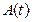 має вигляд:
має вигляд:

Для системи (1.4) має місце теорема:
Теорема Ляпунова.Нехай існує такаконстанта М, що для всіх елементів 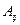 матриці А і для довільного Т
матриці А і для довільного Т
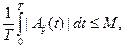
тоді:
1. Для будь-якого рішення 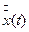 рівняння (1.4) існує ляпуновський характерестичний показник – дійсне число, що відрізняється від
рівняння (1.4) існує ляпуновський характерестичний показник – дійсне число, що відрізняється від 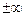 , яке визначається за формулою:
, яке визначається за формулою:
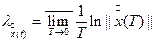 (1.5)
(1.5)
2. При множенні рішення на константу С ляпуновський характерестичний показник не міняється:
 (1.6)
(1.6)
3. Ляпуновський характеристичний показник лінійної комбінації двох рішень не перевищує більшого із показників цих двох рішень:
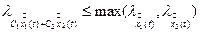 (1.7)
(1.7)
4. Існує n лінійно незалежних рішень 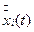 (фундаментальна система рішень рівняння (1.4), яким відповідають n лупуновських характеристичних показників, які нумеруються в порядку зменшення
(фундаментальна система рішень рівняння (1.4), яким відповідають n лупуновських характеристичних показників, які нумеруються в порядку зменшення 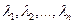 .
.
Набір чисел { 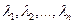 } спектром лупуновських характеристичних показників (ЛХП). Найбільше із цих чисел
} спектром лупуновських характеристичних показників (ЛХП). Найбільше із цих чисел  називається старшим лупуновським показником. Спектр ЛХП потрібно розглядати як характеристику лінійної системи рівнянь (1.4) в цілому, а не як одне рішення
називається старшим лупуновським показником. Спектр ЛХП потрібно розглядати як характеристику лінійної системи рівнянь (1.4) в цілому, а не як одне рішення 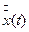 , оскільки рішення не залежить від вибору фундаментальної системи {
, оскільки рішення не залежить від вибору фундаментальної системи { 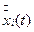 }.В силу (1.6) – (1.7) для будь-якого рішення
}.В силу (1.6) – (1.7) для будь-якого рішення 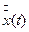 ляпуновським характеристичним показником обов’язково буду одне з чисел {
ляпуновським характеристичним показником обов’язково буду одне з чисел { 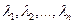 }.
}.
Модно довести, що для положення рівноваги системи (1.3) спектр ЛХП складається лише із дійсних частин власних чисел матриці системи першого наближення. Для граничного циклу системи (1.3) спектр ЛХП визначається за формулою:
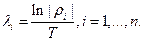
де 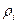 - мультиплікатор граничного циклу, а Т – його період.
- мультиплікатор граничного циклу, а Т – його період.
До цих пір, говорячи про спектр ЛХП, ми приписували його деякій фазовій траєкторії. Вирішимо тепер більш загальне питання про стійкість динамічної системи у встановленому режимі, що диктує нам необхідність визначення спектра ЛХП аттрактору. Якщо аттрактор представляє собою положення рівноваги чи граничний цикл, то він складається із однієї траєкторії і вже визначений нами спектр буде спектром ЛХП такого аттрактору. Якщо ж аттрактор складається із множини траєкторій, як, наприклад, тор чи дивний аттрактор, то виникає далеко не очевидне питання: чи можливо приписати аттрактору у цілому спектр якої-небудь траєкторії цього аттрактора.Тут на допомогу приходить мультиплікативна ергодична теореми В.І. Оселедця, що стверджує, що типова взята навмання траєкторія на аттракторі з одиничною імовірністю буде мати цілком визначений спектр ЛХП, який можна приписати аттрактору в цілому.
Спектр ЛХП аттрактора дисипативної динамічної системи повинен задовольняти наступним умовам:
1. Сума всіх n показників повинна бути від’ємною:

Це умова дисипативності, завдяки який аттрактор є притягуючою граничною множиною нульової міри в фазовому просторі.
2. У аттрактора, що не знаходиться в положенні рівноваги, обов’язково повинен бути хоча б один нулевий показник.
Нехай ляпуновські характеристичні показники впорядковані за спаданням. Будемо позначати додатній показник знаком ‘+’ , від’ємний – знаком ‘-’, а нулевий – нулем. Тоді аттрактору динамічної системи у фазовому просторі розмірності n буде відповідати набір із n знаків, який ми будемо називати сигнатурою спектра ЛХП. Дослідимо, які можуть бути сигнатури при різних розмірах фазового простору.
При n=1 можливий тільки один варіант сигнатури < - >, що відповідає аттрактору у вигляді нерухомої точки – асимптотично стійкому положенню рівноваги.
При n=2 можливі тільки два варіанти сигнатури:
< -,- > - стійке положення рівноваги;
< 0,- > - граничний цикл.
Покажемо, що при n=2 всі інші варіанти сигнатур неможливі. Дійсно, сигнатури <+,0 > , < 0,0 > неможливі, так як такі сигнатури суперечать умові дисипативності (сума ляпуновських показників не буде від’ємною). Варіант <+,- > також неможливий, так як положення рівноваги з такою сигнатурою не стійке і не є аттрактором. Якщо ж аттрактор не є положенням рівноваги, то така сигнатура виключена в силу обов’язковій наявності, в цьому випадку, нульового показника.
Можливість виникнення аттрактору з додатнім ляпуновським характеристичним показником виникає, починаючи із розмірності фазового простору n=3. Тут можливі такі варіанти сигнатур:
< -, - , - > - стійке положення рівноваги;
< 0, -, - > - граничний цикл;
< 0, 0 ,- > - двовимірний тор;
< +, 0, - > - дивний аттрактор.
Всі інші варіанти сигнатур суперечать чи умові дисипативності, чи - необхідності наявності нульового показника для аттракторів, які не є нерухомими точками, чи – визначенню аттрактора.
При збільшенні розмірності фазового простору число можливих варіантів сигнатур істотно збільшується. Наприклад, при n=4 крім дивного аттрактору з одним додатнім лупуновським показником < +, 0, - > може існувати дивний аттрактор з двома додатними показниками < +, +, 0, - >. Дивні аттрактори, які мають в спектрі ЛХП більше одного додатного показника, називаються гіперхаотичними.
Таким чином, для динамічних систем, що описуються автономними диференціальними рівняннями, ми прийшли до фундаментального висновку – принципіальна можливість реалізації дивного аттрактору починається з розмірності фазового простору n=3. На фазовій площині існування фазових аттракторів неможливе.
До речі, неможливість дивного аттрактору на площині може бути доведена такими простими міркуваннями. Кожен аттрактор, в тому числі і дивний, повинен бути стійким по Лагранжу (розташовується в обмеженій області фазового простору) і по Пуасону (зображуюча точка повинна нескінченну кількість раз повертатися в ε-окіл стартової точки траєкторій аттрактору). На фазовій площині це обов’язково приведе до самоперетину траєкторії, що суперечить теоремі Коші-Пікапа. Отже, дивний аттрактор на фазовій площині не може існувати.
Наявність в секторі ЛХП додатного показника є одним із основних критеріїв ідентифікації дивних аттракторів в конкретних прикладних динамічних системах. Тому дуже важливо вміти вираховувати спектр ЛХП чи хоча би старший показник спектру. Нажаль, для більшості практичних динамічних систем саме вираховування показника за формулою
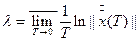 (1.8)
(1.8)
неможливе, так як траєкторія аттрактора не може бути знайдена для довільної системи за допомогою квадратурних формул. Тому для обчислення ляпуновських характеристичних показників приходиться застосовувати методи, основані на чисельних методах. Одним з найбільш відомих та застосованих методів є так званий алгоритм Бенеттіні та інших.


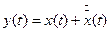 - близька до незбуреної траєкторії, що реалізується при незначній зміні початкових умов. Назвемо траєкторію
- близька до незбуреної траєкторії, що реалізується при незначній зміні початкових умов. Назвемо траєкторію 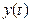 збуреною. Тоді еволюція малого збурення
збуреною. Тоді еволюція малого збурення 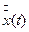 в лінійному наближенні описується рівнянням першого порядку:
в лінійному наближенні описується рівнянням першого порядку: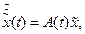 (1.4)
(1.4)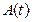 має вигляд:
має вигляд:
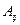 матриці А і для довільного Т
матриці А і для довільного Т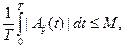
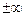 , яке визначається за формулою:
, яке визначається за формулою: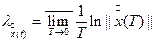 (1.5)
(1.5) (1.6)
(1.6)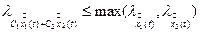 (1.7)
(1.7)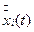 (фундаментальна система рішень рівняння (1.4), яким відповідають n лупуновських характеристичних показників, які нумеруються в порядку зменшення
(фундаментальна система рішень рівняння (1.4), яким відповідають n лупуновських характеристичних показників, які нумеруються в порядку зменшення 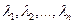 .
. називається старшим лупуновським показником. Спектр ЛХП потрібно розглядати як характеристику лінійної системи рівнянь (1.4) в цілому, а не як одне рішення
називається старшим лупуновським показником. Спектр ЛХП потрібно розглядати як характеристику лінійної системи рівнянь (1.4) в цілому, а не як одне рішення 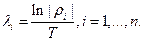
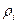 - мультиплікатор граничного циклу, а Т – його період.
- мультиплікатор граничного циклу, а Т – його період.
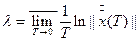 (1.8)
(1.8)