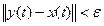Розглянемо динамічну систему, задану системою диференціальних рівнянь у векторному вигляді (1.3)
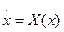 і припустимо, що її стан задається n-вимірним вектором х(t), а вектор-функція Х(х) відображає n-вимірний евклідовий простір
і припустимо, що її стан задається n-вимірним вектором х(t), а вектор-функція Х(х) відображає n-вимірний евклідовий простір 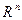 в себе. Як було встановлено в різних численних дослідженнях основним механізмом виникнення детермінованого хаосу є нестійкість по Ляпунову траєкторій аттрактора. Тому познайомимося із стійкістю по Ляпунову і іншими типами стійкості системи (1.3).
в себе. Як було встановлено в різних численних дослідженнях основним механізмом виникнення детермінованого хаосу є нестійкість по Ляпунову траєкторій аттрактора. Тому познайомимося із стійкістю по Ляпунову і іншими типами стійкості системи (1.3).
Точка х0, а також траєкторія х(t), що виходить з неї, називаються стійкими по Лагранжу, якщо траєкторія х(t) завжди, при всіх t>0, залишається в деякій обмеженій області фазового простору. Іншими словами, існує така константа М, що для всіх t>0 виконується нерівність || х(t)||< М, де || х(t)||, як правило, звичайна евклідова норма:
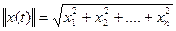 . Тут
. Тут 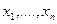 – компоненти вектора х.
– компоненти вектора х.
Точка n-вимірного фазового простору у називається  - граничною точкою фазової траєкторії х(t), якщо можна вказати таку послідовність моментів часу
- граничною точкою фазової траєкторії х(t), якщо можна вказати таку послідовність моментів часу 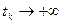 , що
, що 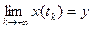 . Аналогічно точка z називається
. Аналогічно точка z називається 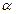 -граничною, якщо можна вказати таку послідовність моментів часу
-граничною, якщо можна вказати таку послідовність моментів часу 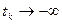 , що
, що 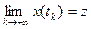 . Множина всіх
. Множина всіх 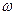 - граничних точок називається
- граничних точок називається 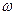 - граничною множиною даної траєкторії і позначається через
- граничною множиною даної траєкторії і позначається через 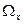 . Відповідно множина усіх
. Відповідно множина усіх 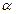 - граничних точок називається
- граничних точок називається 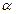 - граничною множиною даної траєкторії і позначається через
- граничною множиною даної траєкторії і позначається через 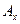 . Траєкторія x(t) називається стійкою по Пуассону, якщо кожна її точка є
. Траєкторія x(t) називається стійкою по Пуассону, якщо кожна її точка є  - граничною і
- граничною і 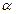 - граничною, тобто
- граничною, тобто 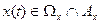 .
.
З визначення стійкості по Пуассону випливає, що будь-який сталий режим коливань (як регулярний, так і хаотичний) нелінійних дисипативних систем представляється траєкторіями стійкими по Пуассону. Зворотне твердження невірне.
Розглянемо декілька прикладів різних типів траєкторій. Найпростішою траєкторією є положення рівноваги. Така траєкторія складається тільки з однієї точки і, очевидно, стійка по Пуассону.
Якщо розглянути траєкторію, відмінну від нерухомої точки, то, як випливає з визначення, стійкою по Пуассону вона буде в тому випадку, якщо має властивість повертатися в як завгодно малий окіл кожної своєї точки нескінченне число раз. Повернення траєкторії в 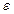 -окіл довільно вибраної на ній початкової точки називається поверненням Пуанкаре.
-окіл довільно вибраної на ній початкової точки називається поверненням Пуанкаре.
Тепер розглянемо граничний цикл. Очевидно, що повернення Пуанкаре в довільно вибрану початкову точку циклу фіксуватимуться періодично з як завгодно великою точністю. Час повернення Т в цьому випадку буде просто періодом циклу. Він не залежить від вибору 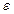 , принаймні, для достатньо малих
, принаймні, для достатньо малих 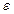 .
.
Розглянемо наступний приклад. Припустимо, що для будь-кого заданого 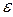 можна вказати період повернення Т(
можна вказати період повернення Т( 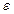 ), один і той же для довільної початкової точки на даній траєкторії, причому при
), один і той же для довільної початкової точки на даній траєкторії, причому при  цей період прямує до нескінченності. Отже, повернення з даним ступенем точності слідують один за одним регулярно, з правильною періодичністю, проте період зростає, якщо ми бажаємо збільшити точність порівняння станів. Як відомо, такі рухи називаються квазіперіодичними. Зокрема, до них належить суперпозиція двох періодичних коливань з раціонально не сумірними частотами. У фазовому просторі цьому типу руху відповідає траєкторія, яка усюди щільно покриває тороїдальну поверхню.
цей період прямує до нескінченності. Отже, повернення з даним ступенем точності слідують один за одним регулярно, з правильною періодичністю, проте період зростає, якщо ми бажаємо збільшити точність порівняння станів. Як відомо, такі рухи називаються квазіперіодичними. Зокрема, до них належить суперпозиція двох періодичних коливань з раціонально не сумірними частотами. У фазовому просторі цьому типу руху відповідає траєкторія, яка усюди щільно покриває тороїдальну поверхню.
І нарешті, детермінований хаос – це така ситуація, коли повернення Пуанкаре в 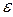 -окіл початкової точки відбуваються без ознак регулярності, а інтервал часу між двома послідовними поверненнями кожного разу інший. У результаті спостерігається деяка хаотична послідовність часу таких повернень. Хаотичність таких повернень може допомогти нам ідентифікувати той факт, що в динамічній системі існує дивний аттрактор.
-окіл початкової точки відбуваються без ознак регулярності, а інтервал часу між двома послідовними поверненнями кожного разу інший. У результаті спостерігається деяка хаотична послідовність часу таких повернень. Хаотичність таких повернень може допомогти нам ідентифікувати той факт, що в динамічній системі існує дивний аттрактор.
Відмітимо, що визначення стійкості по Лагранжу і Пуассону характеризують яку-небудь окремо взяту траєкторію і нічого не говорять про поведінку близьких до неї траєкторій. Така поведінка описує стійкість по Ляпунову. Припустимо, що система (1.1) при старті з точки х0 породжує траєкторію х(t), при старті з точки — траєкторію у(t). Траєкторія х(t) називається стійкою по Ляпунову, якщо для довільного, як завгодно малого  >0, існує таке
>0, існує таке  , що для будь-якої стартової точки у0, яка задовольняє нерівності
, що для будь-якої стартової точки у0, яка задовольняє нерівності
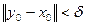 при всіх t>0 виконується нерівність
при всіх t>0 виконується нерівність 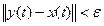
Таким чином, якщо дві траєкторії близькі в початковий момент часу, то вони залишаються близькими і в будь-який подальший момент часу.
Траєкторія х(t) називається асимптотично стійкою, якщо вона стійка по Ляпунову і 
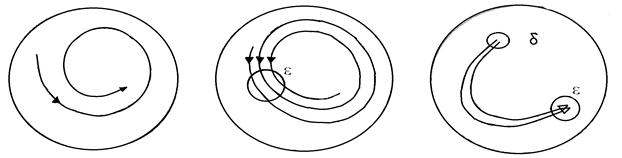
Наочна ілюстрація різних типів стійкості приведена на мал. 4 зліва показана траєкторія стійка по Лагранжу. Вона постійно залишається в замкнутій області. В центрі траєкторія стійка по Пуассону. Вона багато разів повертається в  -окіл початкової точки. Нарешті, справа траєкторія стійка по Ляпунову. Дві близькі в початковий момент часу траєкторії назавжди залишаються близькими.
-окіл початкової точки. Нарешті, справа траєкторія стійка по Ляпунову. Дві близькі в початковий момент часу траєкторії назавжди залишаються близькими.
а б в
Мал. 4. Стійкість по Лагранжу (а), Пуассону (б) і Ляпунову (в)
Має місце наступна теорема.
Теорема. Якщо неперіодична траєкторія стійка по Пуассону і по Ляпунову, то вона квазипериодична.
З цієї теореми відразу витікає, що всі регулярні аттрактори динамічних систем (положення рівноваги, граничні цикли і квазіперіодичні аттрактори) стійкі як по Пуассону, так і по Ляпунову. У свою чергу, всі дивні аттрактори динамічних систем стійкі по Пуассону і нестійкі по Ляпунову.


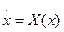 і припустимо, що її стан задається n-вимірним вектором х(t), а вектор-функція Х(х) відображає n-вимірний евклідовий простір
і припустимо, що її стан задається n-вимірним вектором х(t), а вектор-функція Х(х) відображає n-вимірний евклідовий простір 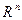 в себе. Як було встановлено в різних численних дослідженнях основним механізмом виникнення детермінованого хаосу є нестійкість по Ляпунову траєкторій аттрактора. Тому познайомимося із стійкістю по Ляпунову і іншими типами стійкості системи (1.3).
в себе. Як було встановлено в різних численних дослідженнях основним механізмом виникнення детермінованого хаосу є нестійкість по Ляпунову траєкторій аттрактора. Тому познайомимося із стійкістю по Ляпунову і іншими типами стійкості системи (1.3).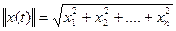 . Тут
. Тут 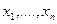 – компоненти вектора х.
– компоненти вектора х. - граничною точкою фазової траєкторії х(t), якщо можна вказати таку послідовність моментів часу
- граничною точкою фазової траєкторії х(t), якщо можна вказати таку послідовність моментів часу 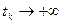 , що
, що 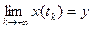 . Аналогічно точка z називається
. Аналогічно точка z називається 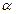 -граничною, якщо можна вказати таку послідовність моментів часу
-граничною, якщо можна вказати таку послідовність моментів часу 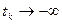 , що
, що 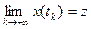 . Множина всіх
. Множина всіх 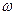 - граничних точок називається
- граничних точок називається 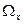 . Відповідно множина усіх
. Відповідно множина усіх 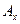 . Траєкторія x(t) називається стійкою по Пуассону, якщо кожна її точка є
. Траєкторія x(t) називається стійкою по Пуассону, якщо кожна її точка є 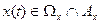 .
.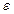 -окіл довільно вибраної на ній початкової точки називається поверненням Пуанкаре.
-окіл довільно вибраної на ній початкової точки називається поверненням Пуанкаре.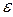 можна вказати період повернення Т(
можна вказати період повернення Т(  цей період прямує до нескінченності. Отже, повернення з даним ступенем точності слідують один за одним регулярно, з правильною періодичністю, проте період зростає, якщо ми бажаємо збільшити точність порівняння станів. Як відомо, такі рухи називаються квазіперіодичними. Зокрема, до них належить суперпозиція двох періодичних коливань з раціонально не сумірними частотами. У фазовому просторі цьому типу руху відповідає траєкторія, яка усюди щільно покриває тороїдальну поверхню.
цей період прямує до нескінченності. Отже, повернення з даним ступенем точності слідують один за одним регулярно, з правильною періодичністю, проте період зростає, якщо ми бажаємо збільшити точність порівняння станів. Як відомо, такі рухи називаються квазіперіодичними. Зокрема, до них належить суперпозиція двох періодичних коливань з раціонально не сумірними частотами. У фазовому просторі цьому типу руху відповідає траєкторія, яка усюди щільно покриває тороїдальну поверхню. >0, існує таке
>0, існує таке  , що для будь-якої стартової точки у0, яка задовольняє нерівності
, що для будь-якої стартової точки у0, яка задовольняє нерівності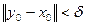 при всіх t>0 виконується нерівність
при всіх t>0 виконується нерівність