Электронные счетчики и делители частоты

На базе счетных триггеров можно построить цифровое устройство, получившее название электронного счетчика. Электронные счетчики ( далее, просто счетчики) позволяют вести подсчет электрических импульсов, количество которых (поступивших на вход счетчика) представляется, обычно, в параллельном коде. Счетчики могут отличаться модулем счета и типом счетной последовательности, которая, в частности, может быть двоичной, двоично-десятичной, в коде Грея и т.п. Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты. Таким образом, любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Так как счетчики и делители имеют единую структуру, основное внимание будет уделено синтезу счетчиков.

  Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.

  Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.

  Счетчики, независимо от способа синхронизации, подразделяются на счетчики прямого счета (суммирующие) и на счетчики обратного счета (вычитающие). В интегральном исполнении выпускаются также реверсивные счетчики, в которых имеется специальный вход для переключения режима работы, т.е. направления счета. Многие типы счетчиков, выпускаемые промышленностью в интегральном исполнении, имеют дополнительные входы предустановки, позволяющие использовать эти счетчики в режиме регистра памяти.

  В качестве разрядных триггеров счетчиков и делителей могут быть использованы двухступенчатые D-триггеры, Т- и JK-триггеры.

  Счетчики относятся к последовательностным устройствам с циклически повторяющейся последовательностью состояний. Число, соответствующее количеству импульсов (поступивших на вход счетчика), при котором счетчик “возвращается” в исходное состояние, называется модулем или коэффициентом счета. Модуль счета, обычно, обозначают буквой М (или К_сч). Например, максимальный модуль счета счетчика из двух триггеров равен М = 2² = 4, трех триггеров - М = 2³ = 8 и т.д. В общем случае для n - разрядного счетчика - М = 2ⁿ. Модуль счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 позволяет реализовать (без дополнительных схемных затрат) делитель частоты на 8. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.

  Асинхронный двоичный счетчик. Асинхронный двоичный счетчик представляет собой совокупность последовательно соединенных триггеров (D - или JK ), каждый из  которых  ассоциируется  с  битом в двоичном представлении числа. Если в счетчике m триггеров, то число возможных состояний счетчика равно 2^m, и, следовательно, модуль счета М также равен 2^m. Счетная последовательность в двоичном суммирующем счетчике начинается с нуля и доходит до максимального числа 2^m - 1, после чего снова проходит через нуль и повторяется. В вычитающем двоичном счетчике последовательные двоичные числа перебираются в обратном порядке, и при повторении последовательности максимальное число следует за нулем.

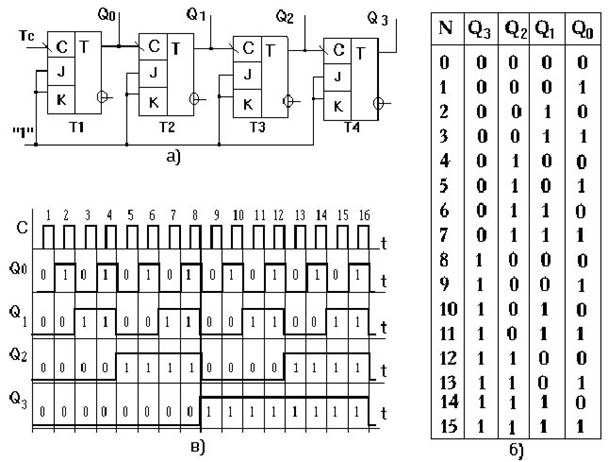
  Рассмотрим устройство двоичного суммирующего счетчика по модулю М=16, выполненного на базе JK-триггеров (рис. 3.33, а).

Как видно из рис. 3.33, (а), синхронизирующие входы всех триггеров, кроме крайнего левого (Т1), соединены с выходами предыдущих триггеров. Поэтому состояние триггера меняется в ответ на изменение состояния предыдущего триггера.

  Из таблицы состояния счетчика (рис. 3.33, б) легко заметить, что значение разряда в выбранной позиции меняется тогда, когда в соседней справа позиции состояние переходит из “1” в “0”, управление триггерами осуществляется задним фронтом синхроимпульсов (отрицательным перепадом напряжения импульса синхронизации).

Рис. 3.33. Схема а), таблица состояний триггеров б) и временные диаграммы, поясняющие работу в) последовательного четырехразрядного счетчика на

JK - триггерах

Временные диаграммы, поясняющие работу асинхронного суммирующего счетчика приведены на рис. 3.33, в.

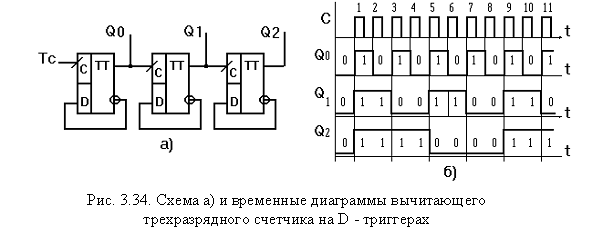
  Счетчики обратного счета (вычитающие счетчики). На рис. 3.34 приведена схема асинхронного трехразрядного двоичного вычитающего счетчика, построенного на базе D-триггеров. Отметим, что условия для изменения состояний триггеров вычитающих счетчиков аналогичны условиям для суммирующих счетчиков с той лишь разницей, что они должны “опираться” на значения инверсных, а не прямых выходов триггеров. Следовательно, рассмотренный выше счетчик можно превратить в вычитающий, просто переключив входы “С” триггеров с выходов Q на выходы . Когда в качестве разрядных триггеров используются D-триггеры, синхронизируемые передним фронтом синхроимпульсов, для получения вычитающего счетчика (асинхронного) входы “С” последующих тригеров соединяются с прямыми выходами предыдущих, также как в счетчике прямого счета, построенного на JK-триггерах.

   Работа вычитающего счетчика на D-триггерах наглядно иллюстрирована на рис. 3.34, (б). Из рис. 3.34 следует, что после нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние “1”. Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, снова, все триггеры обнуляются и цикл счета повторяется, что соответствует модулю М=8.

  В некоторых случаях необходимо, чтобы счетчик мог работать как в прямом, так и в обратном направлении счета. Такие счетчики называются реверсивными. Реверсивные счетчики могут быть как асинхронного, так и синхронного типа. Они строятся путем применения логических коммутаторов (мультиплексоров) в цепях связи между триггерами. Так, например, асинхронный реверсивный двоичный счетчик можно построить, если обеспечить подачу сигналов с прямого (при суммировании) или с инверсного (при вычитании) выхода пре-дыдущего JK- или Т-триггера на счетный вход последующего. В случае, когда реверсивный счетчик строится на базе D-триггеров, управляемых передним фронтом, для получения режима прямого счета следует соединить инверсный выход предыдущего с счетным входом последующего триггера.

  Все рассмотренные типы счетчиков могут быть использованы в цифровых устройствах “умеренного” быстродействия, когда частота следования синхроимпульсов не превышает критического значения, при котором время задержки установки триггеров последних (старших) разрядов счетчика становится соизмеримым с длительностью периода входных тактовых импульсов. В связи с этим, асинхронные счетчики строятся на относительно небольшое количество разрядов, так как при большем количестве разрядов выходные сигналы триггеров старших разрядов появляются позднее, чем управляющие фронты синхроимпульсов (поступающих на вход первого триггера) .

  Параллельные счетчики (синхронные счетчики). Как было уже сказано выше, параллельные счетчики бывают двух типов: синхронные параллельные и синхронные последовательные.

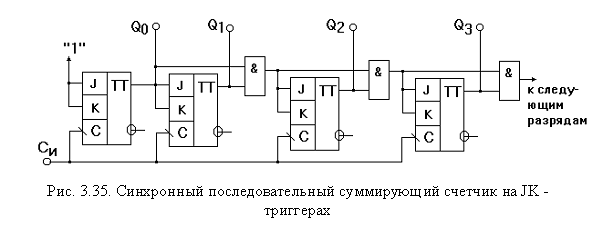
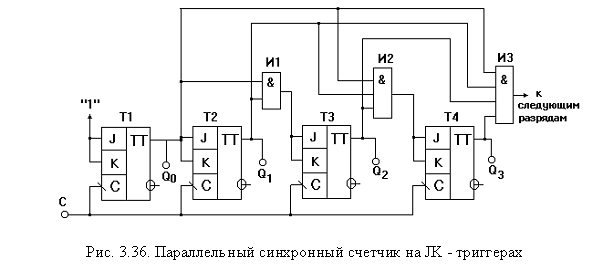
  Синхронный последовательный счетчик. По способу подачи синхроимпульсов такие счетчики параллельные, т.е. синхроимпульсы поступают на все триггеры счетчика параллельно, а по способу управления (подачи управляющих импульсов) - последовательные. Схема синхронного последовательного счетчика, реализованного на JK-триг-герах, приведена на рис. 3.35.

  Синхронный последовательный счетчик обладает повышенным быстродействием, однако, за счет последовательного формирования управляющих уровней, на входы “J” и “К” счетных триггеров, быстродействие несколько уменьшается. От этого недостатка лишены параллельные синхронные счетчики, в которых формирование управляющих уровней и их подача на соответствующие входы триггеров счетчика осуществляется одновременно, т.е. параллельно. Пример реализации параллельного синхронного счетчика иллюстрирован на рис. 3.36.

  Поскольку счетчик имеет одну общую линию синхронизации, состояние триггеров меняется синхронно, т.е. те триггеры, которые по синхроимпульсу должны изменить свое состояние, делают это одновременно, что существенно повышает быстродействие синхронных счетчиков.

  Счетчики с произвольным коэффициентом счета. Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.

  Число избыточных состояний для любого счетчика определяется из следующего выражения:

М = 2^m - К_сч,

где М - число запрещенных состояний, К_сч - требуемый коэффициент счета; 2^m - число устойчивых состояний двоичного счетчика.

  Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения

n= [log₂ К_сч],

где [log₂ К_сч] - двоичный логарифм заданного коэффициента пересчета К_сч, округленный до ближайшего целого числа.

  В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента пересчета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета К_сч. Один их этих методов заключается в немедленном сбросе в “0” счетчика, установившегося в комбинацию, соответствующему числу К_сч. Его называют также методом автосброса. Рассмотрим пример реализации счетчика с К_сч=10 методом автосброса. Очевидно, что “сбрасывая” двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить”возврат” счетчика в исходное состояние после каждых десяти импульсов. 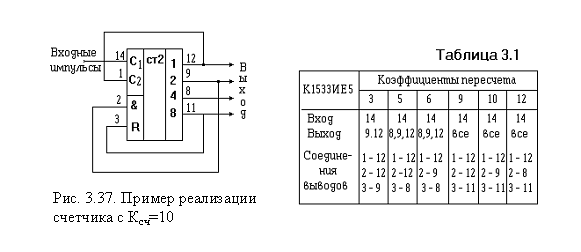Подобный прием удобно применять при использовании счетчиков в интегральном исполнении, имеющих ячейки конъюнкции (И) на входах установки в нуль, как это сделано в микросхеме К1533ИЕ5. В данном примере (рис. 3.37) организованы соединения, обеспечивающие коэффициент пересчета К_сч =10.

  Как следует из рис. 3.37, роль ячейки, выявляющей факт достижения кодовой комбинации 1010 на выходах счетчика, играет ячейка И, уже имеющаяся на входе сброса ИМС К1533ИЕ5.

  В таблице 3.1 поясняются конфигурации соединений для получения различных коэффициентов пересчета с помощью счетчика К1533ИЕ5. Наиболее очевидные варианты получения коэффициентов (2, 4, 8, 16 ) в таблице не указаны. В графе “Соединения” таблицы указано, какие выводы микросхемы должны быть соединены между собой: например, указание 1-12 означает, что нужно соединить вывод 1 с выводом 12. В строках “Ввод” и “Выход” таблицы указаны номера выводов микросхемы, на которые следует подавать входные импульсы и с которых надлежит снимать выходные, соответственно. Следует отметить, что ИМС К1533ИЕ5 состоит из четырех счетных триггеров, один из которых имеет раздельные выводы входа и выхода, а остальные три триггера соединены последовательно по схеме асинхронного счетчика.

  Синтез счетчика с произвольным коэффициентом счета. Один из методов проектирования счетчиков с заданным коэффициентом счета заключается в построении таблицы переходов, в первых столбцах которых будут отражены текущие состояния триггеров счетчика, а в последующих - следующие за ними состояния. Анализ таблицы позволяет установить те переходы, которые должны быть “сделаны” триггерами, входящими в состав счетчика. 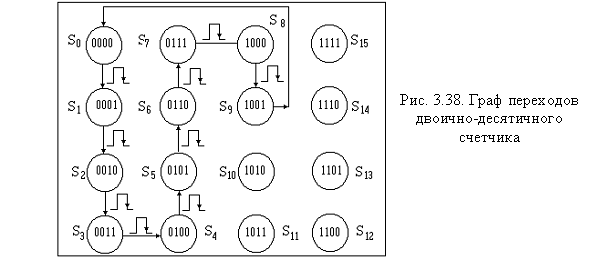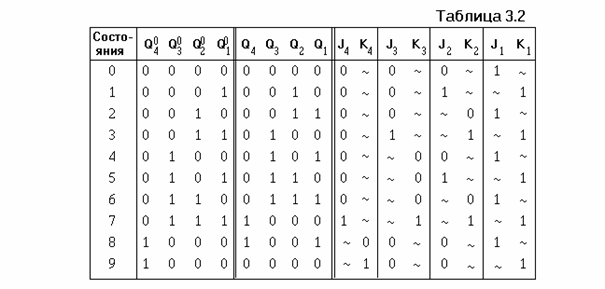Затем с помощью управляющей таблицы соответствующего триггера находятся значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

  Рассмотрим пример синтеза синхронного двоично-десятичного счетчика на базе JK-триггеров. На рис. 3.38 показан граф, поясняющий последовательность переходов десятичного счетчика, в таблице 3.2 - таблица переходов.

  В правой части таблицы 3.2 приведены значения входных сигналов четырех триггеров. Для поиска этих значений должны быть проанализированы реализованные переходы, а затем с помощью управляющей таблицы (см. рис. 3.15, а) определены соответствующие значения “J” и “K” входов триггеров.

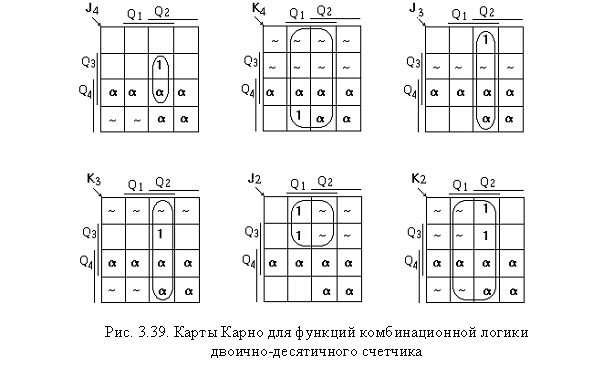
  На рис.3.39 приведены карты Карно для логических функций, которым должны соответствовать сигналы, присутствующие на управ-ляющих входах триггеров ( нулевые значения функций в клетки карты Карно не записаны).

  После упрощения с помощью карт Карно полученные логические выражения, используемые для управления входами “J” и “К”, выглядят

J₄ = Q₁ Q₂ Q₃ ;          K₄ = Q₁

J₃ = Q₁ Q₂;             K₃ = Q₁ Q₂;

J₂ =               K₂ = Q₁

  Просмотр столбцов J₁ и К₁ в табл. 3.2 показывает, что все значения либо “~“, либо “1”. Так как безразличные состояния могут также участвовать в процессе упрощения, то все клетки карты Карно для J₁ и К₁ оказываются заполненными символами “~“, “1” и “a“. Следовательно,

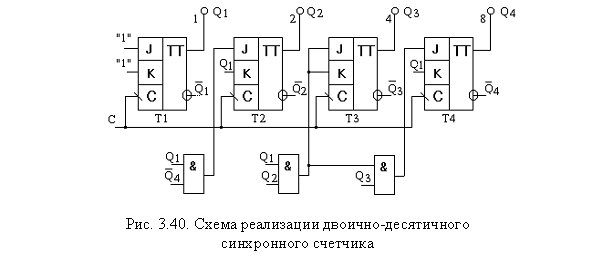
J₁ = K₁ = 1

  На рис. 3.40 показана схема двоично-десятичного синхронного счетчика.

  Если счетчик из-за какой-либо неисправности окажется в одном из запрещенных (неиспользуемых) состояний, то его работа может быть прервана специальным сигналом и также может быть подан сигнал тревоги о неисправности в схеме счетчика. Обнаружить это позволяет схема, реализующая выражение, описывающее функцию неиспользуемых состояний

f_н = Q₂ Q₄ + Q₃ Q₄ .

    На рис. 3.41 показано, как эта схема используется для формирования цепи аварийной сигнализации и генерации блокирующего сигнала синхронизации.

  Выражение , описывающее блокирующий сигнал синхронизации, имеет вид