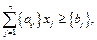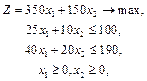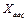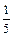Підставимо 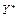 у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
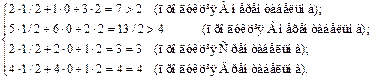
Аналогічні результати можна дістати, проаналізувавши двоїсті оцінки додаткових змінних, значення яких показують, на скільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо  , то відповідна продукція нерентабельна.
, то відповідна продукція нерентабельна.
Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс-таблиці у стовпчиках « » - «
» - « ». їх оптимальні значення
». їх оптимальні значення 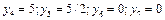 . Тому продукція А і В нерентабельна, а продукція С і Д — рентабельна.
. Тому продукція А і В нерентабельна, а продукція С і Д — рентабельна.
6. Під впливом різних обставин ціна одиниці продукції на підприємстві може змінюватися (збільшуватися чи зменшуватися). І тому завжди цікаво знати, у межах яких змін ціни продукції кожного виду оптимальний план її виробництва залишається таким: 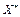 = (0;0;35;45).
= (0;0;35;45).
Для визначення інтервалів зміни коефіцієнтів цільової функції скористаємось тим, що при цьому симплекс-таблиця, яка відповідає оптимальному плану, зберігає свій вигляд за винятком елементів оцінкового рядка. Нові оцінки 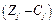 мають задовольняти умову оптимальності задачі максимізації, тобто бути невід'ємними.
мають задовольняти умову оптимальності задачі максимізації, тобто бути невід'ємними.
Зміну коефіцієнта 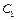 позначимо
позначимо 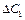 . Оскільки
. Оскільки  — небазисна змінна, то в симплекс-таблиці зміниться лише відповідна оцінка
— небазисна змінна, то в симплекс-таблиці зміниться лише відповідна оцінка  .
.
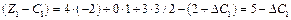 .
.
За умови 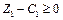 дістанемо нерівність
дістанемо нерівність 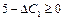 , тобто
, тобто 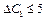 . Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться
. Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться 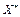 = (0; 0; 35; 45). Лише максимальний дохід зміниться на max
= (0; 0; 35; 45). Лише максимальний дохід зміниться на max 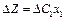 .
.
Аналогічно розраховується інтервал зміни коефіцієнта 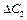 :
:
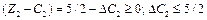
Зі зростанням ціни одиниці продукції В на 5/2 ум. од. за інших однакових умов оптимальний план виробництва продукції не зміниться, а 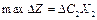 .
.
Дещо складніше розраховується інтервал зміни коефіцієнтів для базисних змінних. У цьому разі зміни відбуваються також у стовпчику «Сбаз» симплекс-таблиці, а це, у свою чергу, стосується всіх ненульових оцінок 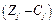 . Так, для базисної змінної х3 зміна коефіцієнта на
. Так, для базисної змінної х3 зміна коефіцієнта на 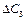 приведе до таких оцінок:
приведе до таких оцінок:

Нові значення оцінок мають задовольняти умову оптимальності, тобто 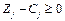 . Тому інтервал для
. Тому інтервал для 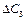 визначається з такої системи нерівностей:
визначається з такої системи нерівностей:
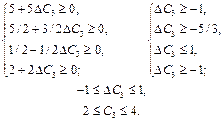
Отже, ціна одиниці продукції С може збільшуватися та зменшуватися на 1 ум. од. і перебувати в межах від 2 до 4 ум. од., але оптимальним планом виробництва продукції залишається 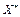 = (0;0;35;45).
= (0;0;35;45).
Для базисної невідомої  інтервал зміни коефіцієнта
інтервал зміни коефіцієнта 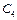 розраховується аналогічно:
розраховується аналогічно:
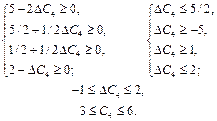
Якщо за інших однакових умов ціна одиниці продукції Д зменшиться до 3 ум. од. або збільшиться до 6 ум. од., то оптимальний план виробництва продукції на підприємстві не зміниться (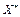 = (0; 0; 35; 45)).
= (0; 0; 35; 45)).
Якщо коливання ціни продукції виходять за визначені межі, то план 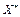 = (0; 0; 35; 45) вже не буде оптимальним і його необхідно буде поліпшити згідно з алгоритмом симплекс-методу, тобто продовжити розв'язування задачі.
= (0; 0; 35; 45) вже не буде оптимальним і його необхідно буде поліпшити згідно з алгоритмом симплекс-методу, тобто продовжити розв'язування задачі.
Виконаний у цій задачі аналіз лінійної моделі на чутливість дає широкий спектр динамічної інформації про визначений оптимальний план і дає змогу дослідити можливі зміни цього оптимального плану в результаті коректування умов прямої задачі.
4.3. Аналіз цільової функції і коефіцієнтів технологічної матриці. Приклади:
Фірма виготовляє продукцію трьох видів А, В і С. Для цього потрібний певний час обробки кожної продукції на різних групах обладнання (1, 2, 3) (див. таблицю).
| Ресурс
| Час обробки продукції, год, за видами
|
| А
| В
| С
|
|
|
|
|
|
Можливий час роботи обладнання кожного типу становить відповідно 360, 520 та 220 год на місяць. Ціна одиниці продукції А дорівнює 90 дол., продукції В — 110дол., а продукції С — 150 дол. Визначити, яку продукцію і в якій кількості слід виготовляти, щоб фірма отримувала найбільший дохід.
Розв'язування задачі симплекс-методом дає таку останню симплексну таблицю:
| Базис
| 
| План
|
|
|
|
|
|
|

| 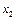
| 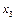
| 
| 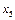
| 
|

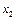

|
|
|
|
|
-1
|
| -1/2
1/2
-1/2
|
-1
|
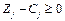
| 20 600
|
|
|
|
|
|
|
Керівництво фірми цікавить, чи зміниться оптимальний план виробництва продукції і якщо зміниться, то яким буде новий оптимальний план у кожній з наведених далі ситуацій.
1. Фірма може збільшити час роботи обладнання груп 2 та 3 відповідно на 100 та 80 год за місяць, орендуючи для цього додаткове обладнання, яке коштуватиме 5000 дол. Чи вигідно це? Якщо вигідно, то яким має бути новий план виробництва продукції?
2. Фінансовий відділ фірми вважає, що загострення конкуренції на ринку збуту може призвести до зниження ціни на продукцію В на 25 дол. Як це позначиться на оптимальному плані виробництва продукції фірми?
Відділ досліджень і розробок фірми пропонує виготовляти дешевшу модифікацію продукції С. Для виробництва одиниці цієї нової продукції потрібний час роботи обладнання груп 1, 2 та 3 становить відповідно 4, 3 та 1 год. Орієнтовна ціна одиниці нової продукції дорівнює 120 дол. Керівництво фірми цікавить, чи буде за таких умов виробництво нової продукції вигідним.
Споживач продукції А за певних обставин порушує попере дню домовленість і відмовляється прийняти більш як 100 од. продукції А. Визначити, як фірма має змінити план виробництва своєї продукції, щоб уникнути втрат, пов'язаних із надвиробництвом відповідного виду продукції.
Розв'язування. Із наведеної в умові задачі симплекс-таблиці маємо: 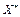 = (180; 40; 0; 100; 0; 0),
= (180; 40; 0; 100; 0; 0), 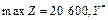 = (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції А та 40 од. продукції В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальний дохід у розмірі 20 600 дол. на місяць.
= (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції А та 40 од. продукції В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальний дохід у розмірі 20 600 дол. на місяць.
1. Збільшення часу роботи обладнання дасть змогу збільшити випуск продукції, тобто змінить оптимальний план і дохід фірми. Оскільки 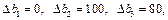 новий оптимальний план визначається так:
новий оптимальний план визначається так:
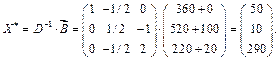
Новий план допустимий (всі 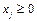 ), і тому оптимальні двоїсті оцінки зберігають свої значення:
), і тому оптимальні двоїсті оцінки зберігають свої значення: 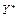 = (0; 10; 70). Приріст доходу фірми в результаті зміни оптимального плану виробництва продукції розраховується так:
= (0; 10; 70). Приріст доходу фірми в результаті зміни оптимального плану виробництва продукції розраховується так:
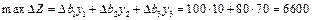 дол.
дол.
Оскільки дохід фірми від додаткового використання обладнання груп 2 і 3 перевищує витрати на оренду цього обладнання (6600 > 5000), то природно, що така тактика фірми буде вигідною. При цьому оптимальним планом виробництва стане випуск 290 од. продукції А і 10 од. продукції В. Невикористаний час роботи обладнання групи 1 зменшиться до 50 год на місяць, а дохід фірми за відрахуванням витрат на оренду обладнання дорівнюватиме 20 600 + (6600 - 5000) = 22 200 дол. на місяць.
2. Зміна ціни одиниці продукції В на 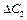 (25 дол.) стосується всього оцінкового рядка симплекс-таблиці, оскільки х2 є базисною змінною. Нові
(25 дол.) стосується всього оцінкового рядка симплекс-таблиці, оскільки х2 є базисною змінною. Нові 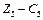 матимуть такі значення:
матимуть такі значення:
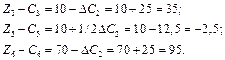
Коли б усі здобуті оцінки задовольняли умову Z5 – С5 ≥ 0, то це означало б, що попри зниження ціни план виробництва продукції на фірмі не зміниться. Але оцінка 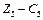 не задовольняє умову оптимальності задачі на максимум, і тому можна зробити такий висновок. Істотне зниження ціни одиниці продукції В порушує визначений раніше оптимальний план виробництва продукції, оскільки випуск продукції виду В стає для фірми невигідним, нерентабельним.
не задовольняє умову оптимальності задачі на максимум, і тому можна зробити такий висновок. Істотне зниження ціни одиниці продукції В порушує визначений раніше оптимальний план виробництва продукції, оскільки випуск продукції виду В стає для фірми невигідним, нерентабельним.
Новий оптимальний план визначається у процесі подальшого розв'язування задачі симплекс-методом:
| Базис
| 
| План
|
|
|
|
|
|
| q
|

| 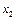
| 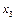
| 
| 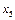
| 
|

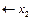

|
|
|
|
|
-1
|
| -1/2
 -1/2
-1/2
|
-1
| -
-
|
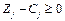
| 19 600
|
|
|
|
| -2,5
|
|
|

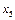

|
|
|
|
|
-2
|
|
| -1
-2
|
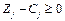
| 19 800
|
|
|
|
|
|
|
Отже, у розглянутій ситуації зниження ціни одиниці продукції виду В на 25 дол. різко змінить структуру та обсяги виробництва продукції на фірмі. Вигідним стане випуск лише продукції А у кількості 220 од.: при цьому час роботи обладнання груп 1 і 2 використовуватиметься повністю. Усе це призведе до зменшення доходу фірми до 19 800 дол. на місяць.
3. Обсяг виробництва нової продукції в оптимальному плані позначимо  . Тоді математична модель прямої задачі матиме такий вигляд:
. Тоді математична модель прямої задачі матиме такий вигляд:

У математичній моделі двоїстої задачі змінній  відповідатиме таке обмеження:
відповідатиме таке обмеження: 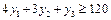 . Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок:
. Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок: 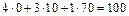 , що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього
, що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього  .
.
Для цього за допомогою оберненої матриці необхідно визначити елементи стовпчика « » останньої симплекс-таблиці:
» останньої симплекс-таблиці:
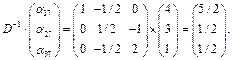
Результати однієї ітерації симплекс-методу, що приводить до нового оптимального плану задачі, наведено далі.
| Базис
| 
| План
|
|
|
|
|
|
|
| q
|

| 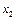
| 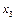
| 
| 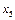
| 
| 
|
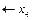

|
|
|
|
|
-1
|
| -1/2
1/2
-1/2
|
-1
|   1/2
1/2
1/2
1/2
|
|
| 20 600
|
|
|
|
|
|
| -20
|
|


|
|
|
|
| 6/5
-8/5
12/5
| 2/5
-1/5
-1/5
| -1/5
3/5
-2/5
|
-1
|
|
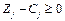
| 21 400
|
|
|
|
|
|
|
|
Як бачимо з таблиці, 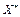 = (160; 20; 0; 0; 0; 0; 40),
= (160; 20; 0; 0; 0; 0; 40), 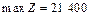 . Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною, виготовляючи її в кількості 40 од.; відповідно продукції А — 160 од. і продукції В — 20 од. Такий новий оптимальний план виробництва продукції збільшить дохід фірми до 21 400 дол. на місяць.
. Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною, виготовляючи її в кількості 40 од.; відповідно продукції А — 160 од. і продукції В — 20 од. Такий новий оптимальний план виробництва продукції збільшить дохід фірми до 21 400 дол. на місяць.
4. Четверта запропонована ситуація математично пов'язана з уведенням в умову задачі додаткового обмеження, що може при вести до таких наслідків:
а) нове обмеження для визначеного оптимального плану виконується і тоді воно є надлишковим, зайвим і його включення до моделі не змінює визначеного плану;
б) нове обмеження для визначеного оптимального плану не виконується, і тоді за допомогою двоїстого симплекс-методу не обхідно знайти новий оптимальний план.
За умовою задач додатковим є обмеження 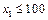 . Але воно суперечить оптимальній кількості продукції А, яка дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв'язування задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду:
. Але воно суперечить оптимальній кількості продукції А, яка дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв'язування задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду:
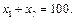
Оскільки в оптимальному плані змінна х1є базисною, її необхідно записати через небазисні невідомі. Це робиться так. У симплекс-таблиці, яку наведено в умові задачі, рядок змінної “х1” подається рівнянням

З цього рівняння визначимо  :
:
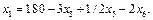
Підставивши цей вираз в додаткове обмеження, отримаємо
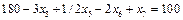
або
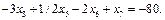
У такому вигляді додаткове обмеження дописується в симплекс-таблицю. Застосування двоїстого симплекс-методу приведе до нового оптимального плану задачі:
| Базис
| 
| План
|
|
|
|
|
|
|
|

| 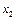
| 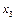
| 
| 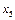
| 
| 
|

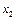

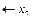
|
|
-80
|
|
|
-1
 
|
| -1/2
1/2
-1/2
1/2
|
-1
-2
|
|
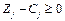
| 20 600
|
|
|
|
|
|
|
|

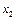

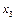
|
|
200/3
80/3
|
|
|
|
|
1/3
-1/6
| -2
-1/3
2/3
|
-1/3
-1/3
|
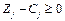
| 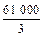
|
|
|
|
| 35/3
| 190/3
| 10/3
|
З останньої таблиці маємо 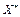 = (100; 200/3; 80/3; 20; 0;0),
= (100; 200/3; 80/3; 20; 0;0), 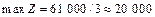 .
.
Проаналізуємо цей план. Реалізація запропонованої в умові задачі ситуації змінює структуру та кількісний вираз оптимального плану. Тепер з урахуванням вимог споживача фірма виготовлятиме 100 од. продукції А, 200/3 од. продукції В і 80/3 од. продукції С. У результаті такого плану випуску продукції дохід фірми зменшиться до 20 333 дол. на місяць.
ТЕМА 5
ТРАНСПОРТНА ЗАДАЧА. ПОСТАНОВКА, МЕТОДИ РОЗВ’ЯЗУВАННЯ ТА АНАЛІЗУ.
5.1. Економічна і математична постановка ТЗ. Умови існування розв’язку ТЗ.
Транспортна задача — це специфічна задача лінійного програмування, застосовувана для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів.
Математична модель транспортної задачі має такий вигляд:
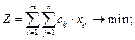
| (5.1)
|
за обмежень
де  — кількість продукції, що перевозиться від і-го постачальника до j-го споживача;
— кількість продукції, що перевозиться від і-го постачальника до j-го споживача; 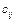 — вартість перевезення одиниці продукції від i-го постачальника до j-го споживача;
— вартість перевезення одиниці продукції від i-го постачальника до j-го споживача; 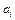 — запаси продукції i-го постачальника;
— запаси продукції i-го постачальника; 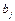 — попит на продукцію j-го споживача.
— попит на продукцію j-го споживача.
Якщо в транспортній задачі загальна кількість продукції постачальників дорівнює загальному попиту всіх споживачів, тобто
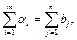
| (5.5)
|
то таку транспорту задачу називають збалансованою, або закритою. Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою.
Планомтранспортної задачі називають будь-який невід'ємний розв'язок системи обмежень (5.2)—(5.4) транспортної задачі, який позначають матрицею 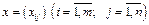 .
.
Оптимальним планомтранспортної задачі називають матрицю 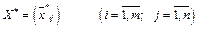 , яка задовольняє умови задачі і для якої цільова функція (5.1) набуває найменшого значення.
, яка задовольняє умови задачі і для якої цільова функція (5.1) набуває найменшого значення.
! Теорема (умова існування розв'язку транспортної задачі). Необхідною і достатньою умовою існування розв'язку транспортної задачі є її збалансованість, тобто 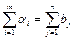 .
.
5.2. Методи побудови опорного плану. Впровадження. Двоїстість.
Транспортна задача є задачею лінійного програмування, яку можна розв'язати симплекс-методом. Але специфічна структура транспортної задачі дає змогу використовувати для її розв'язування ефективніший метод, який повторює, по суті, кроки симплекс-алгоритму. Таким є метод потенціалів.
Алгоритм методу потенціалів складається з таких етапів.
Визначення типу транспортної задачі (відкрита чи закрита).
Побудова першого опорного плану транспортної задачі.
Перевірка плану транспортної задачі на оптимальність.
Якщо умова оптимальності виконується, то маємо оптимальний розв'язок транспортної задачі. Якщо ж умова оптимальності не виконується, необхідно перейти до наступного опорного плану.
Новий план знову перевіряють на оптимальність, тобто повторюють дії п. 3, і т. д.
Розглянемо докладно кожний етап цього алгоритму.
1. Якщо під час перевірки збалансованості (5.5) виявилося, що транспортна задача є відкритою, то її необхідно звести до закритого типу. Це виконується введенням фіктивного умовного постачальника 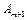 у разі перевищення загального попиту над запасами
у разі перевищення загального попиту над запасами 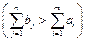 із запасом
із запасом 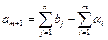 . Якщо ж загальні запаси постачальників перевищують попит споживачів
. Якщо ж загальні запаси постачальників перевищують попит споживачів 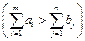 до закритого типу задача зводиться введенням фіктивного умовного споживача
до закритого типу задача зводиться введенням фіктивного умовного споживача 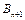 з потребою
з потребою 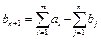 .
.
Вартість перевезення одиниці продукції для фіктивного постачальника 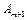 , або фіктивного споживача
, або фіктивного споживача 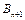 . вважається такою, що дорівнює нулю.
. вважається такою, що дорівнює нулю.
2. Для побудови початкового опорного плану транспортної задачі існує кілька методів: північно-західного кута; мінімальної вартості; подвійної переваги; апроксимації Фогеля. Побудову опорного плану зручно подавати у вигляді таблиці, в якій постачальники продукції є рядками, а споживачі — стовпчиками.
Побудову першого плану за методом північно-західного кута починають із заповнення лівої верхньої клітинки таблиці (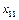 ), в яку записують менше з двох чисел
), в яку записують менше з двох чисел 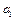 та
та 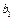 . Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.
. Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.
Ідея методу мінімальної вартості полягає в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції. Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.
Метод подвійної переваги. Перед початком заповнення таблиці необхідно позначити клітинки, які мають найменшу вартість у рядках і стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (як мінімальні і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (як мінімальні або в рядку, або в стовпчику), а вже потім — за методом мінімальної вартості.
Метод апроксимації Фогеля. За цим методом на кожному кроці визначають різницю між двома найменшими вартостями в кожному рядку і стовпчику транспортної таблиці. Ці різниці записують у спеціально відведених місцях таблиці. Серед усіх різниць вибирають найбільшу і у відповідному рядку чи стовпчику заповнюють клітинку з найменшою вартістю. Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпчик. Коли залишається незаповненим лише один рядок або стовпчик, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості.
Після побудови першого опорного плану одним із розгляну тих методів у таблиці має бути заповнено (т + п - 1) клітинок, де т — кількість постачальників; п — кількість споживачів у задачі, утому числі фіктивних. Такий план називають не виродженим. Якщо кількість заповнених клітинок перевищує (m + n - 1), то початковий план побудовано неправильно і він є неопорним. Ознакою опорності плану транспортної задачі є його ациклічність, тобто неможливість побудови циклу. Циклому транспортній задачі називають замкнену ламану лінію, вершини якої розміщуються в заповнених клітинках таблиці, а сторони проходять уздовж рядків і стовпчиків таблиці.
Якщо заповнених клітинок у таблиці менш як (т + п - 1), то опорний план називають виродженим. У такому разі необхідно заповнити відповідну кількість порожніх клітинок, записуючи в них «нульове перевезення», але так, щоб при цьому не порушилася ациклічність плану.
3. Опорний план перевіряють на оптимальність за допомогою потенціалів ui та vj відповідно постачальників та споживачів.
! Теорема (умова оптимальності опорного плану транспортної задачі). Якщо для деякого опорного плану 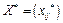 існують числа
існують числа 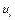 та
та 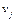 , для яких виконується умова
, для яких виконується умова 
для всіх 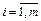 , та
, та 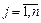 , то він є оптимальним планом транспортної задачі.
, то він є оптимальним планом транспортної задачі.
Потенціали опорного плану визначаються із системи рівнянь  , які записують для всіх заповнених клітинок транспортної таблиці.
, які записують для всіх заповнених клітинок транспортної таблиці.
4. За допомогою розрахованих потенціалів перевіряють умову оптимальності  для порожніх клітинок таблиці. Якщо хоча б для однієї клітинки ця умова нєвиконується, тобто
для порожніх клітинок таблиці. Якщо хоча б для однієї клітинки ця умова нєвиконується, тобто 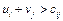 , поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.
, поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.
Перехід від одного опорного плану до іншого виконують заповненням клітинки, для якої порушено умову оптимальності. Якщо таких клітинок кілька, то для заповнення вибирають таку, що має найбільше порушення, тобто 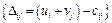 . Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:
. Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:
1) кожній вершині циклу приписують певний знак, причому вільній клітинці — знак «+», а всім іншим по черзі — знаки «-» та «+»;
2) у порожню клітинку переносять менше з чисел хij, що стоять у клітинках зі знаком «-». Одночасно це число додають до відповідних чисел, які розміщуються в клітинках зі знаком «+».
Отже, клітинка, що була вільною, стає заповненою, а відповідна клітинка з мінімальним числом  вважається порожньою. У результаті такого перерозподілу продукції дістанемо новий опорний план транспортної задачі.
вважається порожньою. У результаті такого перерозподілу продукції дістанемо новий опорний план транспортної задачі.
Новий опорний план перевіряють на оптимальність згідно з п. 3 розглянутого алгоритму.
Розглянемо застосування методу потенціалів для розв'язування транспортних задач, наведених далі.
5.3. ТЗ за критерієм часу. Двостапна ТЗ. Розв’язання по сітці.
Компанія контролює три фабрики 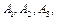 здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками
здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками 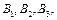 яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.
яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.
| Фабрика
| Вартість виробництва і транспортування
1000 од. продукції за замовниками
|
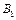
| 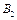
| 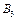
| 
|
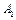
|
|
|
|
|
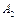
|
|
|
|
|

|
|
|
|
|
Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.
Побудова математичної моделі. Нехай  — кількість продукції, що перевозиться з і-ї фабрики до j-го замовника
— кількість продукції, що перевозиться з і-ї фабрики до j-го замовника 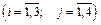 . Оскільки транспортна задача за умовою є збалансованою, закритою
. Оскільки транспортна задача за умовою є збалансованою, закритою 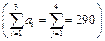 , то математична модель задачі матиме вигляд
, то математична модель задачі матиме вигляд
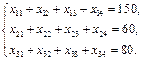
Економічний зміст записаних обмежень полягає ось у чому: уся вироблена на фабриках продукція має вивозитися до замовників повністю.
Аналогічні обмеження можна записати відносно замовників: продукція, що надходить до споживача, має повністю задовольняти його попит. Математично це записується так:
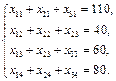
Загальні витрати, пов'язані з виробництвом і транспортуванням продукції, складаються як добуток обсягу перевезеної продукції та питомої вартості перевезень за відповідним маршрутом і за умовою задачі мають бути мінімальними. Тому
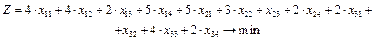
У цілому математичну модель поставленої задачі можна записати так:

Розв'язування. Розв'язування задачі подамо в таблицях, які назвемо транспортними. Перший опорний план задачі побудуємо методом мінімальної вартості.
Тому 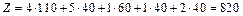 ум. од.
ум. од.
Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п'яти, а (m + n - 1) = 3 + 4 - 1= 6. Для подальшого розв'язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зайняти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку 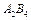 . Тепер перший план транспортної задачі є не виродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.
. Тепер перший план транспортної задачі є не виродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.
На основі першої умови оптимальності  складемо систему рівнянь для визначення потенціалів плану:
складемо систему рівнянь для визначення потенціалів плану:
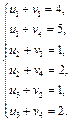
Записана система рівнянь є невизначеною, і один з її розв'язків дістанемо, якщо, наприклад, 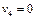 . Тоді всі інші потенціали однозначно визначаються:
. Тоді всі інші потенціали однозначно визначаються: 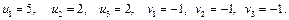 .
.
Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності 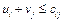 (для порожніх клітинок таблиці):
(для порожніх клітинок таблиці):

Умова оптимальності не виконується для клітинки 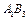 . Порушення
. Порушення  записуємо в лівому нижньому кутку відповідної клітинки.
записуємо в лівому нижньому кутку відповідної клітинки.
Перший опорний план транспортної задачі є неоптимальним. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці.
Потрібно заповнити клітинку 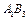 , в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки
, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки 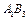 , та позначаємо вершини циклу почергово знаками «-» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку
, та позначаємо вершини циклу почергово знаками «-» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку 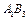 переносимо менше з чисел
переносимо менше з чисел  , які розміщуються в клітинках зі знаком «-». Одночасно це саме число
, які розміщуються в клітинках зі знаком «-». Одночасно це саме число  додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «-».
додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «-».
У даному випадку 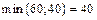 , тобто
, тобто 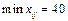 . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка
. Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка 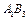 — 40 од. продукції,
— 40 од. продукції,  од.,
од., 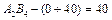 од. Клітинка
од. Клітинка 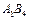 , звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (п + т- 1).
, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (п + т- 1).
Отже, другий опорний план транспортної задачі матиме такий вигляд:
Тому 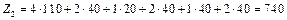 ум. од.
ум. од.
Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий план транспортної задачі також неоптимальний (порушення для клітинки 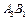 ). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю:
). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю:
Тому 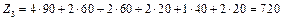 ум. од.
ум. од.
Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому
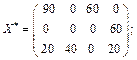
За оптимальним планом перевезень перший замовник отримує 90 тис. од. продукції з першої фабрики та 20 тис. од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис. од. продукції з третьої фабрики і т. д. При цьому загальна вартість виробництва та перевезення всієї продукції є найменшою і становить 720 ум. од.
ТЕМА 6.
ЦІЛОЧИСЛОВІ ЗАДАЧІ ЛІНІЙНОГО ПРОГРАМУВАННЯ. ОСНОВНІ МЕТОДИ ЇХ РОЗВ’ЯЗУВАННЯ ТА АНАЛІЗУ.
6.1. Область застосування ЦЗЛП.
У попередніх розділах було розглянуто задачі лінійного програмування та методи їх розв'язування. Ці методи найбільш розроблені, легко реалізуються на ПЕОМ, а тому набули широкого застосування в багатьох галузях науки, техніки та економіки. Проте лінійні моделі відбивають лише певну й вельми обмежену сукупність властивостей навколишнього світу. Адже, скажімо, соціально-економічні процеси не є лінійними. Галузі, об'єднання та окремі підприємства народного господарства функціонують і розвиваються за умов невизначено сті, а тому описуються нелінійними, стохастичними, динамічними процесами. Отже, для управління народним господарством, його галузями й тими чи іншими об'єктами господарювання потрібні нелінійні економіко-математичні моделі та методи. А вони ще недостатньо розроблені і до того ж не так легко, як лінійні, піддаються реалізації на ПЕОМ. Щоправда, нелінійні, стохастичні задачі нерідко вдається звести до лінійних, а далі — скористатися відповідними добре розробленими методами розв'язування. Однак такий підхід щоразу потребує певних застережень.
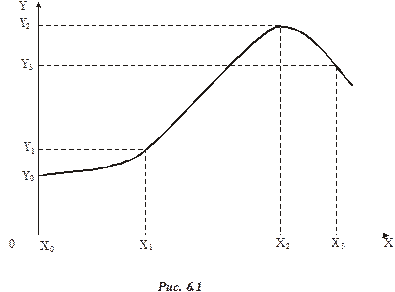 Розглянемо приклад. Урожайність сільськогосподарських культур залежить, як відомо, від багатьох чинників, серед яких насамперед слід назвати заходи з підживлення ґрунту. Природна родючість земельних угідь забезпечує лише певний рівень продуктивності рослин. Щоб підвищити їх урожайність, використовують органічні та мінеральні добрива. Залежність урожайності цукрових буряків від кількості внесених мінеральних добрив ілюструє рис. 6.1.
Розглянемо приклад. Урожайність сільськогосподарських культур залежить, як відомо, від багатьох чинників, серед яких насамперед слід назвати заходи з підживлення ґрунту. Природна родючість земельних угідь забезпечує лише певний рівень продуктивності рослин. Щоб підвищити їх урожайність, використовують органічні та мінеральні добрива. Залежність урожайності цукрових буряків від кількості внесених мінеральних добрив ілюструє рис. 6.1.
Із рис. 6.1 бачимо, що за рахунок природної родючості ґрунту та внесення органічних добрив досягається врожайність цукрових буряків 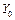 . Зі зростанням кількості внесених мінеральних добрив урожайність цієї культури підвищується. Наприклад, якщо ця кількість збільшується від
. Зі зростанням кількості внесених мінеральних добрив урожайність цієї культури підвищується. Наприклад, якщо ця кількість збільшується від 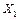 до
до 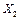 (реально це 100—280 кг діючої речовини на гектар), то врожайність цукрових буряків зростає майже лінійно, приблизно від 150 до 450 ц/га. Проте з подальшим збільшенням кількості внесених мінеральних добрив
(реально це 100—280 кг діючої речовини на гектар), то врожайність цукрових буряків зростає майже лінійно, приблизно від 150 до 450 ц/га. Проте з подальшим збільшенням кількості внесених мінеральних добрив 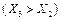 урожайність знижується
урожайність знижується 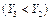 , оскільки рослини не забезпечуються іншими необхідними елементами, наприклад водою.
, оскільки рослини не забезпечуються іншими необхідними елементами, наприклад водою.
Отже, якщо в розробленій економіко-математичній моделі вирощування цукрових буряків взяти обмеження за рівнем їх урожайності (скажімо, 150—450 ц/га), то з відповідними застереженнями можна припустити, що існує лінійна залежність між урожайністю цукрового буряку та обсягами внесених і органічних добрив.
Зауважимо, що розвиток комп'ютерної техніки і методів математичного моделювання створює передумови для використання нелінійних методів, а це може значною мірою підвищити якість розроблюваних планів, надійність та ефективність прийнятих рішень. У цьому розділі стисло розглянемо деякі методи математичного програмування, що вкрай потрібні економістові XXI століття. Докладніше ці питання розглядаються в [5; 10; 15; 16; 26; 34; 35].
Зауважимо, що фахівець, який розробив економіко-математичну модель, але через її складність не реалізував на ПЕОМ, істотно поповнив свої знання про досліджуваний процес, а отже, і прийняті ним (свідомо чи несвідомо) рішення є більшобґрунто ваними й економічно ефективними, ніж ті, які могли б постати без вивчення зазначеної моделі.
6.2. Математична постановка ЦЗЛП.Геометрична інтерпретація розв’язків на площині.
Існує доволі широкий клас задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень, наприклад, коли йдеться про кількість верстатів у цеху, корів у сільськогосподарських підприємствах тощо, тобто коли така вимога випливає з особливостей технології виробництва. До цілочислового програмування належать також задачі оптимізації, в яких змінні набувають лише двох значень — 0 або 1 (бульові, або бінарні, змінні).
Розглянемо приклад. Інвестиційна компанія може вкласти кошти у три різні підприємства. Ефективність кожного проекту оцінено згідно з тим, що його реалізація можлива за чотирьох умов. Дані про ці проекти наведено в таблиці:
| Проект
| Змінна
| Умови реалізації проектів
|
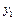
| 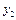
| 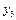
| 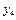
|
|
| 
|
|
|
|
|
|
| 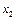
|
|
|
|
|
|
| 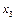
|
|
|
|
|
| Імовірності оцінки реалізації проектів
| 0,2
| 0,1
| 0,4
| 0,3
|
Кожна змінна 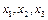 може набувати лише двох значень -1 або 0, тобто інвестиційна компанія вкладає або не вкладає кошти у відповідне підприємство.
може набувати лише двох значень -1 або 0, тобто інвестиційна компанія вкладає або не вкладає кошти у відповідне підприємство.
До цілочислового програмування відносять задачі про призначення, найкоротший шлях і т. ін. У реальних задачах часто цілочислових значень набувають не всі, а одна чи кілька змінних. Такі задачі називають частково цілочисловими.
Загальна задача цілочислового програмування записується так:
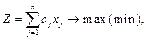
| (6.1)
|
за умов
Для знаходження оптимального розв'язку цілочислових задач застосовують спеціальні методи. Найпростішим методом розв'язування цілочислової задачі є знаходження її оптимального розв'язку як задачі, що має лише неперервні змінні, з подальшим округленням останніх. Такий підхід часто є виправданим. Нехай, наприклад, у результаті розв'язування задачі про поєднання галузей у сільськогосподарському підприємстві дістали, що воно по требує 1235,6 корів. Округливши це значення корів до 1236, не припустимося значної похибки. Проте в деяких випадках такі спрощення призводять до істотних неточностей. Якщо, скажімо, у разі розв'язування як неперервної задачі про сушильний цех, що може бути обладнаний агрегатами трьох типів, дістали 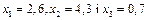 , будь-які округлення недопустимі.
, будь-які округлення недопустимі.
Для знаходження оптимальних планів задач цілочислового програмування застосовують дві основні групи методів:
· методи відтинання;
· комбінаторні методи.
Основою методів відтинання є ідея поступового «звуження» області допустимих розв'язків розглядуваної задачі. Пошук ціло числового оптимуму починається з розв'язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, многокутник допустимих розв'язків послабленої задачі поступово зменшуємо доти, доки змінні оптимального розв'язку не набудуть цілочислових значень.
До цієї групи належать:
а) методи розв'язування повністю цілочислових задач (дробовий алгоритм Гоморі);
б) методи розв'язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
Комбінаторні методи цілочислової оптимізації базуються на повному переборі всіх допустимих цілочислових розв'язків, тобто вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається лише частина розв'язків (досить невелика), а решта враховується одним зі спеціальних методів.
Найпоширенішим у цій групі методів є метод віток і меж.
Починаючи з розв'язування послабленої задачі, він передбачає розбиття початкової задачі на дві підзадачі виключенням областей, що не мають цілочислових розв'язків, і дослідженням кожної окремої частини многокутника допустимих розв'язків.
Для розв'язування задач із бульовими змінними застосовують комбіновані методи, причому оскільки змінні є бульовими, то методи пошуку оптимуму значно спрощуються.
6.3. Метод Гоморі
Нехай маємо задачу цілочислового програмування (6.1)— (6.4). Для її розв'язування можна скористатися ітеративним методом Гоморі. Суть його полягає ось у чому:
1. Знаходять розв'язок послабленої, тобто задачі без вимог цілочисловості змінних — (6.1)—(6.3).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування (6.1)—(6.4).
2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
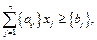
де символ {} позначає дробову частину числа.
Для визначення дробової частини будь-якого числа від цього числа віднімають цілу його частину — найбільше ціле число, що не перевищує даного. Цілу частину числа позначають символом []. Наприклад,
[1,3] = 1; [-1,3] = -2; {1,3} = 1,3 - 1 = 0,3; {-1,3} = -1,3 - (-2) =2 - 1,3 = 0,7.
Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Здобуту розширену задачу розв'язують, а далі перевіряють її розв'язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв'язку або доведено, що задача не має допустимих розв'язків у множині цілих чисел.
Досвід показує, що процес розв'язування задач великої розмірності методом Гоморі повільно збіжний. Істотними є також похибки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.
Задача 6.1.Сільськогосподарське підприємство задумало створити сушильний цех на виробничій площі 190м2, маючи для цього 100 тис.грн. і можливість придбати устаткування двох типів А і В. Техніко-економічну інформацію про ці два види устаткування подано в таблиці:
| Техніко-економічний показник
| Устаткування
| Ресурс
|
| А
| В
|
| Вартість, тис. грн.
|
|
|
|
| Необхідна виробнича площа, м2
|
|
|
|
| Потужність, тис. грн./рік
|
|
| -
|
Розв'язування. Нехай  і
і 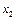 — кількість комплектів устатку вання відповідно типу А і В.
— кількість комплектів устатку вання відповідно типу А і В.
Запишемо економіко-математичну модель:
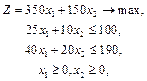
 і
і 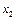 - цілі.
- цілі.
Розв'язуємо задачу, нехтуючи умовою цілочисловості. Остання симплексна таблиця набере вигляду:


 у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.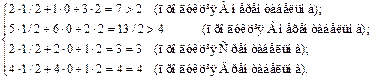
 , то відповідна продукція нерентабельна.
, то відповідна продукція нерентабельна. » - «
» - « ». їх оптимальні значення
». їх оптимальні значення 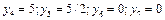 . Тому продукція А і В нерентабельна, а продукція С і Д — рентабельна.
. Тому продукція А і В нерентабельна, а продукція С і Д — рентабельна.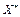 = (0;0;35;45).
= (0;0;35;45).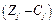 мають задовольняти умову оптимальності задачі максимізації, тобто бути невід'ємними.
мають задовольняти умову оптимальності задачі максимізації, тобто бути невід'ємними.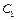 позначимо
позначимо 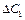 . Оскільки
. Оскільки  .
.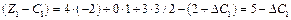 .
.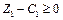 дістанемо нерівність
дістанемо нерівність 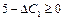 , тобто
, тобто 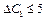 . Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться
. Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться 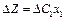 .
.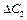 :
: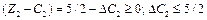
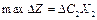 .
.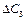 приведе до таких оцінок:
приведе до таких оцінок:
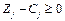 . Тому інтервал для
. Тому інтервал для 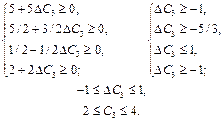
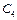 розраховується аналогічно:
розраховується аналогічно: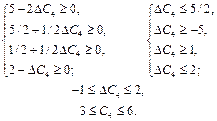


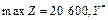 = (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції А та 40 од. продукції В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальний дохід у розмірі 20 600 дол. на місяць.
= (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції А та 40 од. продукції В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальний дохід у розмірі 20 600 дол. на місяць.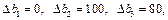 новий оптимальний план визначається так:
новий оптимальний план визначається так: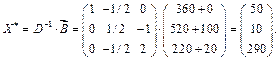
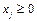 ), і тому оптимальні двоїсті оцінки зберігають свої значення:
), і тому оптимальні двоїсті оцінки зберігають свої значення: 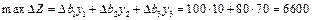 дол.
дол.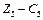 матимуть такі значення:
матимуть такі значення: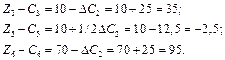
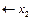
 -1/2
-1/2
 . Тоді математична модель прямої задачі матиме такий вигляд:
. Тоді математична модель прямої задачі матиме такий вигляд:
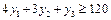 . Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок:
. Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок: 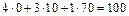 , що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього
, що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього 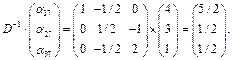
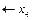
 1/2
1/2
1/2
1/2
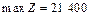 . Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною, виготовляючи її в кількості 40 од.; відповідно продукції А — 160 од. і продукції В — 20 од. Такий новий оптимальний план виробництва продукції збільшить дохід фірми до 21 400 дол. на місяць.
. Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною, виготовляючи її в кількості 40 од.; відповідно продукції А — 160 од. і продукції В — 20 од. Такий новий оптимальний план виробництва продукції збільшить дохід фірми до 21 400 дол. на місяць.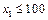 . Але воно суперечить оптимальній кількості продукції А, яка дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв'язування задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду:
. Але воно суперечить оптимальній кількості продукції А, яка дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв'язування задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду: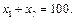

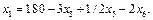
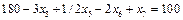
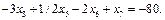
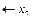


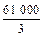
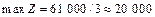 .
.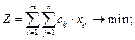
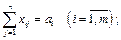
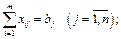
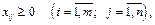
 — кількість продукції, що перевозиться від і-го постачальника до j-го споживача;
— кількість продукції, що перевозиться від і-го постачальника до j-го споживача; 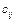 — вартість перевезення одиниці продукції від i-го постачальника до j-го споживача;
— вартість перевезення одиниці продукції від i-го постачальника до j-го споживача; 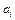 — запаси продукції i-го постачальника;
— запаси продукції i-го постачальника; 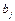 — попит на продукцію j-го споживача.
— попит на продукцію j-го споживача.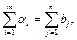
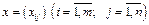 .
.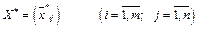 , яка задовольняє умови задачі і для якої цільова функція (5.1) набуває найменшого значення.
, яка задовольняє умови задачі і для якої цільова функція (5.1) набуває найменшого значення.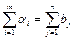 .
.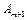 у разі перевищення загального попиту над запасами
у разі перевищення загального попиту над запасами 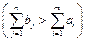 із запасом
із запасом 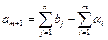 . Якщо ж загальні запаси постачальників перевищують попит споживачів
. Якщо ж загальні запаси постачальників перевищують попит споживачів 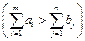 до закритого типу задача зводиться введенням фіктивного умовного споживача
до закритого типу задача зводиться введенням фіктивного умовного споживача 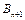 з потребою
з потребою 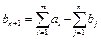 .
.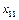 ), в яку записують менше з двох чисел
), в яку записують менше з двох чисел 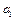 та
та 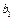 . Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.
. Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.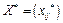 існують числа
існують числа 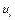 та
та 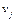 , для яких виконується умова
, для яких виконується умова 
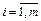 , та
, та 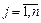 , то він є оптимальним планом транспортної задачі.
, то він є оптимальним планом транспортної задачі. , які записують для всіх заповнених клітинок транспортної таблиці.
, які записують для всіх заповнених клітинок транспортної таблиці.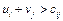 , поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.
, поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.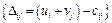 . Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:
. Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами: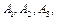 здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками
здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками 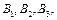 яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.
яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.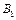
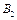
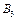

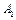
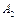

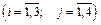 . Оскільки транспортна задача за умовою є збалансованою, закритою
. Оскільки транспортна задача за умовою є збалансованою, закритою 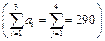 , то математична модель задачі матиме вигляд
, то математична модель задачі матиме вигляд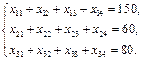
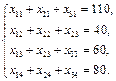
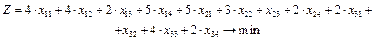

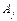
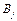
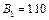
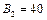
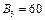
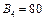

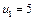
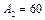
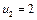
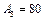
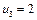

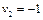
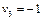
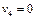
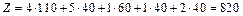 ум. од.
ум. од.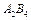 . Тепер перший план транспортної задачі є не виродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.
. Тепер перший план транспортної задачі є не виродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.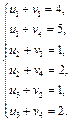
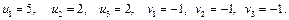 .
.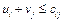 (для порожніх клітинок таблиці):
(для порожніх клітинок таблиці):
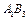 . Порушення
. Порушення  записуємо в лівому нижньому кутку відповідної клітинки.
записуємо в лівому нижньому кутку відповідної клітинки.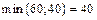 , тобто
, тобто 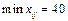 . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка
. Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка  од.,
од., 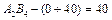 од. Клітинка
од. Клітинка 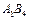 , звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (п + т- 1).
, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (п + т- 1).
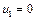
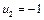

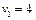

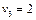
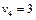
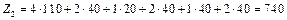 ум. од.
ум. од.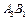 ). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю:
). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю: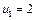
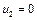
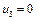
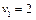
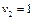
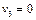
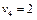
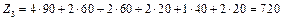 ум. од.
ум. од.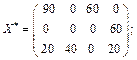
 Розглянемо приклад. Урожайність сільськогосподарських культур залежить, як відомо, від багатьох чинників, серед яких насамперед слід назвати заходи з підживлення ґрунту. Природна родючість земельних угідь забезпечує лише певний рівень продуктивності рослин. Щоб підвищити їх урожайність, використовують органічні та мінеральні добрива. Залежність урожайності цукрових буряків від кількості внесених мінеральних добрив ілюструє рис. 6.1.
Розглянемо приклад. Урожайність сільськогосподарських культур залежить, як відомо, від багатьох чинників, серед яких насамперед слід назвати заходи з підживлення ґрунту. Природна родючість земельних угідь забезпечує лише певний рівень продуктивності рослин. Щоб підвищити їх урожайність, використовують органічні та мінеральні добрива. Залежність урожайності цукрових буряків від кількості внесених мінеральних добрив ілюструє рис. 6.1.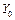 . Зі зростанням кількості внесених мінеральних добрив урожайність цієї культури підвищується. Наприклад, якщо ця кількість збільшується від
. Зі зростанням кількості внесених мінеральних добрив урожайність цієї культури підвищується. Наприклад, якщо ця кількість збільшується від 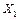 до
до 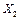 (реально це 100—280 кг діючої речовини на гектар), то врожайність цукрових буряків зростає майже лінійно, приблизно від 150 до 450 ц/га. Проте з подальшим збільшенням кількості внесених мінеральних добрив
(реально це 100—280 кг діючої речовини на гектар), то врожайність цукрових буряків зростає майже лінійно, приблизно від 150 до 450 ц/га. Проте з подальшим збільшенням кількості внесених мінеральних добрив 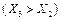 урожайність знижується
урожайність знижується 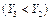 , оскільки рослини не забезпечуються іншими необхідними елементами, наприклад водою.
, оскільки рослини не забезпечуються іншими необхідними елементами, наприклад водою.
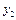
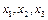 може набувати лише двох значень -1 або 0, тобто інвестиційна компанія вкладає або не вкладає кошти у відповідне підприємство.
може набувати лише двох значень -1 або 0, тобто інвестиційна компанія вкладає або не вкладає кошти у відповідне підприємство.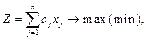
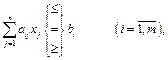


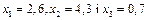 , будь-які округлення недопустимі.
, будь-які округлення недопустимі.