Приклад 15.1.Нехай булева функція від трьох змінних 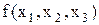 представлена таблицею істинності:
представлена таблицею істинності:
| №
| х1
| х2
| х3
| f(x1,x2,x3)
| №
| х1
| х2
| х3
| f(x1,x2,x3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За таблицею істинності можна відновити аналітичне зображення функції у вигляді ДДНФ:
 . (15.1)
. (15.1)
Отриману ДДНФ можна перетворити до вигляду:
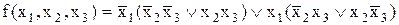 . (15.2)
. (15.2)
Схемотехнічне зображення формул (15.1) і (15.2) дає схеми з 12 і 10 контактів відповідно. Таким чином, різні форми функції описують різні схеми. Метою є зменшення кількості елементів у схемі.
Існують спеціальні методи, орієнтовані на одержання мінімальних форм функції. Серед них: Квайна, Квайна-Мак-Класки, невизначених коефіцієнтів, карт Карно, істотних змінних, граф-схем.
15.1 Основні положення методу Квайна
Нехай вихідна функція зображена у ДДНФ.
Визначення 15.1. Імпліканта функції – це деяка логічна функція, що обертається на нуль на тім же наборі змінних, на якому дорівнює нулю сама функція.
Будь-який кон’юнктивний терм або група термів, з’єднаних знаками диз’юнкції, що входять у ДДНФ, є імплікантами вихідної функції.
Визначення 15.2. Первинна імпліканта функції – це імпликанта типу елементарної кон’юнкції, ніяка частина якої вже не є імплікантою.
Завдання мінімізації за методом Квайна полягає у попарному порівнянні всіх імплікант, що входять у ДДНФ, з метою виявлення можливості поглинання якоїсь змінної на основі закону склеювання 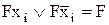 . При цьому вдається понизити ранг термів. Процедура проводиться доти, поки не залишиться жодного члена, що допускає поглинання з іншим термом. Терми, що піддалися поглинанню, відзначаються. Невідмічені терми є первинними імплікантами.
. При цьому вдається понизити ранг термів. Процедура проводиться доти, поки не залишиться жодного члена, що допускає поглинання з іншим термом. Терми, що піддалися поглинанню, відзначаються. Невідмічені терми є первинними імплікантами.
Якщо отриманий логічний вираз не виявився мінімальним, то досліджується можливість подальшого спрощення. Для цього складається таблиця, у рядках якої вказуються знайдені первинні імпліканти, а в стовпцях - терми вихідного виразу. Комірки таблиці відзначаються, якщо первинна імпліканта входить до складу якого-небудь терму. Таким чином, завдання спрощення зводиться до того, щоб знайти таку мінімальну кількість первинних імплікант, які покривають всі стовпці.
Метод Квайна включає наступні етапи:
– визначення первинних імплікант;
– розміщення міток;
– знаходження істотних імплікант;
– визначення й видалення зайвих стовпців;
– визначення й видалення зайвих первинних імплікант;
– вибір мінімального покриття;
– складання мінімальної форми вихідної функції.
15.2 Мінімізація булевих функцій за методом Квайна-Мак-Класки
Недолік методу Квайна полягає в необхідності попарного порівняння всіх термів на першому етапі при знаходженні первинних імпликант. З ростом числа вихідних термів збільшується кількість попарних порівнянь, що ускладнює розв’язок.
Метод Квайна-Мак-Класки є модифікацією методу Квайна. Він заснований на кубічному поданні термів ДНФ із попередньою розбивкою кубів на підгрупи, обумовлені однаковим числом одиниць. Розбивка дає можливість порівнювати куби тільки за сусідніми за числом одиниць групами для зменшення кількості переборів.
В ітеративній процедурі мінімізації попарне порівняння можна виконувати тільки між сусідніми групами.
Вихідне завдання функції визначається для зручності десятковими кодами двійкових кубів, що відповідають ДНФ.
Знаходження первинних імплікант на першому етапі можна спростити за допомогою числового зображення булевих функцій, а саме:
1. Всі вихідні терми записуються у вигляді їхніх двійкових номерів.
2. Всі номери розбиваються на непересічні групи за числом одиниць. Умовою утворення r-куба є наявність розбіжності в (r-1)-кубах тільки за однією координатою в одному двійковому розряді й наявність спільних незалежних координат.
3. В i-групу включають всі номери наборів, що мають у своєму записі i одиниць.
4. Попарне порівняння виконується тільки між сусідніми за номером групами. Групи, які розрізняються за двома розрядами і більше, не має сенсу порівнювати.
Приклад 15.2. Потрібно мінімізувати логічну функцію за методом Квайна-Мак-Класки:
 .
.
Розв’язок. Функція зображена числовим способом. На підставі таблиці істинності можна подати функцію в кубічній формі. Для цього слід виписати всі 0-куби, що утворюють комплекс 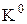 :
:
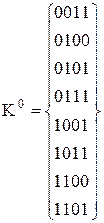 . (15.3)
. (15.3)
Слід розбити комплекс 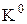 на групи за кількістю одиниць у кожному двійковому наборі. Таких груп буде три:
на групи за кількістю одиниць у кожному двійковому наборі. Таких груп буде три:
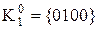 ,
,  ,
, 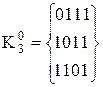 . (15.4)
. (15.4)
1) Визначення первинних імплікант.
а) Порівняння сусідніх за номером груп кубів – склеювання кубів (поглинена координата заміняється на Х):
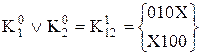 , (15.5)
, (15.5)
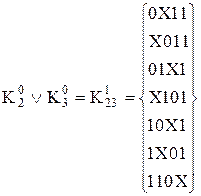 . (15.6)
. (15.6)
б) Всі 1-куби розбиваються на групи за принципом розташування незалежної координати Х (нижній індекс відповідає порядковому номеру розташування незалежної координати Х):
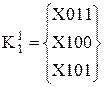 ;
; 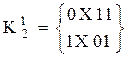 ;
; 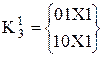 ;
; 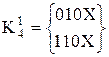 . (15.7)
. (15.7)
Куби усередині кожної групи порівнюються з метою одержання  -кубів. Порівняння кубів усередині комплексу
-кубів. Порівняння кубів усередині комплексу  дає
дає 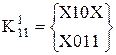 , а порівняння усередині
, а порівняння усередині 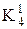 дає
дає 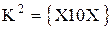 , що вже міститься в
, що вже міститься в 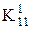 , тобто отримана первинна імпліканта другого рангу
, тобто отримана первинна імпліканта другого рангу 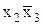 .
.
2) Складання таблиці й розміщення міток. Складається таблиця вихідних термів і тих імплікант, які не брали участь у склеюванні. Якщо у вихідний терм входить яка-небудь первинна імпліканта, то на перетинанні відповідного рядка й стовпця вказується мітка «*» (табл. 15.2).
Таблиця 15.2. Складання таблиці й розміщення міток
| Номера стовпців
|
|
|
|
|
|
|
|
|
| Набори
|
|
|
|
|
|
|
|
|
| 0X11
| *
|
|
| *
|
|
|
|
|
| X011
| *
|
|
|
|
| *
|
|
|
| 01X1
|
|
| *
| *
|
|
|
|
|
| 10X1
|
|
|
|
| *
| *
|
|
|
| 1X01
|
|
|
|
| *
|
|
| *
|
| X10X
|
| *
| *
|
|
|
| *
| *
|
3) Визначення істотних імплікант. Істотна імпліканта визначається єдиною міткою в якому-небудь стовпці таблиці. Істотною імплікантою 2-го рангу є терм 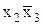 , що відповідає 2-кубу Х10Х. Стовпці, що відповідають істотній імпліканті, відокремлюються (табл. 15.3).
, що відповідає 2-кубу Х10Х. Стовпці, що відповідають істотній імпліканті, відокремлюються (табл. 15.3).
Таблиця 15.3. Визначення істотних імплікант і видалення зайвих стовпців
|
| Номера стовпців
|
|
|
|
|
|
|
|
|
|
| Набори
|
|
|
|
|
|
|
|
|
| A
| 0X11
| *
|
|
| *
|
|
|
|
|
| B
| X011
| *
|
|
|
|
| *
|
|
|
| C
| 01X1
|
|
| *
| *
|
|
|
|
|
| D
| 10X1
|
|
|
|
| *
| *
|
|
|
| E
| 1X01
|
|
|
|
| *
|
|
| *
|
|
| X10X
|
| *
| *
|
|
|
| *
| *
|
4-й і 5-й етапи, які відповідають викреслюванню зайвих стовпців і зайвих первинних імплікант, відсутні.
6) Вибір мінімального покриття. Виділяються стовпці відповідні істотним імплікантам (у цьому випадку тільки однієї істотної імпліканті). Складається таблиця для залишившихся невиділеними термів та імплікант. Вирішується завдання мінімального покриття рядків стовпцями (табл. 15.4).
Таблиця 15.4. Покриття рядків стовпцями
|
| Номери стовпців
|
|
|
|
|
|
| Набори
|
|
|
|
|
| A
| 0X11
| *
| *
|
|
|
| B
| X011
| *
|
|
| *
|
| C
| 01X1
|
| *
|
|
|
| D
| 10X1
|
|
| *
| *
|
| E
| 1X01
|
|
| *
|
|
Таким чином, обране мінімальне покриття рядків стовпцями: 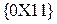 ,
,  . Воно відповідає термам
. Воно відповідає термам 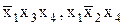 . З урахуванням отриманої раніше істотної імпліканти
. З урахуванням отриманої раніше істотної імпліканти 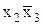 остаточне мінімальне зображення функції має вигляд:
остаточне мінімальне зображення функції має вигляд: 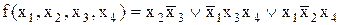 .
.
Отже, методи мінімізації булевих функцій використовуються у всіх програмних додатках, пов’язаних із синтезом обчислювальних пристроїв. Вони дозволяють у середньому на 20-30% одержати більше економічний проект із позиції апаратурних витрат. Найбільше практично орієнтованими є метод Квайна-Мак-Класки, що оперує кубічним зображенням булевих функцій. Недоліком обох методів є застосування імплікантної таблиці для розв’язання завдання знаходження мінімального покриття, що вимагає великого обсягу пам’яті для реальних об’єктів.
15.3 Контрольні питання
1. Що являє собою процес мінімізації булевих функцій?
2. За рахунок чого досягається мінімальна форма функції?
3. Які існують методи мінімізації булевих функцій?
4. Що таке імпліканта (первинна імпліканта)?
5. Які основні етапи методу Квайна?
6. Що таке істотна імпліканта?
7. Як визначаються істотні імпліканти?
8. У чому недолік методу Квайна?
9. Які основні етапи методу Квайна-Мак-Класки?
10. У чому переваги методу Квайна-Мак-Класки?
11. Як виконується вибір мінімального покриття рядків стовпцями в методах Квайна та Квайна-Мак-Класки?
16 Мінімізація булевих функцій: метод невизначених коефіцієнтів
Для мінімізації булевих функцій від невеликої кількості змінних застосовується метод невизначених коефіцієнтів у базисі І-АБО-НІ.
16.1 Основні припущення
Метод використовує наступні основні факти.
Відомо, що будь-яку булеву функцію можна зобразити в диз’юнктивній нормальній формі. Для функції від трьох змінних загальний вигляд ДНФ можна записати так:
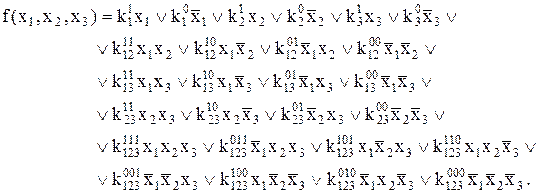 (16.1)
(16.1)
Невизначені коефіцієнти 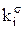 розташовані при змінних або їх кон’юнкціях, причому нижні індекси співпадають з індексами змінних, верхній – 0 або 1 залежно від того, чи мають первинні терми інверсії чи ні (0 – змінна під знаком інверсії, 1 – без інверсії). Самі невизначені коефіцієнти також приймають значення 0 або 1 і з метою мінімізації функції підбираються таким чином, щоб отримана ДНФ після цього мала мінімальну кількість букв.
розташовані при змінних або їх кон’юнкціях, причому нижні індекси співпадають з індексами змінних, верхній – 0 або 1 залежно від того, чи мають первинні терми інверсії чи ні (0 – змінна під знаком інверсії, 1 – без інверсії). Самі невизначені коефіцієнти також приймають значення 0 або 1 і з метою мінімізації функції підбираються таким чином, щоб отримана ДНФ після цього мала мінімальну кількість букв.
При визначенні ДНФ ураховують властивість: диз’юнкція деякого числа змінних дорівнює нулю, якщо всі вхідні в неї змінні дорівнюють нулю; дорівнює одиниці, якщо хоча б одна змінна дорівнює одиниці:
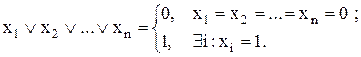 (16.2)
(16.2)
Оскільки функція від трьох змінних визначена на стандартних 8-мі двійкових наборах, праву частину формули (16.1) можна перетворити на кожному наборі змінних, у результаті чого виходить система рівнянь:
 (16.3)
(16.3)
Якщо функція приймає нульові значення на відповідному наборі змінних 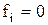 , то, згідно (16.2), всі коефіцієнти, що входять у дане рівняння, дорівнюють нулю. Тоді в інших рівняннях системи (16.3), де
, то, згідно (16.2), всі коефіцієнти, що входять у дане рівняння, дорівнюють нулю. Тоді в інших рівняннях системи (16.3), де 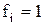 , варто також покласти рівними нулю ці коефіцієнти.
, варто також покласти рівними нулю ці коефіцієнти.
Систему (16.3) зручно зобразити у вигляді таблиці (табл. 16.1).
Нижні індекси коефіцієнтів кожного стовпця визначають номер змінних, верхні – відповідають стовпцю значень ціх змінних. В останньому стовпці таблиці вказуються значення функції на відповідному наборі змінних, які визначаються за умовою задачі. Передбачається також, що всі коефіцієнти в довільному рядку пов’язані символами диз'юнкції.
Таблиця 16.1. Подання системи рівнянь (16.3) за допомогою таблиці
16.2 Алгоритм знаходження невизначених коефіцієнтів
Алгоритм включає наступні етапи:
1) Цикл за рядками – перегляд нульових рядків: вибрати рядок системи (16.3), у якій функція приймає нульове значення 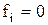 . Дорівняти нулю всі коефіцієнти цього рядка.
. Дорівняти нулю всі коефіцієнти цього рядка.
2) Якщо всі нульові рядки переглянуті, то перейти до пункту 3, інакше - повернутися до пункту 1.
3) Викреслювання рівних нулю коефіцієнтів з рядків з одиницями: із всіх рядків, де 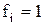 , викреслити рівні нулю коефіцієнти, визначені в пункті 1.
, викреслити рівні нулю коефіцієнти, визначені в пункті 1.
4) Модифікована система рівнянь: переписати систему (16.3) з урахуванням виконаних перетворень.
5) Вибір мінімального покриття: у модифікованій системі вибрати й покласти рівними одиниці мінімальну кількість коефіцієнтів з мінімальним числом індексів, щоб задовольнити дану систему.
6) Визначення мінімальної форми функції: скласти мінімальну ДНФ за обраними коефіцієнтами.
Приклад 16.1. Мінімізувати функцію від трьох змінних Y=1 на наборах {1, 2, 3, 4} методом невизначених коефіцієнтів з одержанням МДНФ.
Розв’язок. Таблицю невизначених коефіцієнтів можна зобразити в спрощеному вигляді (табл. 16.2).
Таблиця 16.2. Спрощений вигляд таблиці функції 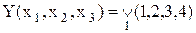 для методу невизначених коефіцієнтів
для методу невизначених коефіцієнтів
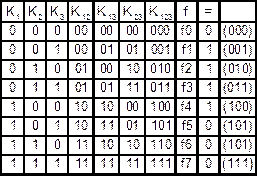
Тут у заголовок таблиці винесені з відповідних стовпців невизначені коефіцієнти із спільними нижніми індексами, верхні індекси при цьому зберігаються у відповідних комірках кожного стовпця.
Коефіцієнти рядків, де 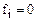 , дорівнюються нулю. З рядків, де
, дорівнюються нулю. З рядків, де 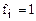 , викреслюються коефіцієнти, що зустрічаються в рядках, де
, викреслюються коефіцієнти, що зустрічаються в рядках, де 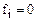 .
.
Виписуються коефіцієнти, що залишилися, з одержанням тим самим модифікованої системи:
 (16.4)
(16.4)
З (16.4) мінімальний результат відповідає формі:
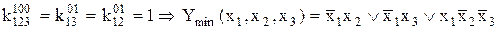 .
.
16.3 Контрольні питання
1. На яких основних положеннях базується метод невизначених коефіцієнтів?
2. Яке узагальнене подання ДНФ функції від трьох змінних?
3. Які основні етапи алгоритму знаходження невизначених коефіцієнтів?
4. У якому базисі повинна бути представлена функція, щоб для мінімізації можна було застосувати метод невизначених коефіцієнтів?
5. Коли диз’юнкція деякої кількості коефіцієнтів дорівнює нулю?
6. Коли диз’юнкція деякої кількості коефіцієнтів дорівнює одиниці?
7. Як вибирається розв’язок модифікованої системи рівнянь у методі невизначених коефіцієнтів?
8. Скільки рядків має вихідна система рівнянь при мінімізації функції від чотирьох змінних методом невизначених коефіцієнтів?
9. Що являє собою мінімальне покриття в методі невизначених коефіцієнтів?
17 Мінімізація булевих функцій: метод карт Карно
Для мінімізації булевих функцій використовується метод мінімізуючих карт, які називаються картами Карно. Заснований на графічному зображенні булевих функцій від невеликого числа змінних, де коди змінних у сусідніх координатах завдання функції є сусідніми.
17.1 Основні положення
Таблиці істинності функції від двох, трьох і чотирьох змінних можуть бути перебудовані в карти Карно (рис. 17.1-17.3).
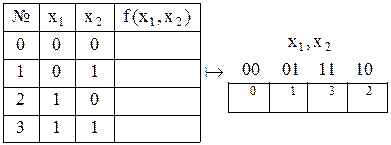
Рис. 17.1. Карта Карно для функції від двох змінних
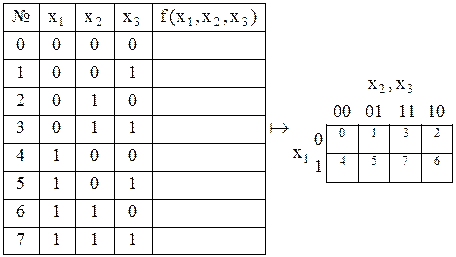
Рис. 17.2. Карта Карно для функції від трьох змінних
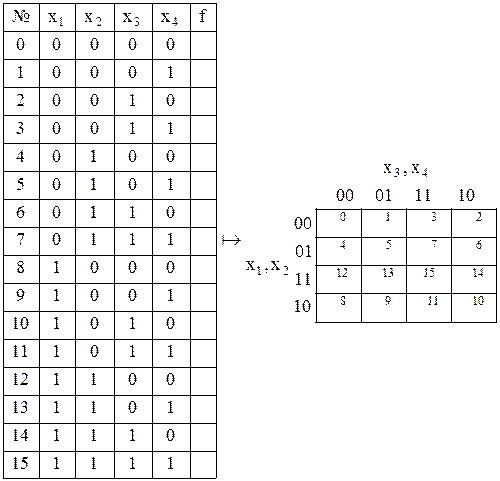
Рис. 17.3. Карта Карно для функції від чотирьох змінних
Карти Карно мають наступні властивості:
1) Карти організовані таким чином, що сусідні за рядками або за стовпцями клітки відрізняються значенням тільки однієї змінної.
2) Якщо дві комбінації значень змінних відрізняються тільки за однією координатою, то клітки є сусідніми.
3) У карті Карно дві змінні клітки на протилежних кінцях карти теж є сусідніми. Ця властивість зберігається для карт Карно трьох і чотирьох змінних: протилежні кінці кожного рядка або стовпця є сусідніми.
Для зображення функції на карті досить у ті клітки, де функція дорівнює одиниці, помістити одиниці. Вважається, що в інших клітках розташовані нулі.
Приклад 17.1. Зобразити функцію 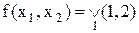 на карті Карно.
на карті Карно.
Розв’язок. Функція від двох змінних зображена числовим способом. Щоб представити дану функцію на Карті, треба в 1-у та 2-у комірки карти Карно для двох змінних помістити одиничні значення функції, як показано нижче:
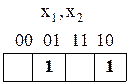
Зауваження: тут і далі номера осередків, які відповідають двійковим наборам, опускаються для спрощення запису.
За картою, як і за таблицею істинності, можна відновити аналітичну форму функції у вигляді ДДНФ:
 .
.
17.2 Спрощений стандарт карт Карно
Поряд зі звичайним уводиться в розгляд спрощений стандарт карт Карно. Замість перерахування двійкових наборів поєднуються за допомогою фігурних стрілок групи, яким відповідають одиничні значення змінних (рис. 17.4).


а б в
Рис. 17.4. Спрощений стандарт карти Карно для функції: а – від двох змінних; б – від трьох змінних; в – від чотирьох змінних
Приклад 17.2. Представити функцію 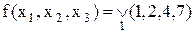 на карті й одержати СДНФ.
на карті й одержати СДНФ.
Розв’язок. Якщо скористатися спрощеним стандартом карт Карно, зображення функції буде виглядати так:
 ,
,
а відповідна ДДНФ при цьому:
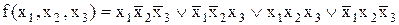 .
.
Таким чином, для спрощення позначень рядки й стовпці, що містять змінну 1, позначають фігурною дужкою. При цьому значення 0 ця змінна має у невідмічених комірках.
17.3 Мінімізація за картами Карно
Комірки з одиницями на карті називаються Р-клітинами.
Дві сусідні одиниці утворюють одномірний р-підкуб або 1-куб. Одновимірний р-підкуб відповідає добутку, у якому завжди відсутній один первинний терм.
Змінна, відсутня у добутку, визначається за картою – вона має різні значення для двох одиниць відповідного підкуба.
Приклад 17.3. Зобразити функцію 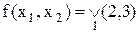 на карті Карно.
на карті Карно.
Розв’язок. Відзначимо одиничні значення функції на карті, помістивши їх у другу й третю комірки (рис. 17.5).
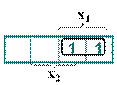
Рис. 17.5. Одновимірний р-подкуб або 1-куб
При цьому видно, що дві одиниці попадають у сусідні комірки й утворюють 1-куб. Вони обводяться мінімізуючим контуром. Отже, зображення функції буде таким: 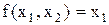 .
.
Чотири сусідні одиниці утворюють двовимірний р-підкуб (2-куб), що відповідає добутку без двох первинних термів. Ті змінні, які не зберігають постійне значення на цьому підкубі, не вказуються.
Приклад 17.4. Знайти аналітичний вираз, що відповідає 2-кубу на карті Карно (рис. 17.6).
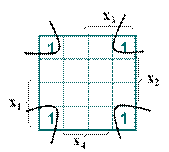
Рис. 17.6. Двовимірний р-підкуб або 2-куб на карті Карно 4-х змінних
Розв’язок. Одиниці попадають у кутові комірки карти, які є сусідніми. Спільними для всіх чотирьох комірок є 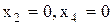 , чому відповідає кон’юнктивний терм
, чому відповідає кон’юнктивний терм  , що описує 2-куб. Отже, мінімальна форма функції, отримана за картою:
, що описує 2-куб. Отже, мінімальна форма функції, отримана за картою: 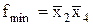 .
.
Тривимірні р-підкуби містять по 8 одиниць (3-куб).
Приклад 17.5. Блок з 8-мі одиниць підлягає склеюванню з одержанням 3-кубу (рис. 17.7).

Рис. 17.7. Тривимірний р-підкуб або 3-куб
При цьому мінімальна форма функції описується виразом, якому відповідає єдиний превинний терм: 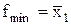 .
.
Одновимірний р-підкуб відповідає ребру, що має дві сусідні вершини. Двовимірний р-підкуб відповідає двовимірному підкубу n-вимірного куба.
Правила мінімізації:
1) Дві сусідні комірки на карті утворюють 1-куб.
2) Несуттєва координата для двох кубів позначається символом X. Наприклад: 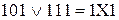 .
.
3) Чотири комірки поєднуються та утворюють 2-куб:
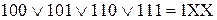 .
.
4) У загальному випадку можуть поєднуватися сусідні комірки, число яких дорівнює 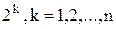 , тобто 2,4,8,16,32,..., з утворенням k-кубів, де
, тобто 2,4,8,16,32,..., з утворенням k-кубів, де 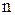 – кількість змінних функції.
– кількість змінних функції.
Стратегія одержання мінімальної ДНФ за картою Карно: треба мінімальною кількістю кубів покрити (склеїти) всі одиничні комірки карти, де кожна склейка повинна містити максимально можливе число одиниць.
17.4 Контрольні питання
1. Як складаються карти Карно для функцій від двох, трьох і чотирьох змінних?
2. Чим відрізняються карти Карно від таблиць істинності?
3. Яке основне призначення карт Карно?
4. Як установлюється зв'язок між двійковими наборами й комірками карти Карно двох (трьох, чотирьох) змінних?
5. Які комірки карти є сусідніми?
6. Як представляється функція на карті?
7. У чому полягає спрощений стандарт карт Карно?
8. Які властивості мають карти Карно?
9. Що таке р-клітки?
10. Які основні правила склеювання за картами?
11. Як виконується мінімізація за картами Карно?
12. Що являють собою мінімізуючі контури?


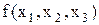 представлена таблицею істинності:
представлена таблицею істинності: . (15.1)
. (15.1)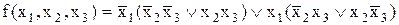 . (15.2)
. (15.2)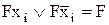 . При цьому вдається понизити ранг термів. Процедура проводиться доти, поки не залишиться жодного члена, що допускає поглинання з іншим термом. Терми, що піддалися поглинанню, відзначаються. Невідмічені терми є первинними імплікантами.
. При цьому вдається понизити ранг термів. Процедура проводиться доти, поки не залишиться жодного члена, що допускає поглинання з іншим термом. Терми, що піддалися поглинанню, відзначаються. Невідмічені терми є первинними імплікантами. .
.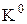 :
: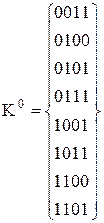 . (15.3)
. (15.3)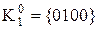 ,
,  ,
, 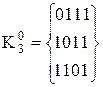 . (15.4)
. (15.4)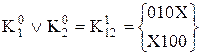 , (15.5)
, (15.5)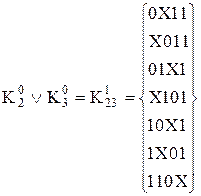 . (15.6)
. (15.6)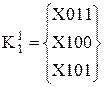 ;
; 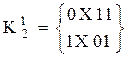 ;
; 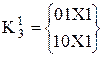 ;
; 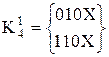 . (15.7)
. (15.7)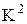 -кубів. Порівняння кубів усередині комплексу
-кубів. Порівняння кубів усередині комплексу 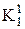 дає
дає 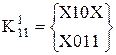 , а порівняння усередині
, а порівняння усередині 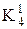 дає
дає 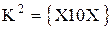 , що вже міститься в
, що вже міститься в 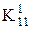 , тобто отримана первинна імпліканта другого рангу
, тобто отримана первинна імпліканта другого рангу 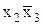 .
.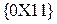 ,
,  . Воно відповідає термам
. Воно відповідає термам 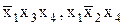 . З урахуванням отриманої раніше істотної імпліканти
. З урахуванням отриманої раніше істотної імпліканти 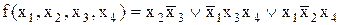 .
.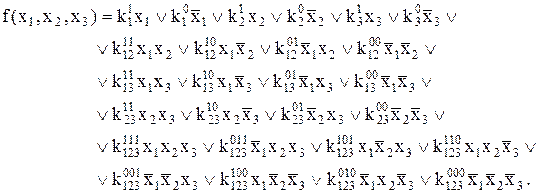 (16.1)
(16.1)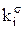 розташовані при змінних або їх кон’юнкціях, причому нижні індекси співпадають з індексами змінних, верхній – 0 або 1 залежно від того, чи мають первинні терми інверсії чи ні (0 – змінна під знаком інверсії, 1 – без інверсії). Самі невизначені коефіцієнти також приймають значення 0 або 1 і з метою мінімізації функції підбираються таким чином, щоб отримана ДНФ після цього мала мінімальну кількість букв.
розташовані при змінних або їх кон’юнкціях, причому нижні індекси співпадають з індексами змінних, верхній – 0 або 1 залежно від того, чи мають первинні терми інверсії чи ні (0 – змінна під знаком інверсії, 1 – без інверсії). Самі невизначені коефіцієнти також приймають значення 0 або 1 і з метою мінімізації функції підбираються таким чином, щоб отримана ДНФ після цього мала мінімальну кількість букв.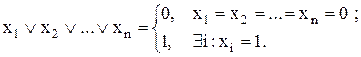 (16.2)
(16.2) (16.3)
(16.3)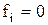 , то, згідно (16.2), всі коефіцієнти, що входять у дане рівняння, дорівнюють нулю. Тоді в інших рівняннях системи (16.3), де
, то, згідно (16.2), всі коефіцієнти, що входять у дане рівняння, дорівнюють нулю. Тоді в інших рівняннях системи (16.3), де 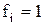 , варто також покласти рівними нулю ці коефіцієнти.
, варто також покласти рівними нулю ці коефіцієнти.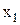

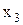
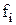

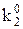
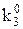
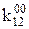
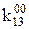

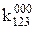
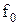
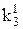
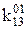
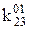

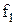
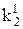
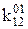
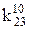
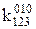
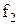
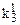
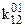
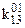
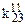
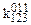



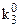
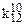
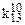
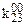

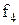

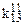
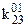
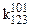
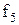
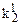
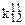
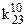

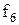
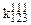
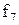
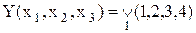 для методу невизначених коефіцієнтів
для методу невизначених коефіцієнтів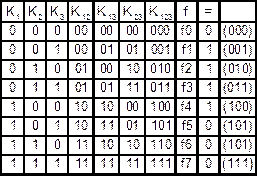
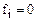 , дорівнюються нулю. З рядків, де
, дорівнюються нулю. З рядків, де 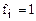 , викреслюються коефіцієнти, що зустрічаються в рядках, де
, викреслюються коефіцієнти, що зустрічаються в рядках, де  (16.4)
(16.4)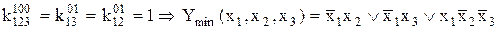 .
.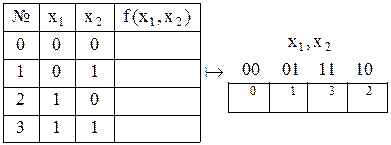
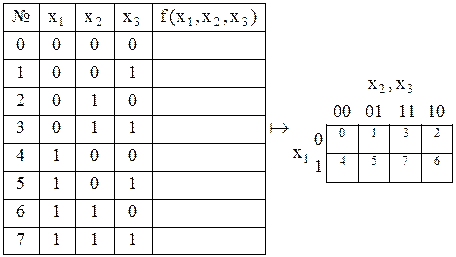
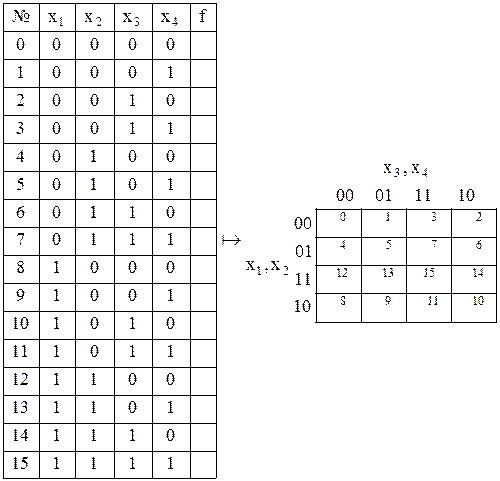
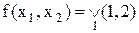 на карті Карно.
на карті Карно.
 .
.

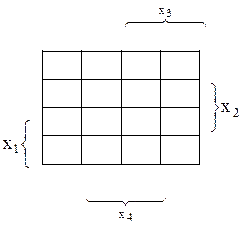
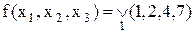 на карті й одержати СДНФ.
на карті й одержати СДНФ. ,
,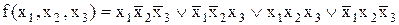 .
.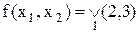 на карті Карно.
на карті Карно.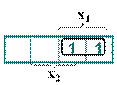
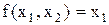 .
.
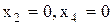 , чому відповідає кон’юнктивний терм
, чому відповідає кон’юнктивний терм  , що описує 2-куб. Отже, мінімальна форма функції, отримана за картою:
, що описує 2-куб. Отже, мінімальна форма функції, отримана за картою: 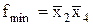 .
.
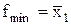 .
.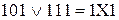 .
.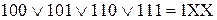 .
. , тобто 2,4,8,16,32,..., з утворенням k-кубів, де
, тобто 2,4,8,16,32,..., з утворенням k-кубів, де 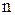 – кількість змінних функції.
– кількість змінних функції.