Результати з першого й другого блоків використовуються як вхідні канали (лінії 6 і 7 відповідно) для блоку-диз’юнктора 3, де вони складаються, і результатом при цьому є вихід 8: 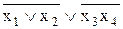 .
.
Блок 4 являє собою кон’юнктор, на який як вхідні змінні подаються значення каналів 8 і 5, де останнім каналом є змінна 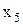 . Таким чином, результат –вихід 9 – описується наступним логічним виразом:
. Таким чином, результат –вихід 9 – описується наступним логічним виразом:
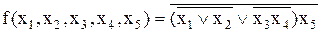 .
.
11.5 Контрольні питання й завдання
1. Як визначається фізичний зміст функцій кон’юнкція, диз’юнкція, інверсія в термінах логічних операторів?
2. Перелічити основні логічні примітиви, які використовуються при синтезі логічних схем.
3. Які IEEE-стандарти логічних блоків використовуються для опису логічних схем?
4. Які основні властивості суми за модулем два?
5. Як визначається функція Шефера?
6. Як визначається функція Веба?
12 Способи зображення булевих функцій
Розглядаються основні способи зображення булевих функцій (БФ) для опису цифрових проектів: табличний, числовий, аналітичний, геометричний, кубічний, схемотехнічний. Визначається зв’язок між ними.
12.1 Табличний спосіб зображення булевих функцій
Булева функція може задаватися за допомогою таблиці істинності. У цьому випадку напроти двійкових наборів, де функція приймає значення 1, вказуються 1, напроти інших наборів – нульові значення функції.
Приклад 12.1. Нехай функція від трьох змінних представлена таблицею істинності:
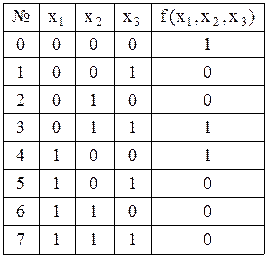
З таблиці видно, що дана функція приймає значення 1 на 0-м, 3-м і 4-м двійкових наборах, на інших наборах значення функції дорівнюють нулю. При цьому не зазначено, яким аналітичним виразом задана функція.
12.2 Числовий спосіб зображення булевих функцій
Числовий спосіб використовується для спрощення зображення функцій алгебри логіки. Він ґрунтується на зв’язку двійкової й десяткової систем числення. Оскільки номера двійкових наборів є їхні десяткові еквіваленти, у числовому способі можна перераховувати тільки ті набори, де функція приймає одиничні значення, тобто замість повного перерахування термів вказуються десяткові еквіваленти (порядкові номери) двійкових наборів, на яких функція приймає значення 1, що дійсно спрощує форму запису.
Приклад 12.2.Функції з таблиці істинності в прикладі 12.1 відповідає числове подання 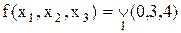 або
або 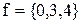 . В останньому записі передбачається залежність функції від трьох змінних.
. В останньому записі передбачається залежність функції від трьох змінних.
12.3 Аналітична форма запису булевих функцій
За таблицею істинності можна одержати аналітичну форму запису, наприклад, ДДНФ або ДКНФ, а потім при необхідності спростити їх до ДНФ і КНФ.
Приклад 12.3. Відновити аналітичну форму функції за таблицею істинності із приклада 12.1.
Розв’язок. ДДНФ виписується за одиничним значенням функції, які досягаються на наборах 0, 3 і 4:
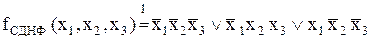 ,
,
а ДКНФ – за нульовим значенням, яким відповідають всі інші двійкові набори:

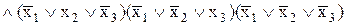 .
.
Отриману ДДНФ можна спростити шляхом склеювання крайніх кон’юнктивних термів, які відрізняються тільки за першою координатою. Отримана в результаті скорочена ДНФ буде такою:
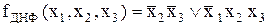 .
.
ДКНФ також підлягає скороченню шляхом склеювання кон’юнктивних термів, що відрізняються тільки за однією координатою:
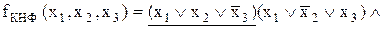
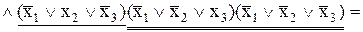
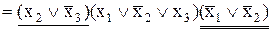 .
.
Таким чином, будь-яка булева функція може бути відновлена з таблиці істинності й зображена у вигляді ДДНФ, ДКНФ, а також ДНФ, КНФ. ДНФ і КНФ є скорочені форми запису ДДНФ і ДКНФ.
12.4 Геометрична інтерпретація булевих функцій
Геометричний спосіб подання булевых функцій використовується для інтерпретації перетворень над логічними виразами.
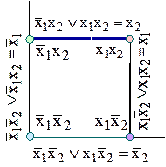
Наприклад, булеву функцію від двох змінних зображують на площині наступним чином. На рис. 12.1, б, вершини одиничного квадрата позначені довільними змінними. які утворюють кон’юнктивні терми на кожному двійковому наборі. Сусідні терми, що відрізняються тільки за однією координатою, склеюються уздовж з’єднуючого їх ребра, у результаті чого ребра позначаються спільною для вершин координатою.
а б
Рис. 12.1. Геометрична інтерпретація довільної булевої функції від двох змінних: а – розташування двійкових наборів; б – позначення вершин і ребер
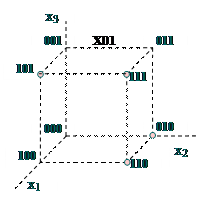
Для функції трьох змінних геометричне зображення виконують у вигляді куба, де вершини також позначаються десятковими цифрами, двійковими цифрами, довільними змінними. При цьому ребра куба поглинають вершини, а грані поглинають ребра (рис. 12.2).
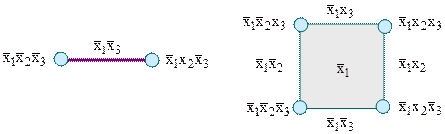
Рис. 12.2. Склеювання вершин і ребер одиничного куба при геометричному зображенні булевої функції від трьох змінних
При геометричному зображенні булевої функції точками позначаються вершини, у яких дана функція приймає одиничні значення.
Приклад 12.4.Побудувати графік булевої функції 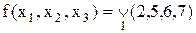 .
.
Розв’язок. Щоб представити дану функцію геометрично, слід відмітити вершини куба з номерами 2,5,6 і 7, на яких досягаються одиничні значення функції (рис. 12.3).
Рис. 12.3. Геометрична інтерпретація функції 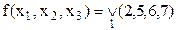
У геометричному змісті кожний двійковий набір може розглядатися як n-мірний двійковий вектор, що визначає точку n-мірного простору. Множина наборів, на яких визначена функція, представляється у вигляді вершин n-мірного куба.
12.5 Кубічна форма зображення булевих функцій
Якщо вершини позначені у двійковому коді, як показано на рис. 12.4, то при склеюванні сусідніх пар вершин ребро позначається набором з незалежною координатою Х, за якою відрізняються двійкові набори. При цьому говорять, що Х змінюється уздовж даного ребра.

Рис. 12.4. Склеювання вершин і ребер одиничного куба при геометричному зображенні булевої функції від трьох змінних у термінах двійкових наборів
Терм максимального рангу називається 0-кубом і геометрично інтерпретується як точка – вершина одиничного кубу.
Склеювання 0-кубів дає відрізок (1-куб), склеювання відрізків є грань (2-куб), склеювання граней - куб.
Геометрично кубами можна відзначати елементи (вершини, ребра, грані) одиничного куба (рис. 12.5).
Кубічне зображення використовується при мінімізації булевих функцій, зокрема, у методі Квайна-Мак-Класки.
Рис. 12.5. Кубічне позначення вершин і ребер
Приклад 12.5.Одержати скорочену ДНФ за числовою формою функції  .
.
Розв’язок. За вказаними двійковими наборами, на яких функція приймає значення 1, слід скласти комплекс 0-кубів:
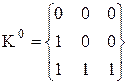 .
.
0-куби усередині цього комплексу, що відрізняються за однією координатою склеюються з одержанням 1-куба або відрізка. Тим самим виділяється підкомплекс з 1-кубу:  , якому відповідає терм
, якому відповідає терм  . Він у сукупності із 0-кубом (1,1,1), що залишився та якому відповідає терм
. Він у сукупності із 0-кубом (1,1,1), що залишився та якому відповідає терм  , аналітична форма визначається у вигляді скороченої ДНФ:
, аналітична форма визначається у вигляді скороченої ДНФ:
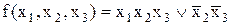 .
.
12.6 Схемотехнічне зображення
Як було показано в підрозділі 11, якщо функція задана аналітично (логічним виразом), то йому можна зіставити логічну схему. І навпаки: якщо є схема, то її можна описати аналітично, тобто зіставити їй логічний вираз. Для схемотехнічного зображення булевих функцій існують примітиви – елементарні логічні блоки, з яких синтезують схему.
Таким чином, одну булеву функцію можна зобразити різними способами залежно від потреб розв’язуваних завдань.
12.7 Контрольні питання й завдання
1. Встановити зв’язок між табличним і числовим способами зображення булевих функцій.
2. Проаналізувати зв’язок між табличною, аналітичною й кубічною формами зображення булевих функцій.
3. Як можна описати зв’язок між геометричною й кубічною інтепретацією булевих функцій?
4. Як геометрично інтерпретується 0-куб?
5. Коли можна виконувати склеювання 0-кубів?
6. Як геометрично інтерпретується склеювання 0-кубів?
7. Що є результатом склеювання 0-кубів?
8. Що являє собою 1-куб?
9. Як інтерпретується 2-куб?
10. Що являє собою грань одиничного куба?
11. Як геометрично можна зобразити булеву функцію від двох змінних?
12. Як геометрично можна інтерпретувати булеву функцію від трьох змінних?
13. Яка кубічна інтерпретація булевої функції?
14. Як з комплексу 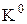 одержати підкомплекс
одержати підкомплекс  ?
?
15. Як відновити функцію в якій-небудь формі із числового способу зображення?
16. Як відновити функцію з таблиці істинності?
17. Який зв’язок схемотехнічної і аналітичної форм зображення булевих функцій?
13 Системи функцій алгебри логіки. Функціональна повнота
Розглядаються основні властивості функціонально повних систем для опису й синтезу цифрових проектів
13.1 Класи булевих функцій
Уводяться в розгляд п’ять класів булевих функцій:
1) клас функцій, що зберігають константу нуль ( 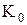 );
);
2) клас функцій, що зберігають константу одиниця ( 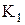 );
);
3) клас самодвоїстих функцій 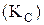 ;
;
4) клас монотонних функцій (  );
);
5) клас лінійних функцій 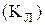 .
.
Клас функцій, що зберігають нуль (К0), містить всі функції, які приймають нульове значення при всіх нульових значеннях змінних.
Визначення 13.1.Якщо булева функція на нульовому наборі змінної дорівнює нулю, то функція зберігає константу нуль:
 . (13.1)
. (13.1)
Клас функцій, що зберігають одиницю (К1), включає всі функції, які на наборі з одиниць приймають значення одиниця.
Визначення 13.2.Якщо булева функція на одиничному наборі (наборі з одиниць) дорівнює одиниці, то говорять, що функція зберігає одиницю:
 . (13.2)
. (13.2)
Перш ніж розглядати клас лінійних функцій (КЛ), необхідно ввести наступні допоміжні поняття.
Визначення 13.3. Формули, що містять знаки  , називаються поліномами.
, називаються поліномами.
Визначення 13.4.Вираз вигляду 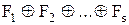 , де
, де 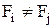 та
та 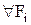 ,
, 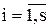 є або 1, або змінна, або кон’юнкція різних змінних, називається поліномом Жегалкіна.
є або 1, або змінна, або кон’юнкція різних змінних, називається поліномом Жегалкіна.
Теорема Жегалкіна.Будь-яка булева функція може бути зображена поліномом вигляду
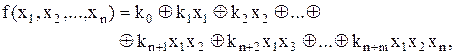 (13.3)
(13.3)
де 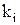 – коефіцієнти, що приймають значення 0 або 1:
– коефіцієнти, що приймають значення 0 або 1: 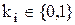 ; тобто будь-який поліном може бути перетворений у поліном Жегалкіна.
; тобто будь-який поліном може бути перетворений у поліном Жегалкіна.
Визначення 13.5.Булева функція називається лінійною, якщо вона може бути зображена поліномом першого ступеня, тобто виразом вигляду
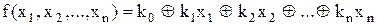 ,
, 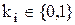 . (13.4)
. (13.4)
Кількість лінійних функцій дорівнює 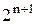 , де
, де 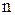 − число змінних, від яких залежить булева функція.
− число змінних, від яких залежить булева функція.
Приклад 13.1. Одержати всі лінійні функції від двох змінних.
Розв’язок. Кількість лінійних функцій від двох змінних визначається як 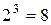 . Лінійна булева функція від двох змінних може бути зображена у вигляді полінома першого ступеня й, відповідно до формули (13.4), виражається таким способом:
. Лінійна булева функція від двох змінних може бути зображена у вигляді полінома першого ступеня й, відповідно до формули (13.4), виражається таким способом:
 ,
, 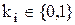 . (13.5)
. (13.5)
Коефіцієнти 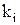 приймають значення з множини
приймають значення з множини 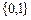 й утворюють двійкові набори, при підстановці яких у вираз (13.5) випливає вся сукупність лінійних функцій (табл. 13.1):
й утворюють двійкові набори, при підстановці яких у вираз (13.5) випливає вся сукупність лінійних функцій (табл. 13.1):
Таблиця 13.1. Клас лінійних функцій від двох змінних
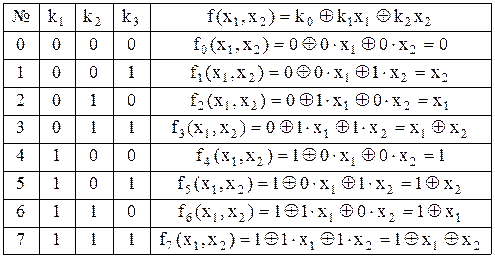
Якщо довільну булеву функцію від двох змінних шляхом еквівалентних перетворень можна зобразити в одній із вказаних восьми форм, то така функція є лінійною, тобто належить класу 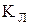 .
.
До класу монотонних функцій (КМ) відносяться такі, для яких виконана умова монотонності: на кожній парі порівнянних двійкових наборів значення функції повинні бути порівнянні в тому ж порядку.
Множина {0,1} упорядковується за принципом порівнянності: 0<1 (0 порівняний з одиницею). Нехай 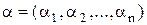 ,
, 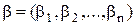 – двійкові набори,
– двійкові набори, 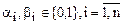 .
.
Визначення 13.6. Набір  передує набору
передує набору 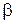 (
(  або
або  ), якщо виконується покоординатна порівнянність:
), якщо виконується покоординатна порівнянність: 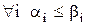 , причому хоча б для одного значення
, причому хоча б для одного значення  має місце строга нерівність
має місце строга нерівність 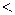 .
.
Визначення 13.7.Функція називається монотонною, якщо для будь-яких наборів  і
і 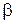 таких, що
таких, що  , виконується нерівність:
, виконується нерівність:
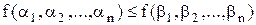 , (13.6)
, (13.6)
тобто на кожній парі порівнянних двійкових наборів значення функції повинні бути порівнянні.
Приклад 13.2. Обґрунтувати, чи належить функція 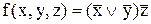 до класу монотонних.
до класу монотонних.
Розв’язок.Слід скласти таблицю істинності булевої функції 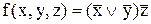 (табл. 13.2).
(табл. 13.2).
Таблиця 13.2. Значення функції 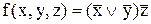
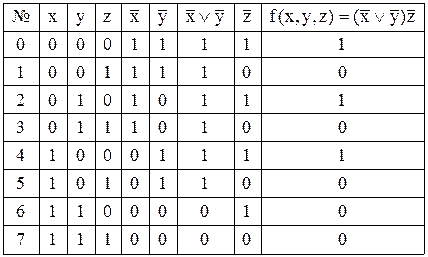
Для дослідження функції на монотонність зображується гіперкуб (рис. 13.1), у якому всі двійкові набори впорядковані за принципом порівнянності. Така структура є стандартною для будь-якої функції від трьох змінних.
Рис. 13.1. Гіперкуб для функції від трьох змінних
У вершини гіперкуба додаються значення функції на відповідних двійкових наборах (рис.13.2).
Рис. 13.2. Розподіл значень функції 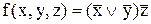 в гіперкубі
в гіперкубі
Аналіз розподілу значень функції в гіперкубі показує, що функція не є монотонною, оскільки існують нулі, що покривають одиниці, а саме: 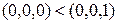 , але
, але  .
.
Таким чином, функція не належить до класу монотонних:  .
.
Для класу самодвоїстих функцій (КС) слід розглянути поняття двоїстої функції.
Визначення 13.8.Булева функція 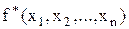 називається двоїстою для функції
називається двоїстою для функції 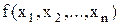 , якщо таблицю істинності для
, якщо таблицю істинності для 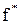 можна одержати з таблиці для
можна одержати з таблиці для 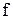 , замінивши в значеннях аргументу й функції 0 на 1 і 1 на 0, тобто має місце рівність
, замінивши в значеннях аргументу й функції 0 на 1 і 1 на 0, тобто має місце рівність
 . (13.7)
. (13.7)
Приклад 13.3. Кон’юнкція й диз’юнкція двоїсті один одному, інверсія двоїста сама собі:
1)  ,
, 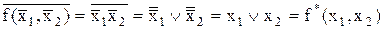 ;
;
2) Інвертуємо таблицю істинності кон’юнкції, замінивши на протилежні значення аргументів і самої функції (табл. 13.3).
Таблиця 13.3. Подвійність кон’юнкції та диз’юнкції за таблицями істинності
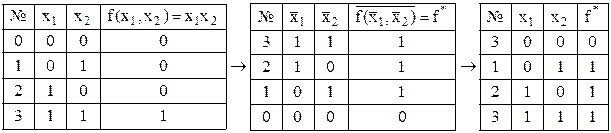
Визначення 3.14.Функція, що співпадає зі своєю двоїстою, називається самодвоїстою:
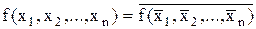 . (13.8)
. (13.8)
Самодвоїста функція на протилежних двійкових наборах 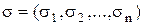 і
і  ,
, 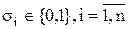 приймає протилежні значення.
приймає протилежні значення.
Приклад 13.4. Показати, що функція 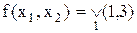 самодвоїста.
самодвоїста.
Розв’язок. Слід перетворити таблицю істинності функції (табл. 13.4).
Таблиця 13.4. Самодвоїстість функції 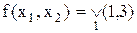

Видно, що в результаті перетворень функція не змінилася, отже, вона самодвоїста.
Принцип двоїстості.Якщо у формулі алгебри логіки 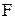 замінити знаки всіх логічних функцій на знаки двоїстих функцій, то вийде двоїста формула
замінити знаки всіх логічних функцій на знаки двоїстих функцій, то вийде двоїста формула 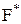 , що реалізує функцію, двоїсту тієї, яка реалізується формулою
, що реалізує функцію, двоїсту тієї, яка реалізується формулою 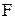 . При цьому якщо формули рівні
. При цьому якщо формули рівні 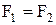 , то вірна рівність двоїстих формул
, то вірна рівність двоїстих формул 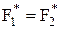 , що називається двоїстою попередній.
, що називається двоїстою попередній.
Приклад 13.5. Можна показати, що наступні рівності двоїсті один одному:
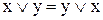 ,
, 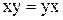 , (13.9)
, (13.9)
 ,
, 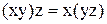 , (13.10)
, (13.10)
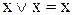 ,
, 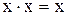 , (13.11)
, (13.11)
 ,
, 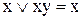 . (13.12)
. (13.12)
КНФ і ДНФ двоїсті один одному.
Властивості булевих функцій від двох змінних щодо приналежності їх до класів представлені в таблиці 13.5.
Таблиця 13.5. Приналежність булевих функцій від двох змінних класам
| Функція
| 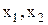
| Класи
|
|
|
|
|
| 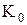
| 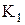
| 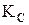
| 
| 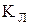
|
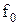
|
|
|
|
| +
|
|
| +
| +
|
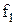
|
|
|
|
| +
| +
|
| +
|
|
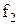
|
|
|
|
| +
|
|
|
|
|
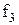
|
|
|
|
| +
| +
| +
| +
| +
|
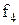
|
|
|
|
| +
|
|
|
|
|
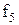
|
|
|
|
| +
| +
|
|
| +
|
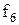
|
|
|
|
| +
|
|
|
| +
|
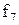
|
|
|
|
| +
| +
|
| +
|
|
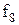
|
|
|
|
| −
| −
| −
| −
| −
|
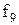
|
|
|
|
|
| +
|
|
| +
|
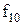
|
|
|
|
|
|
|
|
| +
|
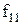
|
|
|
|
|
| +
|
|
|
|
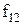
|
|
|
|
|
|
| +
|
| +
|
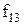
|
|
|
|
|
| +
|
|
|
|
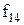
|
|
|
|
| −
| −
| −
| −
| −
|
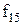
|
|
|
|
|
| +
|
| +
|
|
13.2 Повнота функцій алгебри логіки
Визначення 13.15.Система функцій алгебри логіки  називається функціонально повною, якщо кожна ФАЛ
називається функціонально повною, якщо кожна ФАЛ 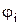 з
з  може бути реалізована формулою, що містить тільки символи функцій із цієї системи.
може бути реалізована формулою, що містить тільки символи функцій із цієї системи.
Приклад 13.6.Функціонально повними є системи:
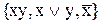 ,
, 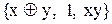 ,
, 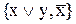 .
.
Теорема Поста-Яблонського (критерій функціональної повноти). Для того щоб ФАЛ 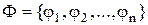 була повної необхідно й досить, щоб вона містила хоча б одну функцію, яка
була повної необхідно й досить, щоб вона містила хоча б одну функцію, яка
1) не зберігає нуль – 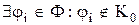 ;
;


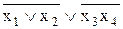 .
.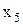 . Таким чином, результат –вихід 9 – описується наступним логічним виразом:
. Таким чином, результат –вихід 9 – описується наступним логічним виразом: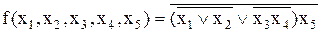 .
.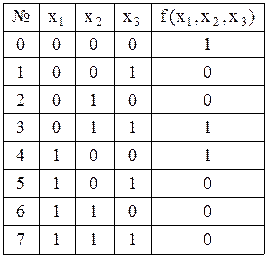
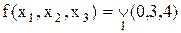 або
або 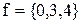 . В останньому записі передбачається залежність функції від трьох змінних.
. В останньому записі передбачається залежність функції від трьох змінних.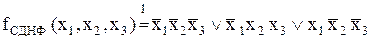 ,
,
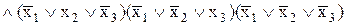 .
.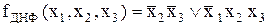 .
.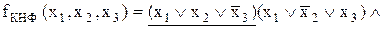
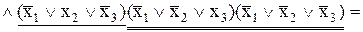
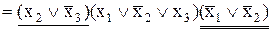 .
.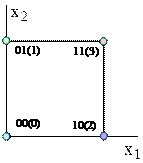
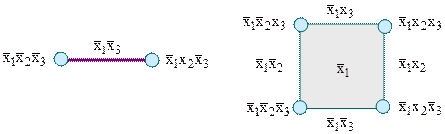
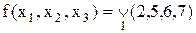 .
.
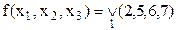


 .
.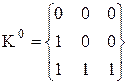 .
. , якому відповідає терм
, якому відповідає терм  . Він у сукупності із 0-кубом (1,1,1), що залишився та якому відповідає терм
. Він у сукупності із 0-кубом (1,1,1), що залишився та якому відповідає терм  , аналітична форма визначається у вигляді скороченої ДНФ:
, аналітична форма визначається у вигляді скороченої ДНФ: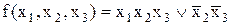 .
.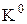 одержати підкомплекс
одержати підкомплекс  ?
?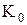 );
);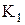 );
);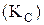 ;
; );
);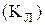 .
. . (13.1)
. (13.1) . (13.2)
. (13.2) , називаються поліномами.
, називаються поліномами.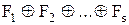 , де
, де 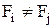 та
та 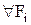 ,
, 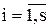 є або 1, або змінна, або кон’юнкція різних змінних, називається поліномом Жегалкіна.
є або 1, або змінна, або кон’юнкція різних змінних, називається поліномом Жегалкіна.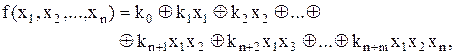 (13.3)
(13.3)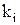 – коефіцієнти, що приймають значення 0 або 1:
– коефіцієнти, що приймають значення 0 або 1: 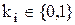 ; тобто будь-який поліном може бути перетворений у поліном Жегалкіна.
; тобто будь-який поліном може бути перетворений у поліном Жегалкіна.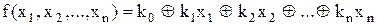 ,
, 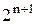 , де
, де  − число змінних, від яких залежить булева функція.
− число змінних, від яких залежить булева функція.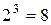 . Лінійна булева функція від двох змінних може бути зображена у вигляді полінома першого ступеня й, відповідно до формули (13.4), виражається таким способом:
. Лінійна булева функція від двох змінних може бути зображена у вигляді полінома першого ступеня й, відповідно до формули (13.4), виражається таким способом: ,
, 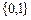 й утворюють двійкові набори, при підстановці яких у вираз (13.5) випливає вся сукупність лінійних функцій (табл. 13.1):
й утворюють двійкові набори, при підстановці яких у вираз (13.5) випливає вся сукупність лінійних функцій (табл. 13.1):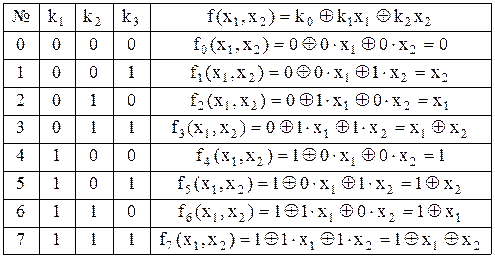
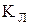 .
.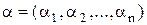 ,
, 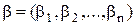 – двійкові набори,
– двійкові набори, 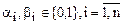 .
. передує набору
передує набору 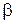 (
(  або
або  ), якщо виконується покоординатна порівнянність:
), якщо виконується покоординатна порівнянність: 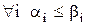 , причому хоча б для одного значення
, причому хоча б для одного значення  має місце строга нерівність
має місце строга нерівність 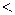 .
.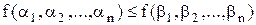 , (13.6)
, (13.6)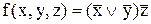 до класу монотонних.
до класу монотонних.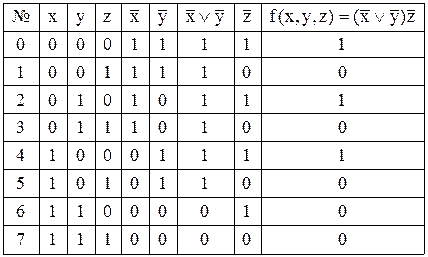


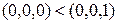 , але
, але  .
. .
.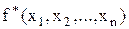 називається двоїстою для функції
називається двоїстою для функції 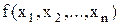 , якщо таблицю істинності для
, якщо таблицю істинності для 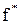 можна одержати з таблиці для
можна одержати з таблиці для 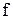 , замінивши в значеннях аргументу й функції 0 на 1 і 1 на 0, тобто має місце рівність
, замінивши в значеннях аргументу й функції 0 на 1 і 1 на 0, тобто має місце рівність . (13.7)
. (13.7) ,
, 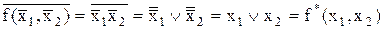 ;
;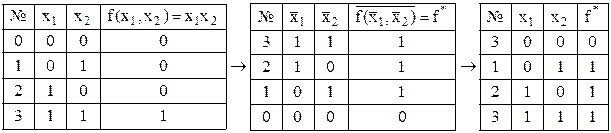
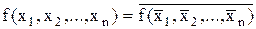 . (13.8)
. (13.8)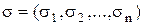 і
і  ,
, 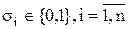 приймає протилежні значення.
приймає протилежні значення.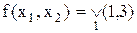 самодвоїста.
самодвоїста.
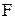 замінити знаки всіх логічних функцій на знаки двоїстих функцій, то вийде двоїста формула
замінити знаки всіх логічних функцій на знаки двоїстих функцій, то вийде двоїста формула 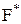 , що реалізує функцію, двоїсту тієї, яка реалізується формулою
, що реалізує функцію, двоїсту тієї, яка реалізується формулою 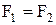 , то вірна рівність двоїстих формул
, то вірна рівність двоїстих формул 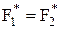 , що називається двоїстою попередній.
, що називається двоїстою попередній.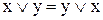 ,
, 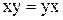 , (13.9)
, (13.9) ,
, 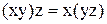 , (13.10)
, (13.10)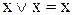 ,
, 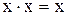 , (13.11)
, (13.11) ,
, 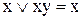 . (13.12)
. (13.12)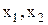
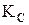
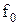
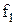
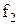
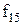
 називається функціонально повною, якщо кожна ФАЛ
називається функціонально повною, якщо кожна ФАЛ 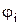 з
з 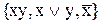 ,
, 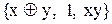 ,
, 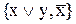 .
.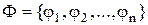 була повної необхідно й досить, щоб вона містила хоча б одну функцію, яка
була повної необхідно й досить, щоб вона містила хоча б одну функцію, яка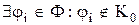 ;
;