|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Линейная комбинации строк или столбцов матрицДата добавления: 2015-08-31; просмотров: 21459; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

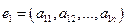 ,
, 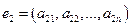 , …. ,
, …. , 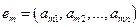
 , если
, если 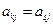 ,
, 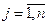 .
.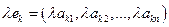 ,
,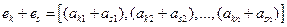
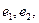 ...,
..., 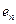 матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: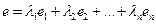 ,
, 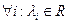 (3.2)
(3.2)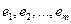 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 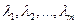 , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: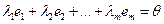 ,
, 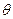 =(0,0,...,0). (3.3)
=(0,0,...,0). (3.3)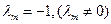 , тогда
, тогда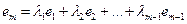 .
.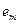 является линейной комбинат остальных строк. ■
является линейной комбинат остальных строк. ■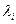 равны нулю, то строки
равны нулю, то строки 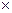 n имеет ранг r (r
n имеет ранг r (r 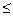 min
min 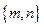 ). Это означает, что существует отличный от нуля минор r-го порядка. Всякий ненулевой минор r-го порядка будем называть базисным минором.
). Это означает, что существует отличный от нуля минор r-го порядка. Всякий ненулевой минор r-го порядка будем называть базисным минором.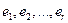 линейно независимы. Предположим противное, то есть одна из этих строк, например
линейно независимы. Предположим противное, то есть одна из этих строк, например 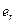 , является линейной комбинацией остальных
, является линейной комбинацией остальных 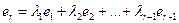 . Вычтем из элементов r - ой строки элементы 1-й строки, умноженные на
. Вычтем из элементов r - ой строки элементы 1-й строки, умноженные на 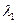 , затем элементы 2-й строки, умноженные на
, затем элементы 2-й строки, умноженные на 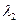 , … и элементы (r -1) - ой строки, умноженные на
, … и элементы (r -1) - ой строки, умноженные на 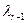 . На основании свойства 8 при таких преобразованиях матрицы ее определитель D не изменится, но так как r - я строка будет теперь состоять из одних нулей, то D = 0 - противоречие. Следовательно, наше предположение о том, что строки
. На основании свойства 8 при таких преобразованиях матрицы ее определитель D не изменится, но так как r - я строка будет теперь состоять из одних нулей, то D = 0 - противоречие. Следовательно, наше предположение о том, что строки 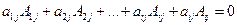 , где модуль последнего алгебраического дополнения
, где модуль последнего алгебраического дополнения 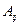 совпадает с базисным минором D и поэтому отлично от нуля, т.е.
совпадает с базисным минором D и поэтому отлично от нуля, т.е.  0.
0.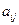 как линейную комбинацию:
как линейную комбинацию: 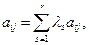 где
где 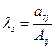 .
.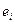 , линейно выражаются через элементы строк
, линейно выражаются через элементы строк 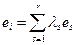 .■
.■