Школьная математика имеет дело в основном с рациональными числами.
Рациональным числом называется число вида:
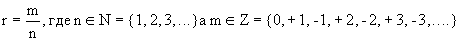
Что мы умеем делать с этими числами?
1) Складывать и вычитать:
Если 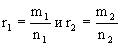 , то
, то 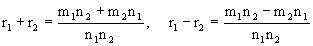
2) Умножать и делить:

3) Сравнивать:
Если 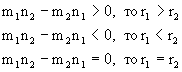
Но в связи с изучаемыми понятиями для нас нужна следующая теорема.
Теорема. Множество рациональных чисел счетно.
Доказательство.
Представим множество всех рациональных чисел в виде бесконечной таблицы.
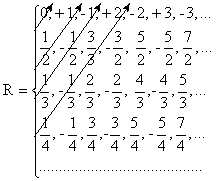
Оценим, как строятся строки этой таблицы.
Первая строка – это все целые числа, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Вторая строка – это все несократимые дроби со знаменателем 2, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Третья строка – это все несократимые дроби со знаменателем 3, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Вообще,n-ая строка это все несократимые дроби со знаменателем n, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Очевидно, что в этой таблице находятся все рациональные числа. Используя снова прием диагонализации представим R в виде:
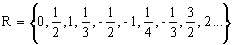
Так как R представилось в форме последовательности, то отсюда следует, что R –счетное множество. <