Пример 1.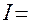 
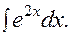
Рецепт. Вводим замену 
. Отсюда: 
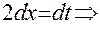(вспомним формулу дифференциала) 
. Тогда 
(обратная подстановка) 
.
Пример 2. 
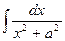
В таблице элементарных интегралов имеется формула аналогичного интеграла:
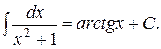Однако чаще же всего встречается более общий вариант этого интеграла: 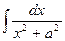, где 
─ некая числовая константа.
Рецепт. Выносим 
из знаменателя (а, значит, и из-под знака интеграла):
и делаем замену: 
. Тогда 
. А это уже знакомый табличный интеграл. Отсюда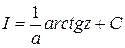 
. Проводим обратную подстановку 
и получаем в результате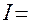 
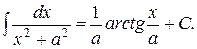
Полученным интегралом рекомендуем пополнить уже имеющуюся таблицу.
