Напомним, матрица – таблица чисел. Часто полезно рассматривать матрицу как таблицу, элементами которой являются не числа, а матрицы меньших порядков. При такой точке зрения говорят о блочном строении матрицы. Использование блочного строения матриц позволяет строить более эффективные алгоритмы.
Теорема 6.3. Умножение блочных матриц.
Пусть матрица A имеет блочное строение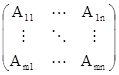 
, а матрица B имеет блочное строение 
, причем размеры блоков согласованы так, что существует произведение 
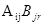при любых i,j,r. Тогда произведение матриц C=AB будет иметь блочное строение 
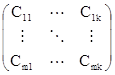, причем 
. Последнее выражение имеет такой же вид, как если бы умножали матрицы с числовыми элементами.
Доказательство. Элемент блочной матрицы A, расположенный в блоке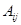 
на пересечении строки r и столбца s обозначим через 
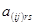. По определению произведения матриц, имеем 
, где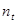 
- количество столбцов в блоке 
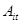(по условиям теоремы это число совпадает с количеством строк блока 
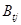). Сумма 
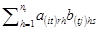является элементом матрицы 
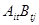, расположенным на пересечении строки r и столбца s. Следовательно, 
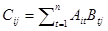, что и требовалось доказать.
Использования блочного представления матриц позволяет получать более эффективные алгоритмы для решения задач линейной алгебры.
