| Объем спроса
| Частота
| Вероятность 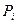
| 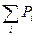
| Интервалы случайных чисел
|
|
|
| 0,05
| 0,05
| 01-05
|
|
|
| 0,1
| 0,15
| 06-15
|
|
|
| 0,2
| 0,35
| 16-34
|
|
|
| 0,3
| 0,65
| 36-65
|
|
|
| 0,2
| 0,85
| 66-85
|
|
|
| 0,1
| 0,95
| 86-95
|
|
|
| 0,05
|
| 96-00
|
Накопленная вероятность описывается интегральной функцией Лапласа.
При попадании числа в определенный интервал выбирается определенный объем спроса с определенной вероятностью.
Для решения задачи смотрим в таблицу случайных чисел, т.к. нам необходимо определить математическое ожидание 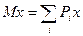 . При равновероятных событиях математическое ожидание определяется следующей формулой:
. При равновероятных событиях математическое ожидание определяется следующей формулой: 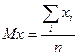 .
.
| Случайное число
| Объем спроса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
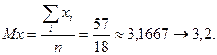
Необходимо определить точность расчетов. Предположим, что предположим, что 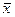 — характеристика, которая должна быть определена (в нашем случае математическое ожидание), а
— характеристика, которая должна быть определена (в нашем случае математическое ожидание), а  — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа
— ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа 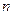 проведенных наблюдений. В этих условиях можно говорить о вероятности
проведенных наблюдений. В этих условиях можно говорить о вероятности 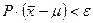 по отношению к интересующей нас характеристике
по отношению к интересующей нас характеристике 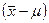 представляет собой погрешность в оценке
представляет собой погрешность в оценке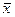 , а
, а 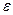 — некоторый допустимый ее предел.
— некоторый допустимый ее предел.
В нашем примере 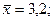
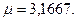
Пусть 
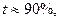
 (табличная величина);
(табличная величина); 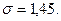
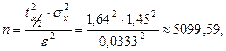
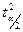 — критерий Стьюдента, количество стандартных ошибок при заданном уровне значимости
— критерий Стьюдента, количество стандартных ошибок при заданном уровне значимости 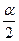 ;
;
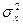 — дисперсия случайной величины
— дисперсия случайной величины 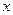 ;
;
 — несмещенная оценка.
— несмещенная оценка.