- Суть и виды статистических группировок.
- Выполнение группировки по количественному признаку.
- Ряды распределения, их виды и графическое изображение.
Суть и виды статистических группировок
В результате первой стадии статистических исследований (статистического наблюдения) получают статистическую информацию, представляющую собой большое количество первичных, разрозненных сведений об отдельных единицах объекта исследования (например, записи о каждом гражданине страны при переписи населения: пол, национальность, возраст, образование и др.).
Дальнейшая задача статистики заключается в этом, чтобы привести эти материалы в определенный порядок, систематизировать и на этой основе дать сводную характеристику всей совокупности фактов для того, чтобы изучить характерные черты и отличительные особенности изучаемого явления и выявить закономерности его развития. Это достигается на второй стадии статистического исследования, первой ступенью которой является статистическая сводка.
Статистическая сводка – это научно организованная обработка первичных данных в целях получения обобщающих характеристик изучаемого явления по ряду существенных для него признаков.
Если производится только подсчет общих итогов по изучаемой совокупности единиц наблюдения, то сводка называется простой. Например: чтобы узнать общую численность студентов высших учебных заведений Украины достаточно сложить количество студентов всех ВУЗов на определенную дату.
Статистическая сводка включает в себя такие составляющие элементы:
- выбор группировочных признаков (например, после переписи население можно делить на группы по признакам: пол, возраст, национальность);
- распределение данных на части (группы и подгруппы);
- расчет итоговых групповых данных с помощью системы статистических показателей.
- систематизация полученных результатов в виде статистических таблиц.
Объединение отдельных единиц статистической совокупности в группы осуществляется при помощи метода группировок.
Статистическая группировка – это процесс образования однородных групп по ряду существенных признаков. Осуществляется группировка либо путем деления совокупности на отдельные части, которые характеризуются внутренней однородностью и отличаются рядом признаков, либо путем объединения отдельных единиц в группы по типовым признакам (например, группировка промышленных предприятий по форме собственности, группировка населения по размеру среднедушевого дохода, группировка коммерческих банков по сумме актива баланса и т.д.).
Признаки, по которым производится распределение единиц изучаемой совокупности на группы, называются группировочными признаками или основанием группировки. Если группировка получена по количественному признаку, она называется количественной, по качественному – атрибутивной или качественной.
На группировку в статистическом анализе возлагаются следующие функции:
- выделение социально-экономических типов явлений;
- изучение структуры и структурных сдвигов;
- анализ взаимосвязей между явлениями.
В соответствии с этими функциями различают типологические, структурные и аналитические (факторные) группировки.
Типологическая группировка – это распределение качественно разнородной совокупности на классы, социально-экономические однородные типы. К этому виду относятся группировки стран по социально-политическому устройству, предприятий – по форме собственности, населения – по месту проживания (городское и сельское).
Разделение однородной совокупности на группы с целью выявления ее внутренней структуры называется структурной группировкой. Она характеризует состав совокупности, объем (весомость) ее отдельных групп.
Таблица 1 – Группировка потребителей йогурта по возрасту
Группы потребителей по возрасту, лет |
Число потребителей, чел. |
Менее 20
20-30
30-40
40-50
50-60
Старше 60 |
10
40
30
10
6
4 |
Итого |
100 |
Анализ структурных группировок, взятых за ряд периодов или моментов времени, показывает изменение структуры изучаемых явлений, т.е. структурные сдвиги, что отражает закономерности их развития.
Аналитические группировки используются для исследования наличия зависимости между изучаемыми явлениями. Для этого следует данные сгруппировать по одному из признаков, вычислить в каждой группе среднее значение второго признака, а затем сопоставить изменения изучаемых признаков. Если с увеличением или уменьшением группировочного признака увеличиваются значения второго признака, то связь (прямая или обратная) между ними существует.
Таблица 2 – Группировка магазинов по численности работников (данные условные)
Численность работников, чел. |
Количество магазинов |
Средняя фактическая продолжительность рабочей недели, ч. |
До 5 |
13 |
42,0 |
5-10 |
39 |
39,5 |
11-19 |
52 |
38,1 |
20-49 |
29 |
37,4 |
50-99 |
12 |
37,6 |
100 и более |
6 |
37,2 |
Данные показывают, что между размером предприятия и занятостью его работников существует связь: чем больше по количеству работающих магазин, тем короче рабочая неделя.
Если группы, образованные по одному признаку, делятся затем на группы по второму и т.д. признакам, то такая группировка называется комбинированной. Например, распределив группы потребителей йогурта по полу, получим комбинированную группировку.
Таблица 3 – Группировка потребителей йогурта по возрасту и полу
Группы потребителей по возрасту, лет |
Число потребителей, чел. |
всего |
в т. ч. |
мужского пола |
женского пола |
Менее 20
20-30
30-40
40-50
50-60
Старше 60 |
10
40
30
10
6
4 |
4
17
12
6
3
1 |
6
23
18
4
3
3 |
|
Итого |
100 |
43 |
57 |
|
Выполнение группировки по количественному признаку
При составлении структурных группировок на основе количественных признаков определяют количество групп и интервалы группировки.
Интервал – количественное значение, определяющее и отделяющее одну группу от другой, т.е. он очерчивает количественные границы групп.
Интервалы могут быть равные и неравные. Например: по численности работающих предприятия могут быть разбиты на группы: до 100, 100-200, 200-500, 500-1000, 1000 и более. Это объясняется тем, что изменение признака на 50-100 чел. имеет существенное значение для мелких предприятий, а для крупных – не имеет.
Для группировок с равными интервалами величина (длина, шаг) интервала определяется по формуле:
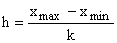 ,
,
где 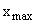 ,
,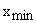 – наибольшее и наименьшее значение признака;
– наибольшее и наименьшее значение признака;
к – число групп (интервалов), определяемое по формуле Стерджесса:
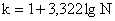 ,
,
где N – число единиц совокупности.
Округление полученных в расчетах нецелых чисел производится в большую сторону.
Например: необходимо произвести группировку с равными интервалами 20 рабочих цеха по производительности их труда. Наибольшая производительность 180 деталей за смену, наименьшая – 60.
Количество групп: 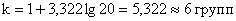
Длина интервала: 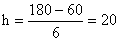 дет.
дет.
Нижняя граница 1-ой группы 60 деталей, верхняя 60+20=80 деталей. Вторая группа: нижняя граница 80, верхняя 80+20=100 и т.д. В результате получаем такой интервальный ряд (или такие группы рабочих), деталей:
1 группа: 60-80
2 группа: 80-100
3 группа: 100-120
4 группа: 120-140
5 группа: 140-160
6 группа: 160-180
В этом распределении имеется неопределенность, к какой группе отнести единицу совокупности, значение признака которой равно граничному значению интервала (рабочих с производительностью 80, 100, 200 и т. д. дет/см). Для устранения неопределенности используют принцип единообразия: левая, нижняя граница интервала включает в себя указанное значение, а верхняя – нет. Значит, рабочего, производящего 100 дет/см, относят к 3 группе.
Интервалы групп могут быть закрытыми, когда указаны верхняя и нижняя границы (как в примере), и открытыми, когда указана лишь одна из границ. Например, интервалы «менее 60» или «180 и выше» - открытые интервалы. Для расчета показателей статистической совокупности открытые интервалы необходимо «закрыть». Для этого используют величину интервала, соседнего с «открытым». В примере получим: 40-60 и 180-200.
Сказанное выше относится к группировкам, которые производятся на основе анализа первичного статистического материала. Но довольно часто приходится пользоваться уже имеющимися группировками, которые не удовлетворяют требованиям анализа. Например, группировки могут быть не сопоставимы из-за различного числа групп или неодинаковых границ интервалов. Для приведения группировок к сопоставимому виду используется метод вторичной группировки, который заключается в образовании новых групп на основе ранее осуществленной группировки. Эта перегруппировка возможна двумя способами: 1) объединением первоначальных интервалов (т.е. их укрупнением); 2) долевой перегруппировкой.
Рассмотрим пример, данные условные.
Таблица 3 – Группировка акционеров по размеру дивидендов на одну акцию.
1-й район |
2-й район |
№ груп-пы |
Группы акционеров по размеру диви-дендов, грн. |
Количество акционеров, % |
№ груп-пы |
Группы акционеров по размеру диви-дендов, грн. |
Количество акционеров, % |
1
2
3
4
5 |
1 – 4
4 – 8
8–12
12–16
16–20 |
18
12
40
25
5 |
1
2
3
4
– |
1– 6
6–12
12–20
20–30
– |
10
20
40
30
– |
|
Итого |
100 |
|
Итого |
100 |
Приведенные данные не позволяют сравнить распределение акционеров двух районов по размеру дивидендов из-за различного числа групп (5 и 4) и различной длины интервала. Взяв за основу группировку 2-го района (как более крупную), произведем вторичную группировку акционеров 1-го района.
Таблица 4 – Вторичная группировка акционеров по размеру дивидендов на 1 акцию
№ груп-пы |
Группы акционеров по размеру дивидендов, % |
Количество акционеров, % |
Расчет |
2-й район |
1-й район |
1
2
3
4 |
1 – 6
6–12
12–20
20–30 |
10
20
40
30 |
24
46
30
– |
18+0,5*12=24
0,5*12+40=46
25+5=30 |
|
Итого |
100 |
100 |
100 |
Анализ сопоставимых данных вторичной группировки позволяет сделать вывод: акционеры второго района имеют более высокие дивиденды: (12 и выше грн. получают 40+30=70 % акционеров, а в первой – только 30 %).
Ряды распределения, их виды и графическое изображение
Статистический ряд распределения – это упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку (предыдущий пример – это ряд распределения). Он, являясь разновидностью структурной группировки, характеризует состав (или структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.
Ряды распределения, построенные по атрибутивному признаку, называются атрибутивными (распределение населения по полу, занятости, профессии и т.д.).
Ряды, построенные по количественному признаку, - вариационными (распределение населения по стажу работы, з/п, возрасту.).
Конструктивно вариационный ряд распределения представляет собой таблицу, в первом столбце которой расположены варианты или их интервалы, во второй – частоты или (и) частости (третий столбец) . Принято варианты обозначать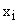 , частоты -
, частоты - 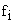 , частости -
, частости - 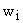 .
.
Варианты, т.е. числовые значения количественного признака в вариационном ряду распределения, могут быть положительными или отрицательными. Так, при группировке предприятий по результатам деятельности варианты положительные (прибыль) или отрицательные (убыток).
Частоты – это числа, показывающие, как часто встречаются те или варианты в данной совокупности. Сумма всех частот называется объемом совокупности и показывает число единиц совокупности, обозначается N.
Частости – это частоты, выраженные в виде относительных величин: долях единицы или в процентах, рассчитываются как отношение частоты к объему совокупности. Сумма частостей всегда равна единице или 100 %. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.
Для анализа совокупности вариационный ряд дополняют такими элементами, как накопленная частота, накопленная частость и плотность распределения.
Накопленная частота (Sf)показывает число единиц совокупности, у которых значение варианты не больше данной, определяется суммированием частот всех предшествующих интервалов, включая данный:
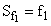 ,
, 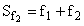 ,
,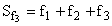 и т.д.
и т.д.
Если вместо частот использовать частости, то аналогично получим накопленные частости (Sw):
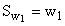 ,
, 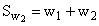 ,
, 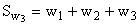 и т.д.
и т.д.
Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала, т. е. 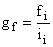 , а относительная плотность распределения – частость, приходящаяся на единицу длины интервала, т. е.
, а относительная плотность распределения – частость, приходящаяся на единицу длины интервала, т. е. 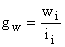 . Плотность распределения используется в рядах с неравными интервалами для приведения частот и частостей к сопоставимому виду.
. Плотность распределения используется в рядах с неравными интервалами для приведения частот и частостей к сопоставимому виду.
Вариационные ряды в зависимости от характера вариации делят на дискретные и интервальные.
Дискретные вариационные ряды строятся на основе дискретных (прерывных) признаков. Дискретные – это признаки, варианты которых имеют только целые значения и количество их невелико. Интервальные вариационные ряды основаны на непрерывных признаках (т.е. принимающих любые значения, в том числе и дробные) или дискретных, варьирующих в широком диапазоне.
Пример построения дискретного ряда распределения. Стаж работы в годах 10 рабочих бригады характеризуются следующими данными: 5, 3, 5, 4, 3, 4, 5, 4, 2, 4.
Первым шагом в упорядочении первичного ряда является его ранжирование, т.е. расположение всех вариант в возрастающем или убывающем порядке.
Ранжированный ряд: 2, 3, 3, 4, 4, 4, 4, 5, 5, 5.
Таблица 5 – Дискретный вариационный ряд распределения рабочих по стажу работы
Стаж
работы (варианты хi) |
Количество рабочих определенного стажа (частота fi) |
Частости
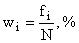 |
Накопленные частоты

|
Накопленные частости
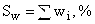
|
2
3
4
5 |
1
2
4
3 |
(1:10)*100=10
(2:10)*100=20
40
30 |
1
1+2=3
3+4=7
7+3=10 |
10
30
70
100 |
|
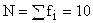
|
100 % |
- |
- |
Пример построения интервального ряда. Имеются данные о среднемесячной з/п 30 работников, которая варьируется от 600 до 1200 грн. Построить интервальный ряд распределения.
- Число интервалов (групп): к = 1+3,322 lg N = 1+3,322 lg 30 = 5,91 = 6
- Шаг интервала
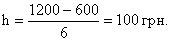
Таблица 6 – Интервальный вариационный ряд распределения рабочих по размеру среднемесячной заработной платы
Группы рабочих по размеру з/п (интервалы вариант хi) |
Количество рабочих (частоты fi ) |
Частости
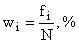
|
Накопленные частоты
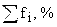 |
Накопленные частости
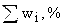 |
1) 600-700
2) 700-800
3) 800-900
4) 900-1000
5) 1000-1100
6) 1100-1200 |
3
6
8
9
3
1 |
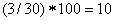 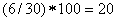 26,7 26,7
30
10
3,3
|
3
3+6=9
9+8=17
26
29
30 |
10,0
30,0
56,7
86,7
96,7
100,0 |
Итого |
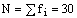
|
100 |
- |
- |
Графически ряды распределения можно представить в виде гистограммы, кумуляты, полигона.
Интервальный вариационный ряд изображают в виде гистограммы. Для ее построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, равные длине интервала. Затем на этих отрезках, как на основаниях, строят прямоугольники, высота которых пропорциональна частоте или частости. Для интервального ряда с неравными интервалами по оси ординат откладывают плотность распределения, так как в этом случае именно она дает представление о заполненности интервала. Площадь всей гистограммы численно равна сумме частот.
Пример построения гистограммы.
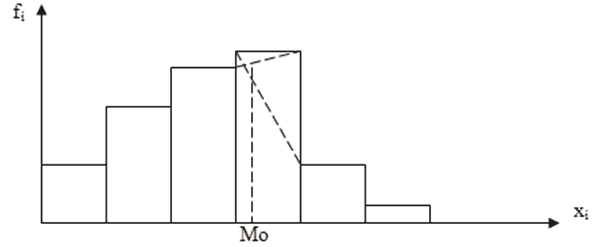
Если соединить середины каждого интервала отрезками прямой, то получим замкнутую фигуру в виде многоугольника, которая называется полигоном.
Полигон чаще используется для дискретных рядов. Для этого в прямоугольной системе координат строят точки с координатами (x1, f1), (x2, f2), …, (xN, fN), затем последовательно соединяют их отрезками, а из первой и последней точек опускают перпендикуляры на ось х. Полученный многоугольник является полигоном дискретного вариационного ряда.
Кумулята строится по накопленным частотам (или частостям), которые откладывают по оси у, а по оси х – варианты или верхние границы интервалов.


