Лемма Фаркаша

Лемма Фаркаша - утверждение выпуклой геометрии, широко используется в теории оптимизации, в частности при рассмотрении двойственных задач линейного программирования и доведение теоремы Каруша - Куна - Такера в нелинейном программировании . Лемма Фаркаша является одной из так называемых теорем альтернативности, что утверждают о существовании решения одной и только одной из немногих двух систем линейных уравнений и неравенств.

Теорема

Пусть A - матрица размерности m ? n , 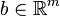$b \ in \ R ^ m$ . Тогда решение имеет только одна из таких систем:

$A x = b, \ quad x \ geq 0, \ quad x \ in \ R ^ n$
$y ^ \ top A \ leq 0, \ quad \ langle y, b \ rangle> 0 \ quad x \ in \ R ^ n$

Доказательство

Пусть система 1 имеет решение, то есть существует вектор $x \ geq 0$ такой, что A X = b . Предположим $y ^ \ top A \ leq 0,$ тогда:

$0 <\ langle y, b \ rangle = \ langle y, A x \ rangle = \ langle y ^ \ top A, x \ rangle \ leq 0$ .

Полученная противоречие доказывает, что система 2 не имеет решения.

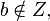Предположим, что система 1 не имеет решения. Рассмотрим замкнутую выпуклую множество $Z = \ left \ {c: c = A x, \; x \ ge 0 \ right \}$ . По предположению $b \ notin Z,$ тогда учитывая теорему о отделимость выпуклой множества и точки, что ей не принадлежит, существуют вектор $p \ in \ R ^ n, p \ neq 0$ , и число ? 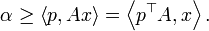такие, что $\ Left \ langle p, b \ right \ rangle> \ alpha, \ quad \; \ left \ langle p, c \ right \ rangle \ le \ alpha \ quad \ forall c \ in Z.$ Так, $0 \ in Z$ , то $\ Alpha \ geq 0, \, \ left \ langle p, b \ right \ rangle> \ alpha \ geq 0.$ С другой стороны $\ Alpha \ geq \ left \ langle p, A x \ right \ rangle = \ left \ langle p ^ \ top A, x \ right \ rangle.$ Компоненты вектора x могут быть сколь угодно большими, поэтому из последней неравенства получаем $p ^ \ top A \ leq 0.$ Таким , p - решение системы 2.