Аналитические модели и методы
Аналитические методы исследования ВС сводятся к построению математических моделей, описывающих физические свойства элементов системы математическими объектами и отношениями между ними. При использовании аналитических методов оператор 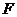 , устанавливающий зависимость
, устанавливающий зависимость 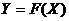 между характеристиками и параметрами системы, представляется совокупностью математических выражений. В таких моделях, называемых аналитическими, зависимость между характеристиками и параметрами может быть представлена в явной аналитической форме в виде выражения
между характеристиками и параметрами системы, представляется совокупностью математических выражений. В таких моделях, называемых аналитическими, зависимость между характеристиками и параметрами может быть представлена в явной аналитической форме в виде выражения 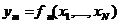 , решенных относительно искомых величин, или в неявной форме в виде уравнений
, решенных относительно искомых величин, или в неявной форме в виде уравнений 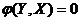 , связывающих характеристики и параметры.
, связывающих характеристики и параметры.
Как правило, свойства элементов и систем удается представить в аналитической форме, если принимаются определенные допущения о свойствах и поведении описываемых объектов: независимость одних факторов от других, линейность некоторых зависимостей, мгновенность переходов между состояниями и т.д. Если допущения соответствуют реальности, модель хорошо воспроизводит зависимость между характеристиками и параметрами. Однако, во многих случаях допущения приводят к существенным отличиям модели от реального объекта, вследствие чего моделируемая зависимость существенно отличается от реальной и характеристики представляются на модели с большой погрешностью. Так, предположение о том, что процессы обладают Марковским свойством, может оказаться ошибочным, что приводит к большим погрешностям Марковских моделей и даже к неверным оценкам. Основные аналитические методы теории массового обслуживания базируются на предположении, что интервалы времени между заявками входящих потоков и длительности обслуживания распределены по экспоненциальному закону. Когда это предположение выполняется, аналитические методы позволяют точно оценивать характеристики системы. Если же потоки и длительности существенно отличаются от предполагаемых, моделируемые характеристики могут сколь угодно отличаться от реальных.
Аналитические методы и модели составляют ядро теории ВС и ценны по следующим причинам.
- Зависимости, полученные аналитическими методами, являются строго доказанными и их достоверность не вызывает сомнений, конечно с учетом принятых при выводе допущений. Поэтому аналитические зависимости используются в качестве своеобразных эталонов, с которыми сопоставляются результаты, получаемые другими методами.
- Аналитические модели имеют большую познавательную ценность. Аналитические зависимости определяют характеристики для всей области значений параметров и несут в себе информацию о поведении соответствующих систем при любых сочетаниях параметров. На основе аналитических моделей легко определяются экстремальные и предельные значения характеристик и оцениваются эффекты от изменения параметров.
- Аналитические модели характеризуются малыми объемами вычислений. Это свойство особенно важно при решении задач синтеза, поскольку оптимизация связана с многократными вычислениями характеристик при различных значениях параметров.
Потоки заявок
Простейший поток. При аналитическом моделировании характеристики системы вычисляются наиболее просто для потока заявок, называемого простейшим. Простейший поток – это поток заявок, который обладает следующими свойствами: 1) стационарность; 2) отсутствие последействия; 3) ординарность. Стационарность означает постоянство вероятности того, что в течение определенного временного интервала поступит одинаковое количество заявок вне зависимости от расположения интервала на оси времени. Отсутствие последействия заключается в том, что поступившие заявки не оказывают влияния на будущий поток заявок, т.е. заявки поступают в систему независимо друг от друга. Ординарность – это значит, что в каждый момент времени в систему поступает не более одной заявки. Любой поток, обладающий этими свойствами, является простейшим.
У простейшего потока интервалы времени 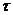 между двумя последовательными заявками – независимые случайные величины с функцией распределения:
между двумя последовательными заявками – независимые случайные величины с функцией распределения:
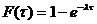 (3.1)
(3.1)
Такое распределение называется экспоненциальным (показательным) и имеет плотность
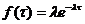 (3.2)
(3.2)
математическое ожидание длины интервала
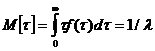 (3.3)
(3.3)
дисперсию
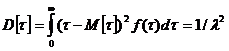 (3.4)
(3.4)
и среднеквадратическое отклонение, равное математическому ожиданию. Экспоненциальное распределение характеризуется одним количественным параметром – интенсивностью.
Простейшие потоки заявок обладают следующими особенностями:
1. Сумма 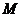 независимых, ординарных, стационарных потоков с интенсивностями
независимых, ординарных, стационарных потоков с интенсивностями 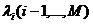 сходятся к простейшему потоку с интенсивностью
сходятся к простейшему потоку с интенсивностью
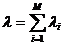 (3.5)
(3.5)
при условии, что складываемые потоки оказывают примерно одинаковое малое влияние на суммарный поток.
2. Поток заявок, полученный в результате случайного разрежения исходного стационарного ординарного потока, имеющего интенсивность 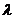 , когда каждая заявка исключается из потока с определенной вероятностью
, когда каждая заявка исключается из потока с определенной вероятностью 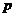 независимо от того, исключены другие заявки или нет, образует простейший поток с интенсивностью
независимо от того, исключены другие заявки или нет, образует простейший поток с интенсивностью 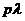 .
.
3. Интервал времени между произвольным моментом времени и моментом поступления очередной заявки имеет экспоненциальное распределение с таким же математическим ожиданием 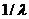 , что и интервал времени между двумя последовательными заявками.
, что и интервал времени между двумя последовательными заявками.
4. Простейший поток создает тяжелый режим функционирования системы, поскольку, во-первых, большое число (63%) промежутков времени между заявками имеет длину меньшую, чем ее математическое ожидание 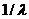 , и, во-вторых, коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию:
, и, во-вторых, коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию: 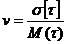 и характеризующий степень нерегулярности потока, равен единице, в то время как у детерминированного потока коэффициент вариации
и характеризующий степень нерегулярности потока, равен единице, в то время как у детерминированного потока коэффициент вариации 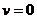 , а для большинства законов распределения
, а для большинства законов распределения 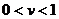 .
.
Простейший поток имеет широкое распространение не только из-за аналитической простоты связанной с ним теории, но и потому, что большое количество реально наблюдаемых потоков статистически не отличимы от простейшего. Этот эмпирический факт подтвержден рядом математических моделей, в которых при довольно общих условиях доказывается, что поток близок к простейшему.
Пуассоновский поток. Пуассоновским потоком называется ординарный поток заявок с отсутствием последействия, у которого число заявок, поступивших в систему за промежуток времени 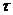 , распределено по закону Пуассона:
, распределено по закону Пуассона:
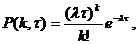
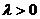 (3.6)
(3.6)
где 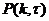 - вероятность того, что за время
- вероятность того, что за время 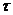 в систему поступит точно
в систему поступит точно 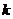 заявок;
заявок; 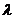 - интенсивность потока заявок.
- интенсивность потока заявок.
Математическое ожидание и дисперсия распределения Пуассона равны 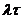 .
.
Следует подчеркнуть, что распределение Пуассона дискретно. Стационарный пуассоновский поток является простейшим. Если нестационарный поток, интенсивность которого представляет собой функцию времени 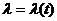 , описывается законом распределения Пуассона, то такой поток называется пуассоновским, но не простейшим. В распределении Пуассона длительности интервалов между двумя последовательными заявками – это случайные величины с экспоненциальным распределением.
, описывается законом распределения Пуассона, то такой поток называется пуассоновским, но не простейшим. В распределении Пуассона длительности интервалов между двумя последовательными заявками – это случайные величины с экспоненциальным распределением.
См. также:

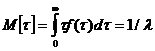 (3.3)
(3.3)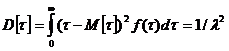 (3.4)
(3.4)