Исчисление предикатов

Слово "логика" означает систематический метод рассуждений. Рассмотрим две конкретные системы логики - базисную (исчисление высказываний) и более богатую (исчисление предикатов). Исчисление высказываний - совокупность правил, используемых для определения истинности или ложности некоторой комбинации высказываний. В логике разработаны хорошо определенные и понятные формализмы для представления фактов и правил.

Можно рассматривать предложения или высказывания обыденной разговорной речи, и с помощью исчисления производить элементарные рассуждения.

Высказывание, или предложение, или факт - это просто утверждение, которое может быть истинно или ложно. Примеры предложений:

ЕСЛИ Смит является специалистом по ЭВМ, ТО Смит – оптимист.

СМИТ является специалистом по ЭВМ.

Из этих правил можно сделать вывод:

Смит – оптимист.

Более формально выразим это, применив запись:

ЕСЛИ Р то Q, P СЛЕДОВАТЕЛЬНО Q

где P и Q предыдущие правила. Обнаружив совпадение, человек может утверждать, что суждение имеет некоторую приемлемую логическую структуру, и следовательно, может сделать вывод о том, что заключение

Смит - -оптимист

справедливо. Полностью утверждение выглядит следующим образом:

ЕСЛИ Смит является специалистом по ЭВМ, ТО Смит – оптимист.

СМИТ является специалистом по ЭВМ.

СЛЕДОВАТЕЛЬНО

Смит – оптимист.

На обоснованности примера никак не сказывается, имеет ли содержание утверждения какой-либо смысл в реальном мире. Например, следующее утверждение справедливо, хотя и абсурдно:

ЕСЛИ Смит является специалистом по ЭВМ, ТО Смит – спит.

СМИТ является специалистом по ЭВМ.

СЛЕДОВАТЕЛЬНО

Смит – спит.

Факты можно переписать в виде предикатов:

является (смит, специалист по ЭВМ)

является (смит, оптимист)

является (смит, спящий)

Эти факты выражают единичные отношения, указанные слева от скобок, и перечисленные в скобках некоторые объекты, связываемые данным соотношением.

В исчислении предикатов именами отношений соответствует термин предикаты, а объектам – аргументы. Порядок аргументов должен всегда задаваться в соответствии с интерпретацией предиката, принятой в рамках предметной области. Предикат может иметь произвольное число аргументов. Отдельные высказывания могут объединятся в сложные высказывания с помощью логических отношений И (and, &), ИЛИ (or, V), НЕ(not, ~) и импликация (-->). Использованный выше метод вывода носит латинское название modus ponens (модус поненс или сокращение утверждения). Его можно записать следующим образом:

Если истинно А и истинно А --> В, то можно вывести В.

Знак --> импликация (произносится влечет) применяется для формирования правил и читается «ЕСЛИ ...., ТО ......». Таким образом, из двух данных предложений можно вывести третье.

Некоторый объект может быть представлен как константа, т.е. как конкретный индивидуум, или как переменная, например:

является (Х, специалист по ЭВМ).

Когда переменной ставится в соответствие определенное имя некоторого объекта, т.е. некоторой константы, происходит порождение экземпляра этой переменной. Здесь все константы начинаются со строчной буквы. Для того чтобы в исчислении предикатов можно было манипулировать переменными, потребовалось ввести дополнительную структуру- квантор.

Кванторы служат для указания меры, в какой экземпляры переменных должны быть истинными, для того чтобы в целом высказывание стало истинным. Различают квантор общности, обозначаемый символом 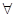- квантор общности, который означает "для каждого" или "для всех", и квантор существования, которому соответствует символ .

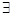Квантор 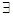применяется, когда нужно сказать, что существует хотя бы одно некоторое значение переменной, для которой истинно данное утверждение.

Если применяется квантор общности, то говорят, что утверждение истинно для всех X в некотором множестве. Иными словами, если подставить вместо X любое значение, то утверждение будет истинно.

Если в утверждение входят несколько кванторов, то приходится учитывать их взаимное расположение.

Пользуясь кванторами, можно представить предложение:

Все специалисты по ЭВМ является программистами.

следующим образом:

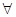(X) специалист по ЭВМ (X) -->программист(X).

Предложение

Некоторые специалисты по ЭВМ является оптимистами.

может быть представлено так:

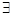(X) специалист по ЭВМ (X) -->оптимист(X).

Порядок, в соответствии с которым вводятся квантифицируемые переменные, может влиять на смысл утверждения: Например, выражение

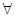(X) 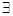(Y) служащий (X) -->руководитель(Y,X).

Может быть интерпретировано так:

У каждого служащего есть руководитель.

Если же изменить порядок следования кванторов, например

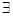
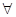(X) 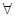(Y) служащие (X) -->руководитель(Y,X).

то изменится и утверждение

Есть такое лицо, которое руководит всеми.

В исчислении предикатов существует много различных правил вывода. Они могут применятся либо для установления истинности утверждения в целом, либо для порождения заключения. Вот некоторые правила вывода:

Modus ponendo ponens (MPP): A--> B, A ? B (? означает "верно, что "или "имеет место").
Modus tollendo tollens (MTT): A--> B, ~A ? ~B (например ЕСЛИ моя программа правильна, ТО она будет работать, моя программа НЕ будет работать, СЛЕДОВАТЕЛЬНО, она не правильна).
Двойное отрицание (ДО): ~A ? ~(~ B) (например, моя программа работала СЛЕДОВАТЕЛЬНО, моя программа НЕ НЕ работала).
Введения конъюнкции (ВК): А, B ? {A & B} (например, моя программа работала, она правильна, СЛЕДОВАТЕЛЬНО, моя программа работала И она правильна).
Reductio ad absurdum (RAA): A--> B, A--> ~ B ? ~A (например, ЕСЛИ моя программа правильна, ТО она будет работать, ЕСЛИ моя программа правильна ТО она не будет работать, СЛЕДОВАТЕЛЬНО, моя программа не правильна).
Специализации (С): 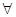(X) W(X), A ? W(X) (например, все предметы, являющимися компьютерами, не надежны, «TIPTOP»- компьютер, СЛЕДОВАТЕЛЬНО, «TIPTOP» ненадежен).

Раскрывая скобки и приводя подобные члены, всегда можно привести формулу исчисления высказываний к одной из двух форм:

Конъюнктивная нормальная форма. Формула записана в виде конъюнкции дизъюнктов (С1 И С2 И... СN). Каждый дизъюнкт является дизъюнкцией атомарных предложений или отрицаний таких предложений (Р1 ИЛИ НЕ Р2 ИЛИ ... РМ). Это помогает в рассуждениях, так как истинность всей формулы означает истинность каждого дизъюнкта в отдельности, что облегчает рассмотрение формулы.
Дизъюнктивная нормальная форма. Формула записана в виде дизъюнкции выражений, каждое из которых является конъюнкцией атомарных предложений или их отрицаний. В такой форме часто бывает удобно записывать булевы выражения, описывающие переключательные схемы или условия наступления каких-либо событий. Пусть, например, мы хотим написать, что два члена комитета, состоящего из трех человек (Андерсон, Бейнс и Кларк), голосовали за некоторое предложение, а один голосовал против. Мы можем символически записать "Андерсон голосовал "за" в виде А, "Бейнс голосовал "за"- в виде В, и "Кларк голосовал против" в виде "НЕ С". Выражая эту возможность и две остальные в виде составного предложения в дизъюнктивной нормальной форме, можно написать

(А И В И НЕ C) ИЛИ (НЕ А И В И С) ИЛИ (А И С И НЕ В).

Каждое из выражений в скобках истинно лишь при одной конкретной комбинации значений А, В и С. Для любых значений А, В и С, отличных от этих комбинаций, все выражения в скобках будут ложными, так что и формула в целом будет ложной. Таким образом, если эта формула верна для голосования в комитете, то утверждения А, В, С не могут быть одновременно истинны, не могут быть одновременно ложны и более чем одно из них не может быть ложным.