Из правых собственных векторов можно составить матрицу T , а из левых – матрицу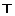 
, которые обладают уникальными свойствами по отношению к матрице A.
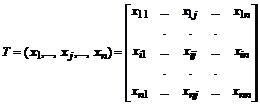
Умножив матрицу A слева на матрицу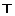 
, а справа - на матрицу T , после несложных преобразований получим:
.
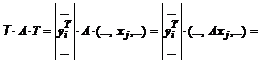
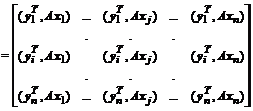Каждое скалярное произведение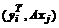 
в матрице, принимая во внимание линейную независимость собственных векторов, полученных для различных собственных значений, можно преобразовать так:
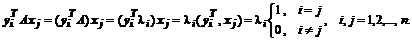
Поэтому, результатом преобразования матрицы A будет диагональная матрица с собственными значениями, расположенными на диагонали:
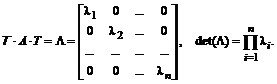
Если вместо A взять единичную матрицу и проделать аналогичные преобразования, то станет очевидным равенство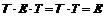 
, откуда следует 
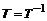. Последнее позволяет для преобразования матрицы A в диагональную обходиться только системой правых собственных векторов-столбцов:
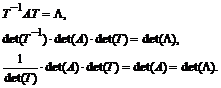
Последнее показывает, что умножение матрицы A на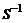 
слева и на S справа, где S - произвольная не особая матрица, преобразует ее в некоторую матрицу B , которая имеет определитель, равный определителю матрицы A . Такие преобразования матриц называют эквивалентными (подобными).
Продолжая использовать T-матрицу, несложно получить следующие важные результаты:
.
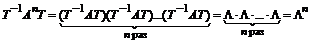