Используя разностную аппроксимацию пространственной переменной и сохраняя непрерывное время, решить уравнение теплопроводности, описывающее динамику нагрева металлического стержня из алюминия, на концах которого поддерживается заданный закон изменения температуры.
Изменение температуры 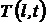 в теплоизолированном стержне постоянного сечения и длиной L метров (
в теплоизолированном стержне постоянного сечения и длиной L метров (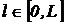 ) описывается дифференциальным уравнением в частных производных
) описывается дифференциальным уравнением в частных производных
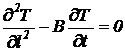 .
.
На концах стержня задано изменение температуры во времени функциями 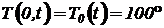 и
и 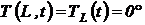 . В начальный момент распределении температуры по длине равно
. В начальный момент распределении температуры по длине равно 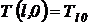 .
.
Постоянный коэффициент уравнения связан с тепловыми и массовыми константами материала стержня следующим образом:
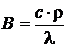 ,
,
где 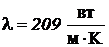 - теплопроводности алюминия при
- теплопроводности алюминия при 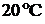 ;
;
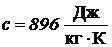 - удельная теплоемкость алюминия при
- удельная теплоемкость алюминия при 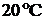 ;
;
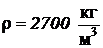 - плотность алюминия.
- плотность алюминия.
Аппроксимация дифференциальными уравнениями
Введем в исходное уравнение относительные переменные для температуры и длины, умножив и разделив соответствующие переменные на их максимальные значения, и обозначим так:
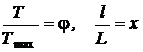 .
.
В относительных переменных уравнение запишем в виде:
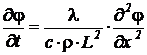
При длине стержня L=0,1 м коэффициент перед второй частной производной (коэффициент температуропроводности деленный на квадрат длины стержня) для алюминия равен
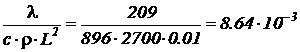 .
.
Стержень единичной длины разделим на 8 равных частей с шагом 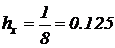 и обозначим значение относительной температуры в каждой точке индексной переменной
и обозначим значение относительной температуры в каждой точке индексной переменной 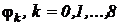 .
.
Применим трех точечную аппроксимацию частной производной второго порядка, воспользовавшись таблицей 4.
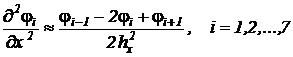 .
.
Удвоенный квадрат шага по длине стержня, стоящий в знаменателе, равен 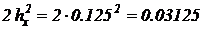 . Коэффициенты в числителе для внутренних и приграничных точек одинаковые.
. Коэффициенты в числителе для внутренних и приграничных точек одинаковые.
Подставим в исходное уравнение конечно-разностное выражение частной производной и обыкновенную производную по времени, в результате чего получим систему обыкновенных дифференциальных уравнений первого порядка:
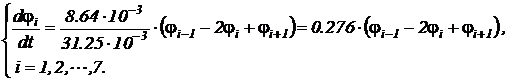 .
.
В развернутом виде: 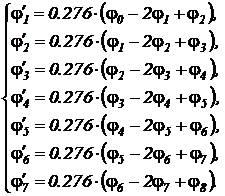
В полученной системе значения относительной температуры на границе равны 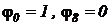 . Начальное распределение
. Начальное распределение 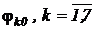 .
.
Соотношение между шагом по временной переменной 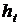 и по пространственной
и по пространственной 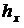 должно подчиняться следующему неравенству:
должно подчиняться следующему неравенству: 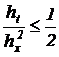 . Для данной задачи квант времени
. Для данной задачи квант времени 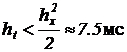 . Нарушение условия может вызвать численную неустойчивость при решении.
. Нарушение условия может вызвать численную неустойчивость при решении.
Вычислительная модель системы
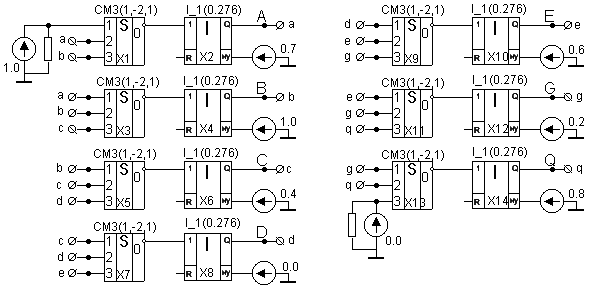
Выберем диапазон изменения машинных переменных равный диапазону изменения относительных переменных, т.е. 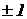 В. В этом случае масштабные множители всех относительных переменных будут равны единице, а коэффициенты по входам сумматоров - коэффициентам при переменных в уравнениях. Схема соединения операционных блоков для этой задачи показана на рисунке 66.
В. В этом случае масштабные множители всех относительных переменных будут равны единице, а коэффициенты по входам сумматоров - коэффициентам при переменных в уравнениях. Схема соединения операционных блоков для этой задачи показана на рисунке 66.
Рисунок 66
Решение задачи методом моделирования
Для получения конкретных решений зададим некоторый вектор начального распределения относительной температуры по длине стержня, например:
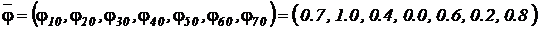 .
.
Существенные изменения температур на всей длине стержня должны происходить на протяжении не менее четырех постоянных времени. Эта постоянная в данной задаче равна обратной величине от константы, стоящей перед скобками: 1/0,276=3,62. Поэтому время развертки переходных процессов установим 20 секунд.
Результаты решения представлены на рисунке 67.
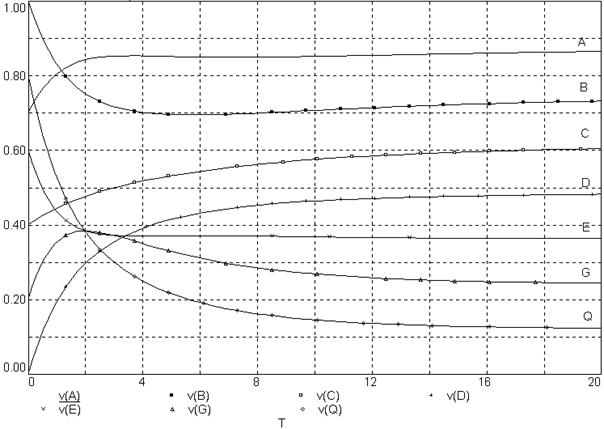
Рисунок 67
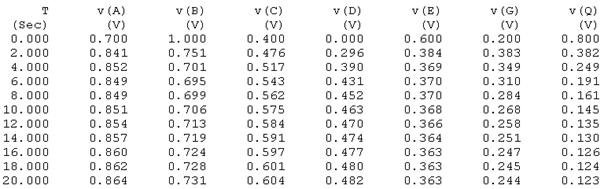
Числовые значения кривых для нескольких временных сечений приведены в таблице 8.
Таблица 8.-Численное представление результатов моделирования
Кривые Q, G, E, D, C, B, A представляют соответственно изменения относительных температур 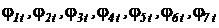 во внутренних точках стержня. На графике видно стремление кривых к известному установившемуся решению, а именно: равномерное ступенчатое понижение температуры от 100 градусов до нуля.
во внутренних точках стержня. На графике видно стремление кривых к известному установившемуся решению, а именно: равномерное ступенчатое понижение температуры от 100 градусов до нуля.
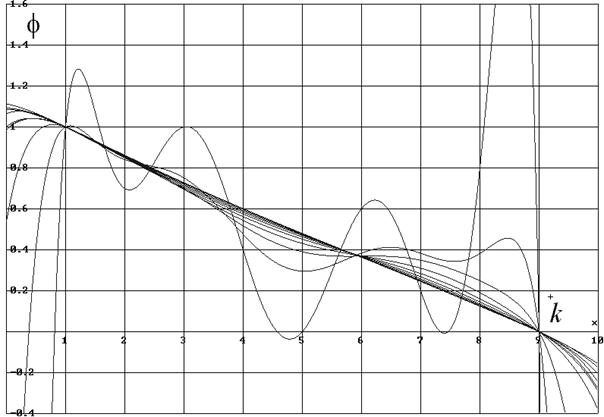
Рисунок 68. Распределение температуры во временных сечениях.
Если через 9 точек каждого временного сечения провести кривые интерполирующих многочленов 8-й степени, то графики этих кривых, приведенные на рисунке 68, очевидным образом выявят их стремление к прямой линии, соединяющей точки концевых значений относительной температуры.
Текстовую таблицу 8, формируемую пакетом Micro-Cap V, после несложного преобразования в формат представления матриц в математических пакетах (например, в DERIVE версий выше 4.02), можно использовать для построения таких интерполирующих многочленов с последующим их отображением в графической форме (Рис.68). Пример программы такой обработки текстового файла в операторах DERIVE приведен в конце этого раздела.
Решение задачи методом аналогий
Трех точечная аппроксимация второй частной производной по пространственной переменной приводит к системе уравнений, которые по форме записи совпадают с записью первого закона Кирхгофа для линейных электрических цепей. Это легко заметить, если каждое дифференциальное уравнение системы преобразовать по Лапласу и разрешить относительно переменной с центральным индексом, то получим систему следующего вида:
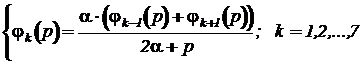 ,
,
где 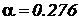 - ранее вычисленный коэффициент;
- ранее вычисленный коэффициент;
p - комплексный параметр, вызванный применением
преобразования Лапласа к производной.
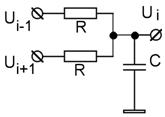
Рисунок 69 |
Аналогичное выражение получается для напряжений в пассивной электрической цепи, показанной на рисунке 69, если для входных и выходных напряжений использовать одинаковую индексацию.
Зависимость напряжения на внутреннем узле по отношению к общему проводу будет:
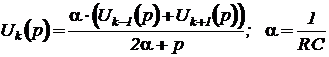 .
.
Если положить равными 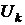 и
и 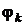 , то для емкости С=1 мкФ сопротивления будут равны
, то для емкости С=1 мкФ сопротивления будут равны 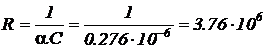 Ом.
Ом.
Соединив семь таких ячеек (аналогов семи дифференциальных уравнений системы) в последовательную электрическую цепь, мы получаем аналоговую модель дифференциального уравнения теплопроводности, которая изображена на рисунке 70.
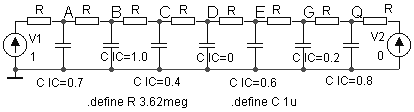
На концевые входы последовательной RC-цепи подключены источники напряжений с напряжениями 0 и 1 вольт, имитирующие холодный и нагретый конец стержня.
Рисунок 70
Перед началом решения каждый конденсатор зарядим до напряжения, соответствующего начальному распределению температуры по стержню. Для удобства сопоставления решений различными методами все начальные значения температуры и обозначения узловых точек сохраним прежними.
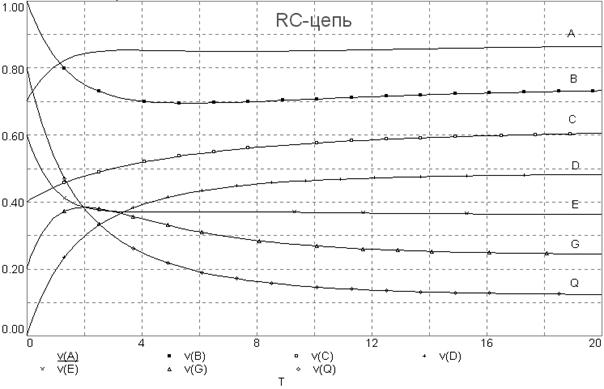
Графики решения задачи методом аналогий представлены на рисунке 71.
Рисунок 71
Решения задачи двумя методами, оказались практически идентичными. Затраты на подготовку к моделированию в среде виртуальной гибридной вычислительной машины свелись к построению схем соединения операционных блоков и заданию их параметров.
Самой громоздкой частью процесса решения задачи в частных производных, независимо от применяемых вычислительных средств, является построение аппроксимирующей математической модели.
Пример программы построения интерполирующих многочленов в математическом пакете DERIVE v(4-5) (см. раздел 5.3) применительно к таблице результатов решения уравнения теплопроводности.

После выполнения оператора 9 программа выводит матрицу с одним столбцом, каждая строка которого представляет полином восьмой степени. Используется процедура метода наименьших квадратов (оператор FIT) с максимально возможной степенью полинома.

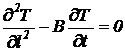 .
.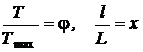 .
.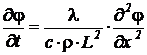
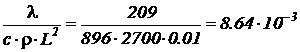 .
.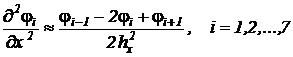 .
.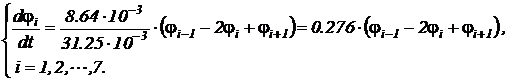 .
.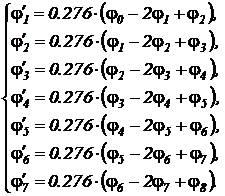
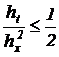 . Для данной задачи квант времени
. Для данной задачи квант времени 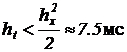 . Нарушение условия может вызвать численную неустойчивость при решении.
. Нарушение условия может вызвать численную неустойчивость при решении. 



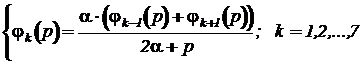 ,
,
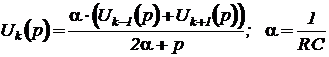 .
.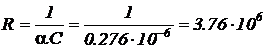 Ом.
Ом. 

