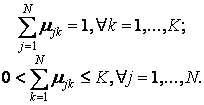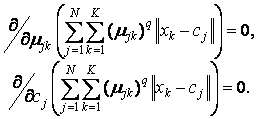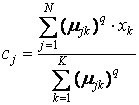FCM-алгоритм кластеризації
Алгоритм нечіткої кластеризації називають FCM-алгоритмом (Fuzzy Classifier Means, Fuzzy C-Means). Метою FCM-алгоритму кластеризації є автоматична класифікація безлічі об'єктів, які задаються векторами ознак в просторі ознак. Іншими словами, такий алгоритм визначає кластери і відповідно класифікує об'єкти. Кластери представляються нечіткими множинами, і, крім того, кордони між кластерами також є нечіткими.
FCM-алгоритм кластеризації припускає, що об'єкти належать всім кластерах з певною ФП. Ступінь приналежності визначається відстанню від об'єкту до відповідних кластерних центрів. Даний алгоритм ітераційно обчислює центри кластерів і нові ступеня приналежності об'єктів.
Для заданого безлічі вхідних векторів хk і N виділюваних кластерів j передбачається, що будь-який хк належить будь-якому j з належністю µjk інтервалу [0,1], де j - номер кластеру, а k - номер вхідного вектора.
Приймаються до уваги наступні умови нормування для µjk:
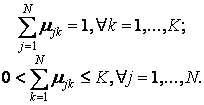
Мета алгоритму - мінімізація суми всіх зважених відстаней 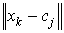 :
:
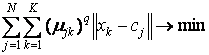 ,
,
де q - фіксований параметр, ставиться перед ітерації.
Для досягнення цієї мети необхідно вирішити таку систему рівнянь:
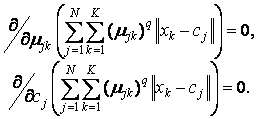
Спільно з умовами нормування µjk дана система диференціальних рівнянь має наступне рішення:
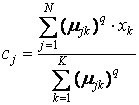
(зважений центр гравітації) і

Алгоритм нечіткої кластеризації виконується по кроках
Крок 1. Ініціалізація.
Вибираються наступні параметри:
• необхідну кількість кластерів N, 2 < N < ;
• міра відстаней, як Евклидово відстань;
• фіксований параметр q (зазвичай 1,5);
• початкова (на нульовий ітерації) матриця приналежності 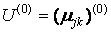 об'єктів хk з урахуванням заданих початкових центрів кластерів j.
об'єктів хk з урахуванням заданих початкових центрів кластерів j.
Крок 2. Регулювання позицій 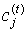 центрів кластерів.
центрів кластерів.
t-м итерационном кроці при відомій матриці 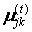 обчислюється
обчислюється 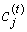
Крок 3. Коригування значень приналежності µjk.
Враховуючи відомі 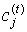 , обчислюються
, обчислюються 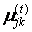 , якщо
, якщо 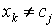 , інакше:
, інакше:
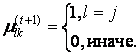
Крок 4. Зупинка алгоритму.
Алгоритм нечіткої кластеризації зупиняється при виконанні наступного умови:
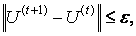
де|| || - матрична (норманаприклад, Евклідового норма);
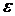 - заздалегідь заданий рівень точності.
- заздалегідь заданий рівень точності.
Рішення завдань кластеризації
Існують два способи вирішення завдань кластеризації у Matlab: з використанням командного рядка або графічного інтерфейсу користувача. Розглянемо перший із зазначених способів.
Для знаходження центрів кластерів в Matlab є, вбудована функція fcm, опис якій представлено нижче.
Опис функції:
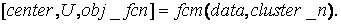
Аргументами цієї функції є:
1) data - безліч даних, що підлягають кластеризації, кожен рядок описує крапку в багатовимірному просторі характеристик;
2) cluster_n - кількість кластерів (більше одного).
Функцією повертаються наступні параметри:
1) center - матриця центрів кластерів, кожен рядок якої містить координати центру окремого кластера;
2) U - результуюча матриця ФП;
3) obj_fcn - значення цільової функції на кожній ітерації.
Приклад П11. Програма нечіткої кластеризації.
// завантаження даних, що підлягають кластеризації, з файлу
load fcmdata.dat;
// визначення центру кластеризації (два кластера)
[center, U, obj_fcm] = fcm( fсmdata, 2);
// визначення максимального ступеня приналежності
// окремого елемента даних кластеру
maxU = max(U);
// розподіл рядків матриці даних між відповідними
// кластерами
index1 = find (U(1, :) == maxU);
index2 = find(U(2, :) = maxU);
// побудова даних, відповідних першому кластеру
plot (fcmdata (index1, 1), fcmdata (index1, 2)," ko", "markersize", 5, "LineWidth" ,1);
hold on
// побудова даних, відповідних другого кластеру
plot(fcmdata (index2, 1), fcmdata(index2, 2), "kx", "markersize", 5, "LineWidth", 1);
// побудова кластерних центрів
plot(center(1, 1), center(1, 2), "ko", "markersize", 15", LineWidth", 2)
plot (center (2, 1), center (2, 2), "kx", "markersize", 15, "LineWidth", 2)
На рис. П15 представлено безліч даних, що підлягають кластеризації та знайдені центри кластерів для прикладу П.11.
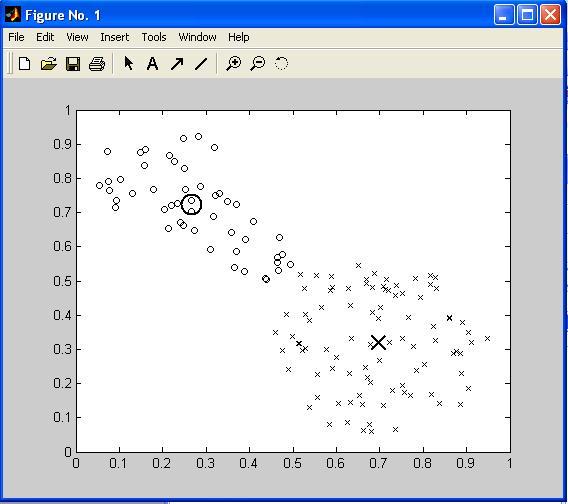
пРис. П15. Безліч аналізованих даних і центри кластерів
Функція fcm виконується ітераційно до тих пір, поки зміни цільової функції перевищують деякий заданий поріг. На кожному кроці в командному вікні Маtlab виводяться порядковий номер ітерації і поточне значення цільової функції.
Номер ітерації |
Значення цільової функції |
Номер ітерації |
Значення цільової функції |
1 |
8,94 |
7 |
3,81 |
2 |
7,31 |
8 |
3,8 |
3 |
6,9 |
9 |
3,79 |
4 |
5,41 |
10 |
3,79 |
5 |
4,08 |
11 |
3,79 |
6 |
3,83 |
12 |
3,78 |
Для оцінки динаміки зміни значень цільової функції використовується команда побудови графіка plot(obj_fcm). Результати прикладу П11 показані на мал. П16.
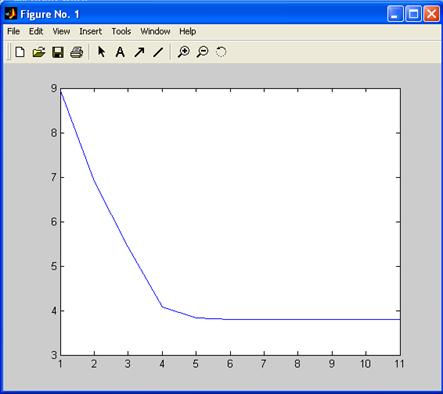
Рис. П16. Графік зміни значень цільової функції
Функцію кластеризації можна викликати з додатковим набором параметрів: fcm (data, cluster_n, options). Додаткові аргументи використовуються для управління процесом кластеризації:
• options(1) - показник ступеня для матриці U (за умовчанням - 2.0);
• options(2) - максимальна кількість ітерацій (за умовчанням - 100);
• options(3) - граничне зміна значень цільової функції (за умовчанням - 1е-5);
• options(4) - відображення інформації на кожному кроці (за замовчуванням - 1).
Приклад визначення функції fcm з додатковими параметрами:
[center, U, obj_fcn] = fсm(fcmdata, 2, [2,100,le-5,1]).
Другий спосіб вирішення завдань кластеризації Matlab заснований на використанні ГИП, який викликається командою findcluster. Головне вікно інструменту кластеризації показано на рис. П17.
Кнопка <Load Data> використовується для завантаження підлягають кластеризації вихідних даних наступного формату: кожен рядок являє собою крапку в багатовимірному просторі характеристик, кількість рядків відповідає кількості точок (елементів даних). Графічну інтерпретацію вихідних даних можна спостерігати в однойменному вікні головного вікна інструменту.
Вибір типу алгоритму кластеризації здійснюється з використанням випадного меню Methods (пункт меню - fcm). Далі визначаються параметри алгоритму кластеризації:
• кількість кластерів (рядок - Cluster Num);
• максимальна кількість ітерацій (рядок - Мах Iteration#);
• мінімальне значення поліпшення цільової функції (рядок - Min. Improvement);
• показник ступеня при матриці ФП (рядок - Exponent).
Після визначення необхідних значень, зазначених параметрів здійснюється запуск алгоритму кластеризації з допомогою кнопки <Start>. Кількість вироблених ітерацій і значення цільової функції можна переглянути в нижній частині головного вікна інструменту кластеризації.
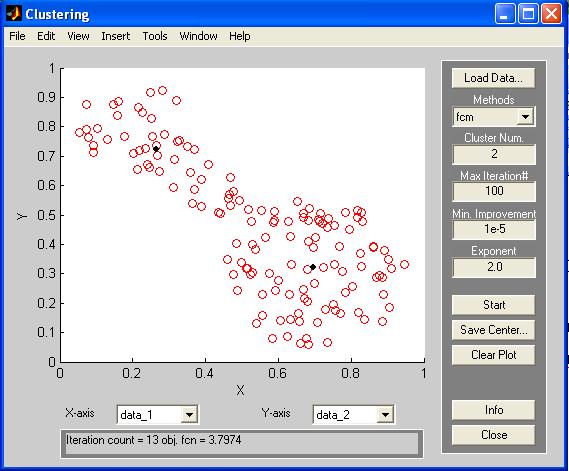
Рис. П17. Головне вікно кластеризації у Matlab
Координати знайдених центрів кластерів можна зберегти, клацнувши мишею по кнопці <Save Center...>. Кожен рядок матриці у файлі являє собою набір координат окремого кластеру. Кількість рядків відповідає кількості кластерів.