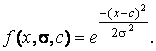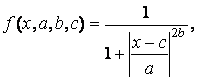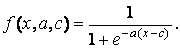Функції належності
Інструментарій нечіткої логіки (ІНЛ) у складі пакету Matlab містить 11 вбудованих типів функцій належності (ФП), що формуються на основі кусково-лінійних функцій, розподілу Гаусса, сигмоидной кривий, квадратичних і кубічних поліноміальних кривих. До найбільш простим ФП можна віднести трикутну і трапецієподібну. Найменування трикутної ФП - trimf (triangle membership function). В параметричного вигляді вона являє собою не що інше, як набір трьох точок, які утворюють трикутник.
Опис функції:= trimf(x, [ab]),
де вектор х - базове безліч, на якому визначається ФП. Величини і задають підстава трикутника, b- його вершину.
пВ аналітичному вигляді трикутна ФП може бути задана наступним чином (мал. П1, а):
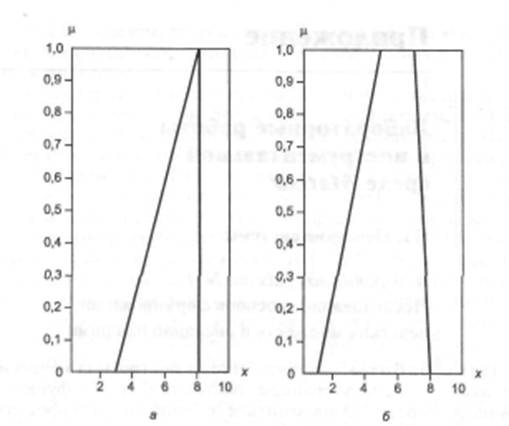
Рис. П1. Трикутна () і трапецієвидна (в) функції приналежності
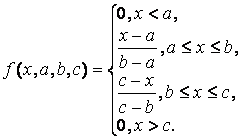
Далі розглянемо приклади використання різних ФП у системі.
Приклади являють собою фрагменти програм і коментарів мовою пакету Matlab.
Приклад П1. Програма використання ФП trimf
х = 0 : 0,1 : 10; Задається базове безліч
= trimf(x, [3 6 8]); Визначається трикутна ФП
plot (х, у) ; Виводиться графік функції
xlabel("trimf(x, P), P = [3 6 8]"); Підписується графік під віссю абсцис
Трапецієподібна ФП - trapmf (trapezoid membership function) - відрізняється від попередньої функції лише тим, що має верхнє підставу.
Опис функції: = trapmf(х, [abс d]),
де параметри і d - нижня основа трапеції;
bі -верхнє підстава трапеції (мал. П1, б).
Аналітична запис трапецієподібної функції має вигляд:
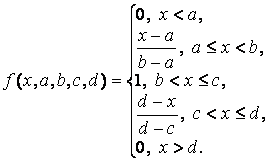
Одна з основних переваг трикутних і трапецієподібних ФП - їх простота. На основі функції розподілу Гаусса можна побудувати ФП двох видів: просту функцію приналежності Гаусса й двосторонню, утворену з допомогою різних функцій розподілу Гаусса. Перша з них позначається gaussmf, а друга - gauss2mf.
Опис функції:
= gaussmf(x, [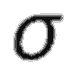 , з]).
, з]).
Симетрична функція Гаусса залежить від двох параметрів 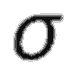 і (рис. П.2, а):
і (рис. П.2, а):
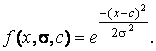
Приклад П2. Програма використання ФП gaussmf
X= 0 : 0,1 : 10;
Y= gaussmf(х, [2 5]);
plot (х, у);
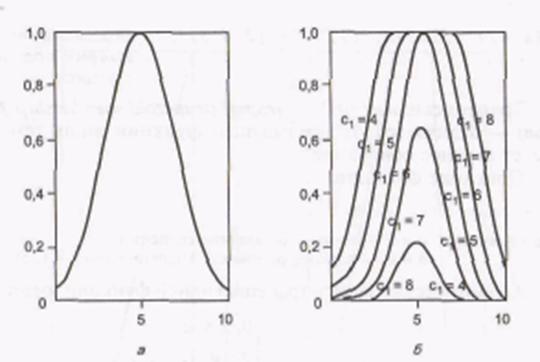
Рис. П2. Проста (а) і двостороння (б) функції належності Гаусса.
Опис функції: = gauss2mf (x, [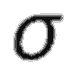 1, с1,
1, с1, 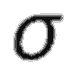 2, c2]).
2, c2]).
пПоследнее вираз є комбінацією двох різних функцій розподілу Гаусса. Перша визначається параметрами 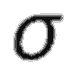 1 і с1 і задає форму лівого боку, а друга (параметри
1 і с1 і задає форму лівого боку, а друга (параметри 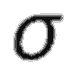 2, c2) - правою сторони ФП.
2, c2) - правою сторони ФП.
с1 < c2, то в цьому випадку функція gauss2mf досягає свого максимального значення на рівні 1. Інакше - максимальне значення функції менше 1 (рис. П2, б).
Приклад ПЗ. Програма використання ФП gauss2mf
х= (0 : 0,1 : 10)";
y1 = gauss2mf(x, [2 4 1 8]);
у2 = gauss2mf(x, [2 5 1 7]);
уЗ = gauss2mf(x, [2 6 1 6]);
у4 = gauss2mf(x, [2 7 1 5]);
У5 = gauss2mf(x, [2 8 1 4]);
Plot (x, [y1 у2 уЗ у4 у5]);
Символ «"» у рядку визначення базового безлічі х показує транспонированность базового безлічі.
пСледующей функцією, яка дозволяє представляти нечіткі суб'єктивні переваги, є ФП «узагальнений дзвін» і позначається gbellmf(generalized bell shape membership function).
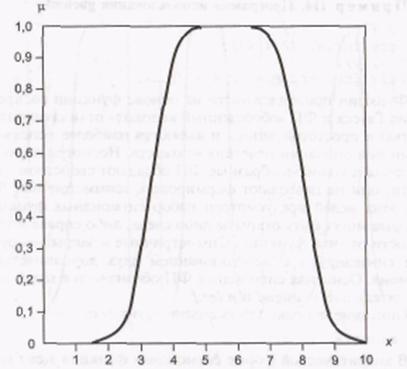
gbellmf, P = [2 4 6]
Рис. П3. Функція приналежності «узагальнений дзвін»
Її відмінність від розглянутих ФП полягає в додаванні третього параметра, що дозволяє здійснювати плавний перехід між нечіткими множинами.
Опис функції: = gbellmf (x, [а b з]) .
Функція «узагальнений дзвін» залежить від трьох параметрів і має наступну аналітичну запис:
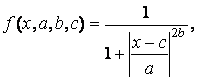
де - визначає розташування центру ФП; і b - впливають на форму кривої (мал. ПЗ).
Приклад П4. Програма використання gbellmf
х = 0 : 0,1 : 10;
= gbellmf (х, [2 4 6]);
plot(x, y);
xlabel("gbellmf, р = [2 4 61]").
Функції належності на основі функції розподілу Гаусса й ФП “узагальнений дзвін” відрізняються гладкістю і простотою запису і є найбільш використовуваними при описі нечітких множин. Незважаючи на те, що гауссовы і колоколообразные ФП володіють властивістю гладкості, вони не дозволяють формувати асиметричні ФП. Для цих цілей передбачений набір сигмоидных функцій, які можуть бути відкриті або ліворуч або праворуч в залежності від типу функції. Симетричні і закриті функції синтезують з використанням двох додаткових сигмоид. Основна сигмоидная ФП позначається sigmf, а додаткові - dsigmf і psigmf.
Опис основний сигмоидной функції: = sigmf (х, [a]з).
В аналітичній формі сигмоидная функція sigmf записується наступним чином:
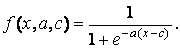
пВ залежності від знаку параметра розглянута ФП буде відкрита або праворуч або ліворуч (мал. П4, ), що дозволить застосовувати її при описі таких нечітких понять, як «дуже великий», «вкрай негативно» та ін.
Опис додаткової сигмоидной функції: = dsigmf(x, (a1, c1, а2, с2)) .
ФП dsigmf залежить від чотирьох параметрів a1, c1, а2 і с2 і визначається як різниця двох сигмоидных функцій: f(x, a1, c1) - f(x, а2, с2) (мал. П4, в).
Опис додаткової сигмоидной функції: = psigmf (x, [a1, c1, а2, с2]) .
ФП psigmf, так само як і попередня функція залежить від чотирьох параметрів a1, c1, а2, с2 і визначається як добуток двох сигмоидных функцій f(x, a1, c1)*f(x, а2, с2) (мал. П4, ).
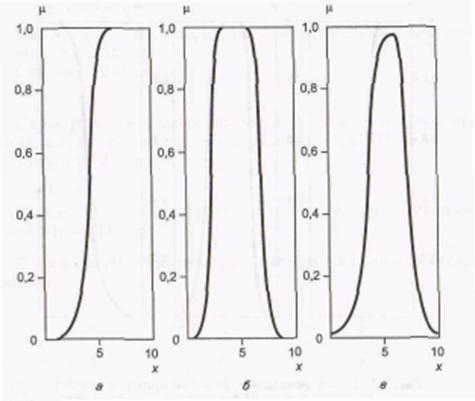
Рис. П4. Сигмоилные функції приналежності:
- основна одностороння; б - додаткова двостороння;
- додаткова несиметрична
Приклад П5. Програма використання сигмоидных функцій
х = 0 : 0,1 : 10; визначається базове безліч
subplot (1, 3, 1); формується матриця графіків (3x1)
перший елемент - поточний
y=sigmf(x,[2 4]);
plot (х, у); виводиться графік у перший елемент матриці
xlabel ("sigmf, P = [2 4]")
subplot (1, 3, 2); вибирається другий поточний елемент
= dsigmf (x, [5 2 5 7]);
plot (х, у); виводиться графік у другий елемент матриці
xlabel ("dsigmf, Р = [5 2 5 7]")
subplot (1, 3, 3); вибирається третій поточний елемент
= psigmf (x, [2 3 -5 8]);
plot (х, у); виводиться графік у третій елемент матриці
xlabel ("psigmf, P= [2 3 -5 8]");
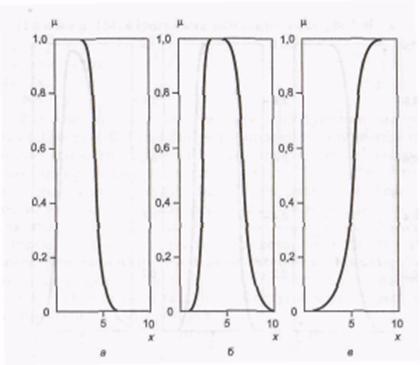
Рис. П5. Поліноміальні функції приналежності:
а - Z-функція; б - PI-функикя; - S-функиия
Інструментарій нечіткої логіки (fuzzy logic toolbox) у складі Matlabнадає можливість формування ФП на основі поліноміальних кривих. Відповідні функції називаються Z-функції (zmf), РІ-функції (pimf) і S-функції (smf). Функція zmfявляє собою асиметричну поліноміальну криву, відкриту ліворуч (мал. П5, , функція smf - дзеркальне відображення функції zmf (мал. П5, ). Відповідно функція pimf дорівнює нулю в правому і лівому межах і приймає значення, що дорівнює одиниці, в середині певного відрізка (мал. П5, в).
Опис функції: = zmf(x, [ab]).
Параметри і bвизначають екстремальні значення кривої (рис. П5, .
Опис функції: = pimf (x, [ab з d]).
Параметри і dзадають перехід функції в нульове значення, а параметри bі с - в одиничний (мал. П5, б).
Опис функції: = smf (х, [а b]) .
Параметри і bвизначають екстремальні значення кривої (рис. П5, в).
Приклад П6. Програма використання поліноміальних кривих
х = 0 : 0,1 : 10;
subplot(1, 3, 1);
= zmf(x, (3 7]);
plot (х, у);
xlabel (" zmf, P= [3 7]");
subplot(1, 3, 2);
= pimf(x, [1 4 5 10]);
plot (x, y);
xlabel ("pimf, P= [1 4 5 10]");
subplot(1, 3, 3);
= smf (x, [1 8]);
plot(x, y);
xlabel ("smf, P=[1 8]").
Крім розглянутих вище функцій, що дозволяють представляти нечіткі безлічі в Mattabє можливість формувати власні ФП або модифікувати вбудовані.