Будь-яка міра інформативності обов'язково базується на понятті ймовірності, що в кожному окремому випадку можна розуміти по-різному. Тому, перш ніж переходити безпосередньо до вивчення кількісних заходів інформації, необхідно розглянути різні концепції ймовірності та проаналізувати їхнім взаємозв'язку.
Поняття ймовірності неоднозначно. До його визначення існує декілька підходів. Практичне значення мають в основному них: частотний, логічний і суб'єктивний.
Найбільш широко поширена концепція об'єктивної ймовірності (частотний підхід). На ній, як правило, розташовуються всі навчальні курси ймовірності та її додатків. Концепція об'єктивної ймовірності застосовна до масових явищ і ґрунтується на припущенні існування об'єктивної характеристики масового явища, яка носить назву ймовірності та наближено вимірюється частотою.
Нехай є нескінченна послідовність результатів випробувань Е1,Е2,..., Еп володіє властивістю иррегулярности, тобто відсутністю закономірності появи результатів даної послідовності. Иррегулярность означає відносну незалежність, відносну автономність елементів послідовності. І нехай подія - деякий безліч із сукупності випробувань, а nA - число появ події п випробуваннях.
Тоді 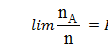 існує і називається ймовірністю події щодо даної сукупності.
існує і називається ймовірністю події щодо даної сукупності.
Таким чином, якщо вважати, як це часто роблять, що концептом об'єктивної ймовірності є єдино можливою, то виявиться, що поняття ймовірності застосовується лише до масових явищ, повторюється багато разів.
Однак концепція об'єктивної ймовірності не є ні єдино можливою, ні навіть в якийсь ступеня привілейованої порівняно з іншими.
В управлінні виробництвом, так і практично в будь-якій галузі діяльності, при прийнятті найбільш важливих, складних рішень доводиться робити висновок від відомого до невідомого. Такий спосіб умовиводи називається індукцією. Якщо визначити невизначеність як незнання достовірного, то можна сказати, що людина постійно має справу з індукцією, долаючи невизначеність. Індукція вивчається індуктивного логікою, яка є одним з розділів формальної логіки. В 17-18 століттях Бекон і Мілль створили так звану класичну індуктивне логіку, яка користувалася природною мовою. У 20 столітті почалася формалізація індуктивного логіки і поняття математичної ймовірності було тим поняттям, що для цього використовували. Індуктивне логіка стала логікою імовірнісної, тобто логікою, що приписує висловлювань не тільки значення істинності або брехні, а й проміжні значення, які вона називає вірогідністю істинності висловлювань.
Позначимо котрусь гіпотезу (вислів) через 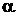 , а дані відомості, на яких ця гіпотеза ґрунтується, через
, а дані відомості, на яких ця гіпотеза ґрунтується, через 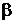 . Зрозуміло, що між висловом
. Зрозуміло, що між висловом 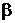 і висловом (гіпотезою)
і висловом (гіпотезою) 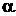 існує певний логічне ставлення. Вислів
існує певний логічне ставлення. Вислів 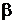 тією чи іншою мірою підтверджує або робить вірогідною гіпотезу
тією чи іншою мірою підтверджує або робить вірогідною гіпотезу 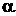 .
.
Міра зв'язку судження і достовірного знання, обумовленості першого другим і називається логічної ймовірністю. 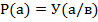
В даний час крім розглянутих двох концепцій знаходить все більше визнання і розвиток, в основному в рампах так званої теорії рішень, концепції суб'єктивної ймовірності. Розглянемо поняття суб'єктивної ймовірності на деякому умовному .примере.
Нехай Е - певна подія і нехай Р - та частина суми S(ставки), яку дачний особа згоден заплатити (S > 0) або отримати (S < 0) за участь у парі, при якому він отримує (платить) S у разі, якщо подія відбувається. Нехай Е1,...,Еп - повна група подій, тобто одне Еiобов'язково відбувається і Еiне настає одночасно, і нехай даними особою призначено відповідні Рi . Якщо Si- сума, яку отримує (платить) особа в разі, коли подія Еi відбудеться, то
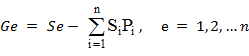
Буде сумарним виграшем (або програшем в залежності від знаку) особи від участі в n парі.
За умови когерентності (несуперечності) призначення, тобто розумності поведінки особи, як неважко показати:
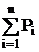 = 1
= 1
Величина Рi - ступінь особистої впевненості даного особу в скоєнні того чи іншого події і є суб'єктивні ймовірності подій.
Слід зауважити, що всі три концепції не тільки не суперечать один одному, але і досить гармонійно поєднуються між собою. Розглянемо це на прикладі.
Припустимо, слід оцінити ймовірність виходу якого-або експерименту. Дати таку оцінку пропонують експертові - людині, що мав справу з подібними експериментами раніше. Його оцінка і буде суб'єктивної ймовірністю цього результату експерименту. Необхідно підкреслити, що об'єктивність даної оцінки полягає лише в тому, що вона несе на собі відображення особистості експерта: неповнота його знань про всіх подібних експериментах і його особистих психічних особливостей. Основа її об'єктивна. Це схожі випадки з практики експерта, тобто цілком достовірна інформація про подібних ситуаціях, що трапилися раніше. Чим більше досвід експерта в даній області, тим менше в його оцінкою суб'єктивного.
Запропонувавши дати подібні оцінки великій групі дуже досвідчених в даному питанні експертів і розрахувавши середню, ми зможемо обчислити вплив індивідуальних особливостей експертів на оцінку і підвищити ступінь її достовірності за рахунок більшої повноти, використання для прогнозу знань схожих результатів експериментів в минулому. Чим більше досвіду, відповідного нагоди ми використовуємо, тим ближче отримана оцінка буде до індуктивного, логічної ймовірності.
Нарешті, повторивши названий експеримент багато разів і розрахувавши частоту виникнення що цікавить нас результату, ми отримаємо оцінку об'єктивної ймовірності його, тим краще, чим більше число раз повторимо експеримент.
Неважко бачити, що в основі всіх трьох ймовірностей результату згаданого експерименту лежать цілком об'єктивні речі. В основі суб'єктивної ймовірності - особистий досвід індивідуума, його знання про результати подібних експериментів в минулому. В основі логічної ймовірності - відомості про всіх схожих експериментах, накопичені цією галуззю знань. В основі об'єктивної (частотної) ймовірності - знання випадків точно таких же експериментів (а не схожих!), що мали місце в минулому.
Таким чином, логічна індуктивна ймовірність є окремим випадком суб'єктивної, коли за рахунок залучення додаткового знання вдається подолати обмеженість особистої індивідуальної оцінки. Об'єктивна ж імовірність є окремим випадком логічної (і, отже, суб'єктивної), коли, багаторазовим повторенням експерименту вдається накопичити достатню інформацію і отримати гарну оцінку ймовірності, що цікавить нас результату. При цьому ясно, що перехід від одного виду ймовірності до іншого здійснюється цілком природно за рахунок накопичення кількості і поліпшення якості інформації.
Важливою особливістю концепцій логічної і суб'єктивної ймовірностей, на відміну від концепції об'єктивної ймовірності є розгляд проблеми ймовірності індивідуального події. Це дозволяє використовувати потужний і добре розроблений апарат математичної теорії ймовірностей для значно більш широкого класу задач управління, ніж це дозволено на базі концепції об'єктивної ймовірності.
Розглянуті концепції по своїй суті є природно-науковими. Вони пояснюють природу, походження, фізичний сенс ймовірності. Поряд з ними існує і математична теорія обчислення ймовірностей, побудована на аксіоматики і не потребує принципі ні в якому природознавчий поясненні. Зазначена теорія є общеприменимым математичним апаратом для всіх трьох концепцій ймовірності.
При розгляді взаємозв'язку трьох концепцій ймовірності впадає в очі, що зв'язок аналогічна зв'язку між собою трьох розділів семіотики: синтактики, семантики і прагматики. Нижче ми переконаємося, що така аналогія не випадкова, а має дуже глибокий теоретичний я практичний сенс.
Виникнення і розвиток основних ідей сучасної синтактики пов'язано з так званою теорії інформації, яку більш правильно слід називати статистичної теорією зв'язку. Теорія зв'язку зародилася разом з телеграфией внаслідок необхідності визначення пропускної здатності і завантаження різних систем зв'язку. Фахівці, які проектували і эксплуатировавшие технічні системи комунікації, цікавилися в першу чергу правильністю передачі сигналів, носіїв повідомлень. Їх не цікавило, та й не могло цікавити зміст повідомлень. У своїй діяльності вони виходили і виходять з того принципу, що якщо телеграф або телефон передають сигналу без спотворення, спілкування буде володіти вигідністю, справжністю, надійністю, новизною і всіма іншими властивостями інформації. Тому й математична теорія зв'язку стосується лише самих сигналів і що міститься в них «кількості інформації», абстрагуючись від всіх специфічних областей її використання людиною.
Будь-який підхід до вимірювання інформації, у тому числі і концепція Шеннона-Вінера, пов'язаний з мірою невизначеності подій, які відбуваються іди будуть відбуватися.
Нехай має місце певна подія , наслідком якого може бути n можливих наслідків (а1, а2,...ап). Припустимо, що якимось чином можна оцінити ймовірність настання кожного результату: Р(а1), Р(а2),...,P(ап). Припустимо, що всі результати рівноймовірні.
Тоді 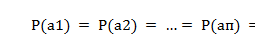
Якщо може мати тільки один вихід (п = 1), то невизначеність події дорівнює нулю. При п = 2 вона буде відмінна від нуля і зі зростанням числа можливих результатів буде збільшуватися.
Розглянемо складне подія АВ, складається з двох незалежних подій і . Подія має п, а подія У - т равновероятных результатів.
Для зручності приймемо, що невизначеність складного події дорівнює сумі невизначеностей складових його простих подій. Проте подія АВ має п'ят равновероятностных результатів. В силу вищесказаного міра невизначеності складного події повинна задовольняти умові:
(пт) = (п) + (т)
Виявляється, що такій умові задовольняє лише логарифмічна функція:
log(nm) = log(n) + log(m)
Тег як результати припущені равновероятными, то очевидно, кожен з них буде вносити в загальну невизначеність події рівну частку, саме 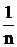 logn. Оскільки
logn. Оскільки 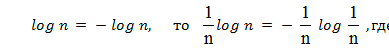 - ймовірність кожного результату. Отже, в загальному випадку невизначеність кожного результату буде визначатися лише логарифмом його ймовірності [- logP(ai)].
- ймовірність кожного результату. Отже, в загальному випадку невизначеність кожного результату буде визначатися лише логарифмом його ймовірності [- logP(ai)].
Так як інформація є міра усунення невизначеності, то її природно вимірювати як різниця невизначеностей певного результату до і після отримання повідомлення. Нехай невизначеність результату до повідомлення здійснення події вимірюється logРо(ai), а після А - logРо(ai). Тоді кількість інформації про кінець ai, отриманої з повідомлення , буде одно I(ai) = logР1(ai) - logРо(ai). Якщо це повідомлення про скоєння результату ai, той Р1(ai) = 1 I I(ai) = - logРо(ai)
З цього з очевидністю випливає, що чий більше вірогідність виходу до здійснення події (апріорна ймовірність); тим менша кількість інформації, що отримується з повідомлення про його здійснення.
Вираз Iaiхарактеризує кількість інформації щодо індивідуального результату ai . Але подія може мати кілька результатів. Ясно, що невизначеність кожного з них пов'язана з невизначеністю події в цілому. Визначимо середню величину невизначеності всіх можливих результатів, зважену з їх ймовірностей
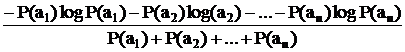 =Н()
=Н()
Н() = 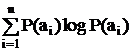
Величина Н(А) називається ентропією події і є мірою його середньої невизначеності. Неважко показати, що вона сягає максимуму при равновероятности всіх випадків і робиться тим менше, чим більше відмінності в можливості, окремих випадків.
Ентропія складного події (АВ) дорівнює сумі энтропий складових його простих подій, але лише за умови, що останні незалежні Н(АВ) = Н(А) + Н(В). Якщо ж і взаємозалежні, то очевидно, що Н(АВ) < Н(А) + Н(В). У разі, коли результат події повністю визначається результатом події , тобто якщо і пов'язані функціональної залежністю Н(АВ) = Н(А). Якщо ж залежність, що зв'язує події і імовірнісна, то Н(АВ) = Н(А) + Н(В/А), (п+1), де Н(В/А) - умовна ентропія події за умови, що подія настав.
Неважко бачити, що міра Шеннона-Вінера є синтактической в самій своїй основі, ймовірно, використовуєте в ній, для вимірювання інформативності повідомлення суть об'єктивні, частотні ймовірності.
Самі творці статистичної теорії зв'язку І. Шеннон і Н. Вінер неодноразово підкреслювали, що негэнтреция, як міра інформативності байдужа до змісту інформації та її одержувачів. Цим багато в чому пояснюється обмежена застосовність заходи Шеннона-Вінера і безплідність численних спроб використовувати її десь поза рамками систем зв'язку.
Тому природно, що робилися численні спроби побудувати інші системи вимірювання інформації, більш придатні для використання в практиці побудови сучасних систем управління виробництвом.
Відомо кілька спроб, що відносяться до можливостей введення кількісної заходи семантичної інформації. Цікавим є те, що всі вони ґрунтувалися на теорії про індуктивного (логічної) ймовірності. Доводиться, що міра семантичної інформації iiповинна бути функцією логічної ймовірності затвердження. Якщо i і j - два вислови і якщо Рі > Pj, то Ii < Ij . При цьому під ймовірністю розуміється не відносна частота, а логічна ймовірність.
Бар-Хіллел і Карнап, найбільш плідно працювали в області побудови теорії семантичної заходи інформації, сформулювали ряд теорем, що стосуються інформаційного змісту висловлювання. Виявилося що їх теорія в багатьох відносинах виявляє аналогію зі статистичної теорією зв'язку Шеннона, проте між ними існують і принципові відмінності.
Теорія Шеннона описує "кількість інформації" об'єктивно, обмежуючись розглядом знаків (сигналів і статистичних відносин між ними. Це синтактическая теорія і як така входить складовою частиною в будь-яку іншу концепції інформації. Розглянуті нею ймовірності являють собою відносні частоти знаків або їх оцінки (об'єктивні ймовірності).
Теорія Бар-Хиллела і Карнапа - семантична, але як така включає також і елементи синтактики. Бар-Хіллел показав, що теорія зв'язку Шеннона може бути повністю відображена в уявленнях семантичної теорії, але не навпаки. Природно, обидві ці теорії не розглядають здійснення конкретних использователей інформації, їх реакцію на ці знаки і т.п., тобто прагматичні аспекти інформації.
досі не з ’ явилося якої єдиної концепції прагматичної заходи інформації. Однак деякі спроби використовувати для вимірювання цінності інформації в рамках байєсівської теорії прийняття рішень виявилися вельми плідними. Загальний підхід до вимірювання цінності інформації зручно розглянути на прикладі, наведеному У. Морісом в книзі «Наука про управлінні. Байєсовський підхід».
Є монета і спеціально виготовлена безкоштовний, чотири сторони якій позначені словом «герб», а інші дві словом «грати». Спостерігати кидання монети і кістки не дозволяється. Один з предметів накривається чашкою.
Нехай
Той - «не накрита монета»;
Т1 - «не накрита кістка»;
- випав «герб»;
- випала «грати».
Якщо приймає рішення вгадає правильно, який саме предмет не накритий, він отримає приз 1 руб. В іншому випадку він не отримує нічого. Ймовірність подій Той і Т1 на початок експерименту вважаються рівними.
(Р) = P(Т1) = 1/2 Очевидно, що в цьому випадку очікуваний виграш Зі = 1/2 руб. Якщо ж точно відомо, яка подія відбудеться, то очікуваний хід (виграш) при наявності повного абсолютної надійної інформації Спп = 1 руб.
Збільшення доходу керівника порівняно з доходом, який він отримав би на основі рішень, прийнятих з допомогою апріорної інформації, будемо називати очікуваної цінністю повної інформації. У нашому прикладі Qnn = Cnn - Co = 1 - 0,5 = 0,5
Отже, максимальна сума, яку має сенс заплатити за абсолютно надійну інформацію в нашому випадку - 0,5 руб. Оскільки Qпп являє собою приріст доходу від повного виключення невизначеності, цю величину іноді називають вартістю невизначеності.
тепер Спробуємо визначити цінність неповної і вибіркової інформації. Для цього розвинемо далі описаний вище приклад з кісткою і монетою.
Особа, що проводить експеримент, повідомляє приймає рішення «гербом» або «ґратами» позначена верхня сторона ненакрытого чашкою предмета. Ясно, що таке повідомлення істотно вплине на думку приймає рішення про те, який предмет накритий чашкою. Інтуїтивно зрозуміло, що при випаданні «те, що не накрита «кістка» - більше певно. Для кількісної оцінки ступеня усунення невизначеності використовується теорія Байєса, яка стверджує, що умовна ймовірність події , якщо відомо, що подія настав, рівного слонової ймовірності події при цьому , помноженої на безумовну ймовірність події та поділений на безумовну ймовірність події .
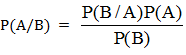
Припустимо, що в нашому експерименті не накрита монета. Тоді умовна ймовірність події а: Р(То) = 1/2, якщо ж не накрита кістка - подія Т, то Р(Т1) = 2/3.
У свою чергу Р(а) = P(Т1)*Р(Т1) + P(То)* (Р) = 7/12
згідно з теоремою Байєса ймовірність того, що накрита кістка, якщо відомо, що випав «герб», визначиться з виразу 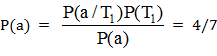 .
.
Аналогічно Р(Те/а) = 3/7. У свою чергу, умовні ймовірності подій Той і Т1 після повідомлення про те, що випала «решітка» - апостериорные ймовірності: Р(Те/в) = 3/5; Р(Т1/в) =2/5. Відповідно, очікуваний дохід при здогадці - «монета» на повідомлення, що випала «решітка» - 3/5 руб., а при здогадці «кістка» - 2/5 руб. Ймовірності повідомлень і рівні 7/12 і 5/12. Очікуваний дохід при даній вибіркової інформації: Свп = 7/12*4/7 + 5/12*3/5 = 7/12 руб. Очікувана цінність вибіркової інформації в нашому випадку: Qвп = 7/12 - 1/2 = 1/12


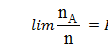 існує і називається ймовірністю події
існує і називається ймовірністю події 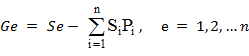
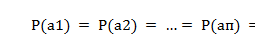
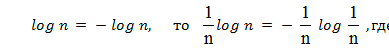 - ймовірність кожного результату. Отже, в загальному випадку невизначеність кожного результату буде визначатися лише логарифмом його ймовірності [- logP(ai)].
- ймовірність кожного результату. Отже, в загальному випадку невизначеність кожного результату буде визначатися лише логарифмом його ймовірності [- logP(ai)].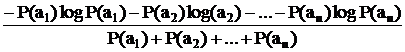 =Н()
=Н()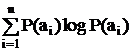
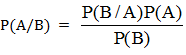
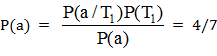 .
.