Відмінності мінімізації систем перемикальних функцій від мінімізації окремих функцій полягають у такому.
Склеювання здійснюються тільки для тих термів, що мають хоча б одну однакову мітку. Отриманому в результаті склеювання терму присвоюється множина міток, що є перетинанням множин міток термів, які склеювались.
Поглинання одного терму іншим здійснюється тільки в тому випадку, коли множини міток двох термів цілком збігаються.
Під час вибору остаточної форми перемикальної функції з використанням таблиці покриттів необхідно прагнути до того, щоб загальне число букв у покритті було мінімальним.
Приклад. Виконати спільну мінімізацію системи перемикальних функцій  , заданих таблицею істинності (табл. 12)
, заданих таблицею істинності (табл. 12)
Таблиця
Параметри функцій
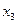  
| 
| 
| 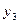
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
|
|
|
|
Для вирішення задачі мінімізації системи перемикальних функцій скористаємося методом Квайна – Мак-Класкі.
Формуємо комплекси кубів 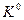 і приписуємо їм відповідні множини міток, що визначають належність термів до певних функцій.
і приписуємо їм відповідні множини міток, що визначають належність термів до певних функцій.
Виконуючи склеювання, послідовно одержимо комплекси кубів 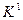 і
і 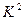 , де множини міток відповідають перетинанням множин міток термів, які склеювались:
, де множини міток відповідають перетинанням множин міток термів, які склеювались:
000 {1, 3} X00 {1}
− − − − − − − −
001 {1, 2. 3} X01 {3}
010 {2} X10 {2}
100 {1, 2} X11 {3} XX1 {3}
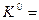 − − − − − − − −
− − − − − − − −  − − − − − − − −
− − − − − − − − 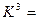
011 {1, 2, 3} 0X1 {1, 2, 3} XX1 {3}
101 {3} 1X0 {1, 2}
110 {1, 2} 1X1 {3}
− − −− − − − − − − − − − − − −
111 {3} 00X {1, 3}
01X {2}
Виконавши поглинання, визначимо імпліканти, що відповідають СДНФ системи:
X00 {1}
X10 {2}
0X1 {1, 2, 3}
Z = 1X0 {1, 2}
00X {1, 3}
01X {2}
XX1 {3}
Складаємо таблицю покриття (табл. ). В заголовках стовпців таблиці покриття записуємо конституенти окремо для кожної функції. Множина міток кожної імпліканти вказує на належність цієї імпліканти до відповідної функції, що необхідно враховувати під час заповнення таблиці.
Таблиця
Таблиця покриття
На підставі таблиці покриття знаходимо остаточні форми зображення функцій:
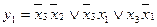 ;
;
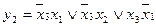 ;
;
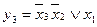 .
.
Одержано загальні імпліканти 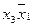 і
і 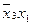 для функцій
для функцій  та
та 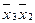 для функцій
для функцій  і
і 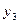 , що забезпечує зменшення складності комбінаційної схеми.
, що забезпечує зменшення складності комбінаційної схеми.
Комбінаційна схема, яка реалізує знайдені форми перемикальних функцій наведена на рис.
Рис. Комбінаційна схема
Під час побудови комбінаційних схем, котрі відповідають системам перемикальних функцій, виникає проблема забезпечення заданого коефіцієнта розгалуження по виходу елементів, що реалізують спільні імпліканти.
Якщо число входів, до яких має бути підключений вихід елемента, перевищує коефіцієнт розгалуження, то застосовують способи дублювання елемента чи посилення сигналу.
У першому випадку в схему вводять необхідну кількість таких самих елементів, входи яких підключено паралельно, а в другому випадку вихідний сигнал підсилюється, наприклад, повторювачем з необхідним коефіцієнтом розгалуження.
На практиці досить часто доводиться реалізовувати сукупності булевих функцій. Якщо здійснити мінімізацію булевих функцій , що входять в систему, незалежно одна від одної, то спільна схема буде складатися із ізольованих під схем. Інколи її можна спростити за рахунок об’єднання ділянок під схем, що реалізують однакові члени, які входять в декілька булевих функцій системи.
Задача мінімізації систем булевих функцій добре досліджена в класі функціонально повних систем: І, АБО, НЕ. Розглянемо один із найпоширеніших методів мінімізації.
Допустимо, задана система повністю визначених булевих функцій, представлених в диз’юнктивній нормальній формі:
 ;
;
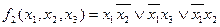 ;
;
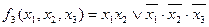 .
.
Всі різні елементарні кон’юнкції системи функцій об’єднаємо в множину  , яку назвемо повною множиною елементарних кон’юнкцій системи функцій. В нашому випадку
, яку назвемо повною множиною елементарних кон’юнкцій системи функцій. В нашому випадку 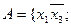


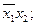
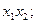
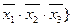 . Сума рангів (число букв) елементарних кон’юнкцій множини
. Сума рангів (число букв) елементарних кон’юнкцій множини  являється зручним критерієм оцінки складності заданої системи булевих функцій.
являється зручним критерієм оцінки складності заданої системи булевих функцій.
Визначення. Система диз’юнктивних нормальних форм булевих функцій називається мінімальною, якщо її повна множина елементарних кон’юнкцій містить мінімальну кількість букв, а кожна диз’юнктивна нормальна форма булевої функції системи містить мінімальне число елементарних кон’юнкцій найменшого рангу. При цьому диз’юнктивна нормальна форма представлення булевої функції в мінімальній системі в загальному випадку не збігається з її мінімальною диз’юнктивною нормальною формою.
Мінімізація систем повністю визначених булевих функцій може здійснюватися за алгоритмом, аналогічним методу Квайна з незначними відмінностями.
Алгоритм мінімізації наступний.
1. Побудувати повну множину  елементарних кон’юнкцій системи функцій, що мінімізується, вважаючи, що спочатку кожна із функцій системи представлена в ДДНФ. Кожній конституенті одиниці множини
елементарних кон’юнкцій системи функцій, що мінімізується, вважаючи, що спочатку кожна із функцій системи представлена в ДДНФ. Кожній конституенті одиниці множини  присвоїти ознаку, яка містить номери функцій системи, в котрі ця конституента входить.
присвоїти ознаку, яка містить номери функцій системи, в котрі ця конституента входить.
2. Виконати мінімізацію ДДНФ функції 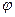 , конституентами одиниці котрої являються всі елементи множини
, конституентами одиниці котрої являються всі елементи множини  . При виконанні склеювань двох конституент одиниці кожній ново утворюваній елементарній кон’юнкції присвоїти ознаку , що складається із номерів функцій , спільних для двох склеюваних конституент одиниці. Останнє справедливе і для двох склеюваних елементарних кон’юнкцій з ознаками. Якщо ознаки склеюваних конституент одиниці не містять спільних номерів, то склеювання не виконується. Поглинання здійснюється тільки для елементарних кон’юнкцій з однаковими ознаками. Одержані в результаті склеювання і поглинання кон’юнкції називаються простими імплікантами системи функцій.
. При виконанні склеювань двох конституент одиниці кожній ново утворюваній елементарній кон’юнкції присвоїти ознаку , що складається із номерів функцій , спільних для двох склеюваних конституент одиниці. Останнє справедливе і для двох склеюваних елементарних кон’юнкцій з ознаками. Якщо ознаки склеюваних конституент одиниці не містять спільних номерів, то склеювання не виконується. Поглинання здійснюється тільки для елементарних кон’юнкцій з однаковими ознаками. Одержані в результаті склеювання і поглинання кон’юнкції називаються простими імплікантами системи функцій.
3. Побудувати імплікантну матрицю функції 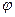 , аналогічну матриці Квайна з тією відмінністю, що для кожної конституенти одиниці відводиться стільки стовпців, скільки різних номерів функцій містить її ознака. Покриття матриці імплікантами виконується аналогічно методу Квайна.
, аналогічну матриці Квайна з тією відмінністю, що для кожної конституенти одиниці відводиться стільки стовпців, скільки різних номерів функцій містить її ознака. Покриття матриці імплікантами виконується аналогічно методу Квайна.
Приклад. Система булевих функцій задана таблицею істиності (табл. 1. 20). Знайти мінімальну ДНФ системи булевих функцій.
Представимо кожну із функцій системи в
Таблиця 1. 20 ДДНФ:
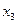  
| 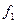 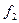
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
| 1 1
0 0
0 1
0 1
0 0
1 1
1 0
1 0
|
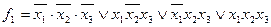 ;
;

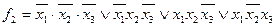 .
.
1. Побудуємо повну множину 
елементарних кон’юнкцій одержаної системи,
приписуючи кожній конституенті одиниці ознаку
входження в функції 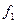 і
і 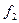 :
:
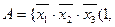
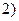 ;
; 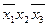
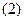 ;
; 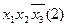 ;
; 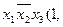
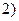 ;
; 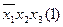 ;
; 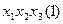 .
.
2. Побудуємо ДДНФ функції 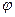 :
:
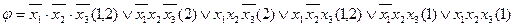 .
.
Для зручності виконання склеювання пронумеруємо кожну конституенту одиниці із ДДНФ функції 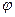 і виконаємо всі склеювання:
і виконаємо всі склеювання:
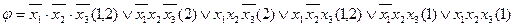 ;
;
1 2 3 4 5 6
1 – 2 : 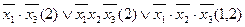 ;
;
2 – 3 :  ;
;
4 – 6 : 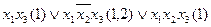 ;
;
5 – 6 : 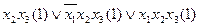 .
.
Після проведення всіх поглинань, з урахуванням ознак кожної кон’юнкції, одержимо
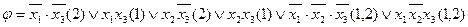 .
.
Подальші склеювання і поглинання неможливі. Одержано прості імпліканти заданої системи булевих функцій.
3. Будуємо імплікантну матрицю (табл. 1. 21). Стовпці матриці позначаємо конституентами одиниці із ДДНФ функції 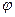 . Для кожної конституенти одиниці відводимо стільки стовпців матриці, скільки різних номерів функцій містить ознака конституенти. Рядки матриці помічаємо простими імплікантами системи булевих функцій. Заповнення матриці виконується аналогічно методу Квайна. Ядром функції
. Для кожної конституенти одиниці відводимо стільки стовпців матриці, скільки різних номерів функцій містить ознака конституенти. Рядки матриці помічаємо простими імплікантами системи булевих функцій. Заповнення матриці виконується аналогічно методу Квайна. Ядром функції 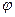 , очевидно, являються прості імпліканти
, очевидно, являються прості імпліканти 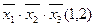 ;
; 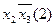 ;
; 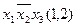 ;
; 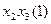 , де для відповідних конституент одиниці функції
, де для відповідних конституент одиниці функції 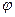 є єдина позначка на перетині стовпця і рядка імплікантної матриці. Вилучене ядро покриває всі
є єдина позначка на перетині стовпця і рядка імплікантної матриці. Вилучене ядро покриває всі
Таблиця 1. 21
| Прості імпліканти системи функцій
| Конституенти одиниці функції 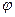
|
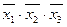
| 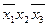 
| 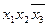
| 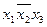
| 
| 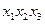
|
|
|
|
|
|
|
|
|
|
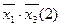
|
| +
| +
|
|
|
|
|
|
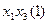
|
|
|
|
| +
|
|
| +
|
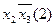
|
|
| +
| +
|
|
|
|
|
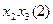
|
|
|
|
|
|
| +
| +
|
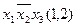
|
|
|
|
| +
| +
|
|
|
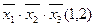
| +
| +
|
|
|
|
|
|
|
конституенти одиниці із ДДНФ функції 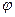 .
.
Відповідно з цим маємо
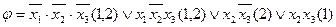 .
.
Вилучивши для функції 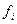 імпліканти з ознакою, що містить
імпліканти з ознакою, що містить 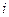 , одержимо наступну мінімальну диз’юнктивну нормальну форму системи функцій:
, одержимо наступну мінімальну диз’юнктивну нормальну форму системи функцій:
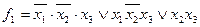 ;
;
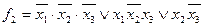 .
.
Велика трудомісткість проведення операцій склеювання і поглинання є недоліком розглянутого методу мінімізації.
1. 6. Методи опису електронних схем
1. 6. 1. Логічні оператори електронних схем
Сукупність логічних елементів , призначена для перетворення двійкових змінних , називається логічною схемою.
Логічний елемент – це електронна схема, що реалізує певну елементарну перемикальну функцію.
Оператором логічного елемента називають функцію, що реалізує цей елемент.
За залежністю вихідного сигналу від вхідного (чи вхідних) сигналу розрізняють:
1. Схеми першого типу – комбінаційні схеми, вихідні сигнали в котрих залежать тільки від стану входів в кожний момент часу.
2. Схеми другого типу – послідовні схеми, що містять схеми накопичення (елементи з пам’яттю). Вихідні сигнали в цих схемах залежить як від вхідних сигналів, так і від стану схеми в попередні моменти часу.
За кількістю входів і виходів розрізняють схеми: з одним входом і одним виходом; з кількома входами і одним виходом; одним входом і кількома виходами; з кількома входами і виходами.
За способом здійснення синхронізації розрізняють: схеми із зовнішньою синхронізацією або синхронні автомати; схеми з внутрішньою синхронізацією (частковий випадок – асинхронні автомати).
Різні як завгодно складні електронні схеми та їх комбінації на логічному рівні можуть бути описані за допомогою логічних операторів. Такий операторний опис електронних схем дозволяє абстрагуватися від фізичної природи конкретних електронних елементів і здійснювати їх аналіз. При цьому для аналізу зовсім не обов’язково мати саму схему , а достатньо мати її логічний оператор. Тоді для аналізу функції на виході будь-якої схеми достатньо записати її у вигляді логічних операторів, зв’язаних між собою у відповідності із виконуваною функцією.
Для аналізу електронної схеми за допомогою апарата алгебри логіки треба знайти логічну функцію, що описує роботу даної схеми. При цьому кожному функціональному елементу схеми ставлять у відповідність логічний оператор.
Декомпозиція перемикальних функцій
За збільшення числа аргументів перемикальної функції процес мінімізації ускладнюється. Методи декомпозиції дозволяють представити функцію як об’єднання кількох функцій, що залежать від меншого числа аргументів. Це спрощує процес мінімізації функції.
Декомпозиція перемикальних функцій методом Шенона дозволяє вилучити будь-яке число змінних, від яких залежить функція. Для виключення однієї змінної використовується таке розкладання:
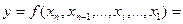
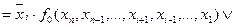 (2. 4)
(2. 4)
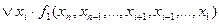 .
.
Функції 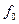 і
і 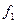 називаються залишковими. Кожна з них залежить від (
називаються залишковими. Кожна з них залежить від ( ) змінних. Схема, що реалізує таке перетворення, зображена на рис. 2. 7. Для залишкових функцій може бути повторно застосоване розкладання (2. 4), що дозволяє виключити наступну змінну. Таким чином, може бути виключене будь-яке число змінних.
) змінних. Схема, що реалізує таке перетворення, зображена на рис. 2. 7. Для залишкових функцій може бути повторно застосоване розкладання (2. 4), що дозволяє виключити наступну змінну. Таким чином, може бути виключене будь-яке число змінних.
Рис. 2. 7. Варіанти реалізації функції
Приклад. Подати функцію 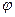 , задану таблицею істинності (табл. ), у вигляді декомпозиції функцій двох змінних.
, задану таблицею істинності (табл. ), у вигляді декомпозиції функцій двох змінних.
Таблиця
Таблиця істинності
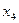 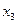  
| 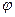
|
|
| 0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
|
|
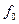
|
| 0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
|
|
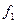
|
| 1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
|
|
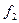
|
| 1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
|
|
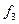
|
Можливі шість варіантів вилучення двох змінних. Нехай вилучаються змінні 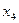 і
і 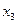 . Тоді отримуємо розклад
. Тоді отримуємо розклад
 .
.
Після мінімізації залишкових функцій одержимо:
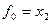 ;
;  ;
; 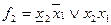 ;
;  .
.
Об’єднання залишкових функцій зручно виконувати за допомогою мультиплексорів.
Розділ 2. АБСТРАКТНІ ЦИФРОВІ АВТОМАТИ
2. 1. Основні поняття
Термін „автомат” використовують двояко. У техніці з поняттям „автомат” пов’язують деякий пристрій, який здатний виконувати визначені функції без втручання людини або за її обмеженою участю. У широкому аспекті, автомат – це математична модель, яка відображає фізичні або абстрактні явища найрізноманітнішої природи. До автоматів можна віднести як реальні пристрої (обчислювальні машини, системи керування і зв’язку, математичні машини, аксіоматичні теорії, лінгвістику та ін.). Отже, комп’ютер живі організми і таке ін.), так і абстрактні системи (м можна розглядати як цифровий (дискретний) автомат, який здійснює приймання, зберігання і перетворення дискретної інформації за заданими алгоритмами.
Загальна теорія автоматів поділяється на абстрактну і структурну.
Абстрактна теорія вивчає поведінку автомата відносно зовнішнього середовища і не розглядає способів його побудови (тобто абстрагуючись від структури автомата). Таким чином, абстрактна теорія автоматів близька до теорії алгоритмів, будучи по суті її подальшою деталізацією.
Структурна теорія автоматів цікавиться як структурою самого автомата, так і структурою вхідних збуджень і реакцією автомата на них. В структурній теорії вивчаються способи побудови автоматів, способи кодування вхідних збуджень і реакції автомата. Отже, структурна теорія автоматів є продовженням і подальшим розвитком абстрактної теорії.
Абстрактний цифровий автомат  визначається сукупністю п’яти об’єктів
визначається сукупністю п’яти об’єктів 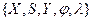 , де
, де 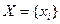 ,
, 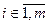 - множина вхідних сигналів автомата
- множина вхідних сигналів автомата  (вхідний алфавіт автомата);
(вхідний алфавіт автомата); 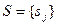 ,
,  - множина станів автомата (алфавіт станів автомата);
- множина станів автомата (алфавіт станів автомата);  ,
, 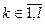 - множина вихідних сигналів автомата
- множина вихідних сигналів автомата  (вихідний алфавіт автомата);
(вихідний алфавіт автомата); 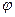 - функція переходів автомата
- функція переходів автомата  , яка задає відображення множин (
, яка задає відображення множин (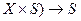 , тобто яка ставить у відповідність будь-якій парі елементів декартового добутку множин (
, тобто яка ставить у відповідність будь-якій парі елементів декартового добутку множин (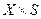 ) елемент
) елемент  ;
; 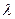 - функція виходів автомата
- функція виходів автомата  , яка задає відображення
, яка задає відображення 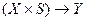 , або
, або 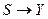 .
.
За способом формування функції виходів розрізняють три типи абстрактних автоматів: автомат Мілі, автомат Мура і С-автомати. В автоматі Мілі функція виходів 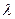 задає відображення
задає відображення 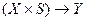 . В автоматі Мура функція виходів
. В автоматі Мура функція виходів 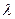 задає відображення
задає відображення 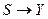 . В абстрактному С-автоматі вводяться дві функції виходів
. В абстрактному С-автоматі вводяться дві функції виходів 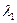 і
і 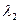 , які задають відображення
, які задають відображення 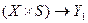 і
і 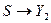 відповідно. При цьому алфавіт виходів С-автомата
відповідно. При цьому алфавіт виходів С-автомата 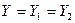 або
або 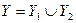 .
.
Довільний абстрактний автомат Мілі чи Мура має один вхідний і один вихідний канали (рис. 2. 1,а). Довільний абстрактний С-автомат має один вхідний і два вихідних канали (рис. 2. 1,б).
Рис. 2. 1. Структура абстрактних автоматів: а – Мілі та Мура;
б – С-автомата.
Розрізняють повністю визначені і часткові автомати.
Повністю визначеним називається абстрактний цифровий автомат, у якого функція переходів і функція виходів визначені для всіх пар (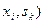 .
.
Частковим називається цифровий абстрактний автомат, у якого функція переходів чи функція виходів, або обидві ці функції визначені не для всіх пар (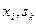 ).
).
Абстрактний цифровий автомат називається ініціальним, якщо на множині його станів  вилучається спеціальний початковий стан
вилучається спеціальний початковий стан 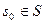 , тобто ініціальний абстрактний автомат визначається сукупністю шести об’єктів
, тобто ініціальний абстрактний автомат визначається сукупністю шести об’єктів 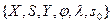 .Вилучення на множині
.Вилучення на множині  початкового стану
початкового стану 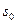 пояснюється чисто практичними міркуваннями, пов’язаними із виникаючою часто необхідністю фіксувати умови початку роботи автомата.
пояснюється чисто практичними міркуваннями, пов’язаними із виникаючою часто необхідністю фіксувати умови початку роботи автомата.
Автомат працює в дискретному автоматному часі 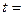 0, 1, 2, ... і переходи із стану в стан здійснюються миттєво. В кожний момент
0, 1, 2, ... і переходи із стану в стан здійснюються миттєво. В кожний момент 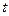 дискретного часу автомат знаходиться в деякому стані
дискретного часу автомат знаходиться в деякому стані 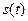 із множини станів
із множини станів  . Якщо автоматі ініціальний , то в початковий момент часу
. Якщо автоматі ініціальний , то в початковий момент часу 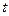 = 0 він завжди знаходиться в початковому стані
= 0 він завжди знаходиться в початковому стані 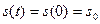 . В момент
. В момент 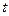 , знаходячись в стані
, знаходячись в стані 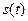 , автомат здатен сприйняти на вході букву вхідного алфавіту
, автомат здатен сприйняти на вході букву вхідного алфавіту 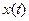
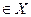 . У відповідності із функцією виходів
. У відповідності із функцією виходів 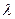 він видасть у той же момент часу
він видасть у той же момент часу 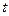 букву вихідного алфавіту
букву вихідного алфавіту 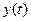 і у відповідності із функцією переходів
і у відповідності із функцією переходів 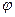 перейде в наступний стан
перейде в наступний стан 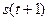 . Згідно із визначенням абстрактного автомата, автомат Мілі в цьому разі характеризується системою рівнянь:
. Згідно із визначенням абстрактного автомата, автомат Мілі в цьому разі характеризується системою рівнянь:
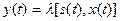 ,
,
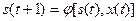 ;
;
автомат Мура – системою рівнянь:
 ,
,
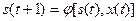 ,
,
а С-автомат – системою рівнянь:
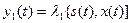 ,
,
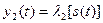 ,
,
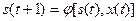 .
.
Іншими словами, якщо на вхід ініціального автомата Мілі чи Мура, який установлений у початковий стан 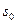 , подавати буква за буквою деяку послідовність букв вхідного алфавіту
, подавати буква за буквою деяку послідовність букв вхідного алфавіту 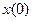 ,
, 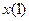 ,
, 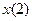 , ...- вхідне слово, то на виході автомата будуть появлятися букви вихідного алфавіту
, ...- вхідне слово, то на виході автомата будуть появлятися букви вихідного алфавіту 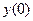 ,
,  ,
, 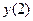 , ... - вихідне слово. Для випадку С-автомата на його виходах будуть появлятися дві послідовності:
, ... - вихідне слово. Для випадку С-автомата на його виходах будуть появлятися дві послідовності: 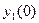 ,
, 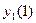 ,
, 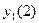 , ... і
, ... і 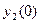 ,
,  ,
, 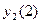 ,...
,...
Таким чином, на рівні абстрактної теорії функціонування цифрового автомата розуміється як перетворення вхідних слів у вихідні слова.
Поняття стану у визначенні абстрактного автомата введено у зв’язку з тим, що вихідний сигнал, що видається автоматом в даний момент часу , залежить як від вхідних сигналів в даний момент часу, так і від стану, в якому автомат в даний момент знаходився.
Ряд процесів, якими керують реальні автомати , не вимагають для своєї роботи знання попередньої історії. В них вихідний сигнал визначається тільки вхідними сигналами. Такі автомати мають тільки один стан. Їх задають трійкою 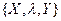 , де функція виходів
, де функція виходів 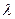 - це відображення (
- це відображення (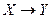 ), тобто
), тобто 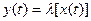 . Автомати з одним внутрішнім станом називаються абстрактними автоматами з тривіальною пам’яттю (без пам’яті) або комбінаційними автоматами.
. Автомати з одним внутрішнім станом називаються абстрактними автоматами з тривіальною пам’яттю (без пам’яті) або комбінаційними автоматами.
Алфавіти входів, станів і виходів автоматів задаються, як звичайні множини, наприклад, переліком своїх елементів. Функції переходів і виходів можуть бути задані матрично, графічно і аналітично. Тому будь-який абстрактний автомат може бути заданий трьома способами: матрично, графічно і аналітично.
При матричному способі автомат представляються або двома таблицями: таблицею переходів і таблицею виходів, або матрицею з’єднань. Таблиця переходів задає відображення (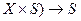 , тобто визначає функцію переходів автомата. Таблиця виходів, в залежності від типу розглядуваного автомата, задає або відображення
, тобто визначає функцію переходів автомата. Таблиця виходів, в залежності від типу розглядуваного автомата, задає або відображення 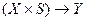 , або
, або 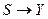 , тобто визначає функцію виходів автомата.
, тобто визначає функцію виходів автомата.
Таблиця переходів довільного повністю визначеного абстрактного автомата будується так. Стовпці таблиці позначаються буквами вхідного алфавіту автомата, а рядки таблиці – буквами алфавіту станів автомата. В клітинці таблиці переходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом 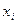 , і рядка, позначеного станом
, і рядка, позначеного станом 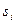 , ставиться стан
, ставиться стан 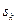 , що є результатом переходу автомата із стану
, що є результатом переходу автомата із стану 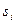 під дією вхідного сигналу
під дією вхідного сигналу 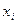 , що визначається виразом
, що визначається виразом 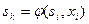 . Приклад таблиці переходів деякого абстрактного повного автомата із вхідним алфавітом
. Приклад таблиці переходів деякого абстрактного повного автомата із вхідним алфавітом 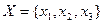 і алфавітом станів
і алфавітом станів  представлений у табл. 2. 1. Якщо абстрактний автомат частковий, то в клітині таблиці його переходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом
представлений у табл. 2. 1. Якщо абстрактний автомат частковий, то в клітині таблиці його переходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом  , і рядка, позначеного станом
, і рядка, позначеного станом 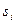 (при умові, що перехід із стану
(при умові, що перехід із стану 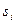 під дією вхідного сигналу
під дією вхідного сигналу  невизначений), ставиться прочерк, і будь-яке вхідне слово, яке приводить до вказаного переходу, є забороненим. Інші клітинки заповнюються так само, як і для повного автомата. Приклад таблиці переходів деякого абстрактного часткового автомата з вхідним алфавітом
невизначений), ставиться прочерк, і будь-яке вхідне слово, яке приводить до вказаного переходу, є забороненим. Інші клітинки заповнюються так само, як і для повного автомата. Приклад таблиці переходів деякого абстрактного часткового автомата з вхідним алфавітом
Таблиця 2. 1 Таблиця 2. 2
| Стани
| Вхідні сигнали
|
| Стани
| Вхідні сигнали
|
|

| 
| 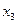
| 
| 
|


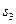
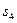
| 
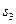
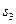
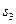
| 
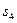


| 

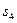
 
| 

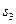
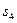
|  -
-
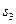 -
-
| -
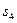


|
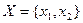 і алфавітом станів
і алфавітом станів  представлений в табл. 2. 2. Вигляд таблиці переходів не залежить від типу автомата, що задається (автомат Мура, Мілі чи С-автомат). Таблиці виходів автомата Мура, Мілі, С-автомата мають відмінності.
представлений в табл. 2. 2. Вигляд таблиці переходів не залежить від типу автомата, що задається (автомат Мура, Мілі чи С-автомат). Таблиці виходів автомата Мура, Мілі, С-автомата мають відмінності.
Таблиця виходів повного автомата Мілі будується так. В клітинці таблиці виходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом  , і рядка, позначеного станом
, і рядка, позначеного станом 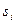 , ставиться вихідний сигнал
, ставиться вихідний сигнал 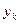 , котрий автомат Мілі видає, перебуваючи в стані
, котрий автомат Мілі видає, перебуваючи в стані 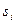 під дією вхідного сигналу
під дією вхідного сигналу  , що визначається виразом
, що визначається виразом 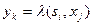 . Приклад таблиці виходів деякого абстрактного повного автомата Мілі із вхідним алфавітом
. Приклад таблиці виходів деякого абстрактного повного автомата Мілі із вхідним алфавітом 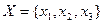 , алфавітом станів
, алфавітом станів  і вихідним алфавітом
і вихідним алфавітом 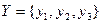 представлений в табл. 2. 3.
представлений в табл. 2. 3.
Таблиця виходів повного автомата Мура будується простіше: кожному стану автомата приписується свій вихідний сигнал. Приклад таблиці виходів автомата Мура з алфавітом станів  і вихідним алфавітом
і вихідним алфавітом
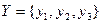 представлений у табл. 2. 4.
представлений у табл. 2. 4.
Таблиця 2. 3 Таблиця 2. 4
| Стани
| Вхідні сигнали
|
| Стани
| Вихідні
сигнали
|

| 
| 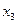
|


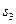
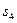
| 
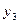 


| 
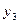


| 
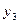
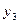
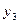
| 

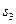
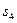
| 


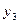
|
Абстрактний повний С-автомат задається двома таблицями виходів, перша з яких є таблиця виходів Мілі, а друга – таблиця виходів автомата Мура.
Якщо автомат Мілі частковий, то в деяких клітинках його таблиці виходів може стояти прочерк, який означає відсутність вихідного сигналу. При цьому прочерк обов’язково ставиться в тих клітинках таблиці виходів, котрі відповідають таким же клітинкам з прочерком в таблиці переходів автомата Мілі. Приклад таблиці виходів часткового автомата Мілі, заданого таблицею переходів (табл. 2. 2) із вхідним алфавітом 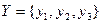 , представлений в табл. 2. 5.
, представлений в табл. 2. 5.
Прочерки в деяких клітинках таблиці виходів часткового автомата Мура не зв’язані з прочерками у клітинках його таблиці переходів. Це визначається тим, що вихідний сигнал автомата Мура залежить тільки від стану, в якому знаходиться автомат. Наприклад, таблиця виходів часткового автомата Мура, заданого таблицею переходів (табл. 2. 2), може бути представлена і як табл. 2. 4, якщо в кожному своєму стані автомат видає який-небудь вихідний сигнал, і як табл. 2. 6, якщо значення вихідного сигналу автомата для деяких станів невизначене.
Таблиця 2. 5 Таблиця 2. 6
| Стани
| Вхідні сигнали
|
| Стани
| Вихідні
сигнали
|

| 
|


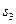
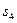
|  -
-
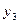 -
-
| -
 -
-
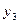
| 

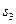
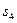
|  -
-

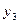
|
На практиці таблиці переходів і виходів автомата часто суміщають у одну таблицю, що називається позначеною таблицею переходів автомата. Така таблиця переходів повного автомата Мілі, який представлений таблицею переходів (табл. 2. 1) і таблицею виходів (табл. 2. 3), зведена в табл. 2. 7. Позначена таблиця переходів часткового автомата Мура (табл. 2. 2) і таблиця виходів (табл. 2. 4) зведена в табл. 2. 8.
Крім таблиць переходів і виходів довільний абстрактний автомат може бути описаний матрицею з’єднань. Такий опис є одним із способів матричного завдання абстрактних автоматів. Матриця з’єднань довільного абстрактного автомата являється квадратною і містить стільки стовпців (рядків), скільки різних станів має даний автомат. Кожний стовпець (рядок0 матриці з’єднань позначається буквою станів автомата. Якщо автомат ініціальний, то перший зліва стовпець і перший зверху рядок матриці його з’єднань позначаються буквою початкового стану автомата. В клітинці матриці з’єднань, яка знаходиться на перетині стовпця, позначеного буквою стану  і рядка. Позначеного буквою стану
і рядка. Позначеного буквою стану 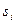 автомата, ставиться вхідний сигнал
автомата, ставиться вхідний сигнал 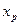 (або диз’юнкція вхідних сигналів), під дією котрих виконується перехід автомата із стану
(або диз’юнкція вхідних сигналів), під дією котрих виконується перехід автомата із стану  в стан
в стан 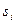 . Якщо матрицею з’єднань задається
. Якщо матрицею з’єднань задається
Таблиця 2. 7 Таблиця 2. 8
| Стан
| Вхідні сигнали
|
| Стани
| Вхідні сигнали
| Вихідні
сигнали
|

| 
| 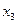
|
|
|

| 

| 

| 

|  
| 
| -
| 
|

| 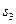 
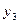
| 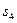
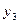
| 

| 
|  - -
| 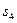
| 
|
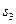
| 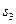

| 

| 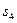
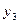
| 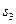
| 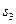
| 
| 
|
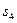
| 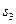

| 

| 
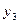
| 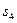
| -
| 
| 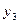
|
абстрактний автомат Мілі, то поряд із буквою вхідного сигналу 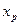 в дужках вказується буква вихідного сигналу
в дужках вказується буква вихідного сигналу 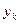 , який видає автомат Мілі, здійснюючи перехід
, який видає автомат Мілі, здійснюючи перехід 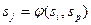 . Матриця з’єднань деякого автомата Мілі, представленого позначеною таблицею переходів (табл. 2. 7), показана на рис. 2. 2.
. Матриця з’єднань деякого автомата Мілі, представленого позначеною таблицею переходів (табл. 2. 7), показана на рис. 2. 2.


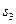
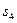




Рис.2. 2. Матриця з’єднань автомата Мілі.
Якщо матрицею з’єднань задається абстрактний автомат Мура, то вихідними сигналами позначаються стани автомата, які ідентифікують рядки матриці з’єднань.
При графічному способі задавання абстрактні автомати представляються орієнтованими графами. Стани автомата зображаються вершинами графа, а переходи між станами – дугами між відповідними вершинами. При цьому кожній дузі графа приписується деяка буква 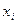 вхідного алфавіту автомата, яка вказує, що даний перехід автомата виконується тільки при появі вхідного сигналу
вхідного алфавіту автомата, яка вказує, що даний перехід автомата виконується тільки при появі вхідного сигналу 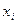 , а кожній вершині графа – буква відповідного стану автомата. Якщо графом зображається автомат Мілі, то вихідні сигнали автомата проставляються на дугах графа (у відповідності з таблицею виходів автомата) поряд із буквою вхідного сигналу. Приклад графа автомата Мілі, заданого таблицею переходів (табл. 2. 1) і таблицею виходів (табл. 2. 3), показаний на рис. 2. 3, а. Якщо графом зображається автомат Мура, то вихідні сигнали автомата проставляються біля вершин графа (у відповідності із таблицею виходів автомата). Приклад графа автомата Мура, заданого таблицею переходів (табл. 2. 2) і таблицею виходів (табл. 2. 4), показаний на рис.2. 3,б.
, а кожній вершині графа – буква відповідного стану автомата. Якщо графом зображається автомат Мілі, то вихідні сигнали автомата проставляються на дугах графа (у відповідності з таблицею виходів автомата) поряд із буквою вхідного сигналу. Приклад графа автомата Мілі, заданого таблицею переходів (табл. 2. 1) і таблицею виходів (табл. 2. 3), показаний на рис. 2. 3, а. Якщо графом зображається автомат Мура, то вихідні сигнали автомата проставляються біля вершин графа (у відповідності із таблицею виходів автомата). Приклад графа автомата Мура, заданого таблицею переходів (табл. 2. 2) і таблицею виходів (табл. 2. 4), показаний на рис.2. 3,б.
Рис. 2. 3. Граф: а – автомата Мілі; б – автомата Мура.
При аналітичному способі задавання абстрактні автомати представляються четвіркою об’єктів 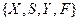 , де
, де 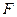 задає для кожного стану
задає для кожного стану 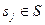 автомата відображення (
автомата відображення (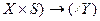 . Іншими словами, при аналітичному способі задавання для кожного стану
. Іншими словами, при аналітичному способі задавання для кожного стану 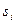 автомата вказується відображення
автомата вказується відображення 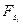 , яке становить собою множину всіх трійок
, яке становить собою множину всіх трійок 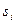 ,
, 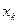 .
. 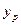 , і таких, що під дією вхідного сигналу
, і таких, що під дією вхідного сигналу 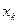 автомат виконує перехід із стану
автомат виконує перехід із стану 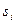 в стан
в стан  , видаючи при цьому вихідний сигнал
, видаючи при цьому вихідний сигнал 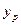 . Відображення
. Відображення 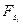 записується так:
записується так: 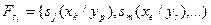 .
.
Аналітичне задавання автомата Мілі, представленого позначеною таблицею переходів (табл. 2. 7, має такий вигляд
Автомат 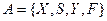 ,
, 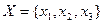 ,
,  ,
, 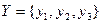 ,
,
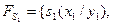

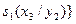 ;
;
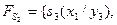
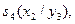
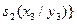 ;
;
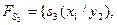

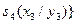 ;
;
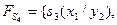

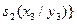 .
.
Розглянемо еквівалентне перетворення автоматів. Еквівалентними називаються автомати, що індукують одне й те ж відображення множини слів у вхідному алфавіті у множину слів у вихідному алфавіті. Розглянемо тільки перетворення автомата Мура в еквівалентний йому автомат Мілі. Перетворення автомата Мілі в еквівалентний йому автомат Мура здійснюється дещо складніше.
Перехід від автомата Мура до еквівалентного йому автомата Мілі зручно здійснювати при графічному способі завдання автоматів. В цьому разі ві зводиться до перенесення вихідного сигналу 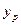 , що видається автоматом Мура в стані
, що видається автоматом Мура в стані  на дуги, що входять в вершину, позначену буквою
на дуги, що входять в вершину, позначену буквою  . При матричному способі завдання таблиця переходів автомата Мілі збігається з таблицею переходів автомата Мура, а таблиця виходів автомата Мілі виходить із його таблиці переходів заміною букви стану
. При матричному способі завдання таблиця переходів автомата Мілі збігається з таблицею переходів автомата Мура, а таблиця виходів автомата Мілі виходить із його таблиці переходів заміною букви стану  , яка знаходиться на перетині стовпця, позначеного вхідним сигналом
, яка знаходиться на перетині стовпця, позначеного вхідним сигналом 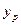 , що видається автоматом Мура в стані
, що видається автоматом Мура в стані  .
.
Розробка реальних автоматів (представлених хоча б на рівні принципових електричних схем) вимагає їх завдання спочатку на абстрактному рівні з наступним переходом на структурний рівень, який враховує використовувані в схемі автомата логічні елементи і зв’язки між ними. В зв’язку з цим виникає задача синтезу абстрактного автомата, виходячи із деякого початкового, наприклад, словесного описання його роботи.
На завершення відзначимо, що ми розглядаємо тільки детерміновані автомати, у яких виконана умова однозначності переходів: автомат, який знаходиться в деякому стані, під дією будь-якого вхідного сигналу не може перейти більше ніж в один стан. Автомат, заданий таблицею переходів, завжди детермінований, оскільки на перетині стовпця  і рядка
і рядка 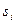 таблиці переходів записується тільки один стан
таблиці переходів записується тільки один стан  , якщо перехід визначений, і ставиться прочерк, якщо перехід не визначений. Стосовно графічного способу завдання автомата умова однозначності означає, що в графі автомата із будь-якої вершини не може виходити дві і більше дуги, позначені одним і тим же вхідним сигналом.
, якщо перехід визначений, і ставиться прочерк, якщо перехід не визначений. Стосовно графічного способу завдання автомата умова однозначності означає, що в графі автомата із будь-якої вершини не може виходити дві і більше дуги, позначені одним і тим же вхідним сигналом.
Розділ 3.СИНТЕЗ КОМБІНАЦІЙНИХ СХЕМ
Синтез комбінаційних схем на логічних елементах
Задача синтезу полягає у проектуванні при заданих вхідних змінних і відомій вихідній функції логічного пристрою, що реалізує цю функцію.
Система функцій, яка реалізується вибраною для синтезу схем сукупністю логічних елементів, завжди має бути функціонально повною, тобто такою, що допускає реалізацію будь-якої функції на основі принципу суперпозиції. Мінімізацію функцій можна виконувати у різних алгебрах. У зв’язку з цим відомі різні методи побудови комбінаційних схем. Розглянемо один із можливих підходів до побудови комбінаційних схем у елементному базисі трьох алгебр: Буля, Шефера і Пірса.
Синтез комбінаційних схем у заданому елементному базисі можна розділити на три етапи.
На першому етапі виконують мінімізацію перемикальних функцій обраним методом.
На другому етапі функції подають у можливих операторних формах, тобто у вигляді суперпозиції операторів заданих логічних елементів.
На третьому етапі з урахуванням цільової функції проектування обирають операторну форму перемикальної функ


 , заданих таблицею істинності (табл. 12)
, заданих таблицею істинності (табл. 12)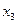




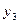
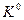 і приписуємо їм відповідні множини міток, що визначають належність термів до певних функцій.
і приписуємо їм відповідні множини міток, що визначають належність термів до певних функцій.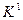 і
і 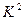 , де множини міток відповідають перетинанням множин міток термів, які склеювались:
, де множини міток відповідають перетинанням множин міток термів, які склеювались: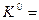 − − − − − − − −
− − − − − − − −  − − − − − − − −
− − − − − − − − 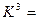
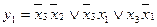 ;
;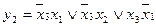 ;
;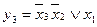 .
.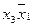 і
і 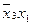 для функцій
для функцій  та
та 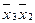 для функцій
для функцій  ;
;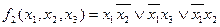 ;
;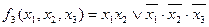 .
. , яку назвемо повною множиною елементарних кон’юнкцій системи функцій. В нашому випадку
, яку назвемо повною множиною елементарних кон’юнкцій системи функцій. В нашому випадку 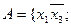


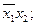
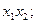
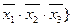 . Сума рангів (число букв) елементарних кон’юнкцій множини
. Сума рангів (число букв) елементарних кон’юнкцій множини 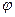 , конституентами одиниці котрої являються всі елементи множини
, конституентами одиниці котрої являються всі елементи множини 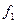
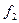
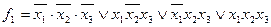 ;
;
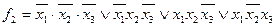 .
.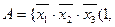
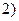 ;
; 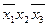
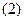 ;
; 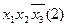 ;
; 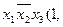
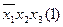 ;
; 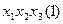 .
.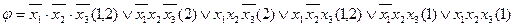 .
.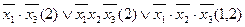 ;
; ;
;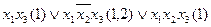 ;
;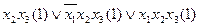 .
.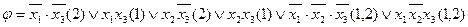 .
.
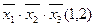 ;
; 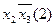 ;
; 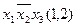 ;
; 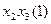 , де для відповідних конституент одиниці функції
, де для відповідних конституент одиниці функції 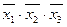
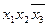
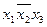

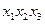
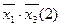
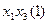
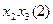
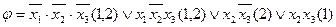 .
.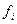 імпліканти з ознакою, що містить
імпліканти з ознакою, що містить 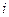 , одержимо наступну мінімальну диз’юнктивну нормальну форму системи функцій:
, одержимо наступну мінімальну диз’юнктивну нормальну форму системи функцій: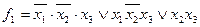 ;
;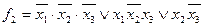 .
.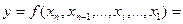
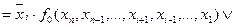 (2. 4)
(2. 4)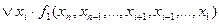 .
.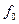 і
і  ) змінних. Схема, що реалізує таке перетворення, зображена на рис. 2. 7. Для залишкових функцій може бути повторно застосоване розкладання (2. 4), що дозволяє виключити наступну змінну. Таким чином, може бути виключене будь-яке число змінних.
) змінних. Схема, що реалізує таке перетворення, зображена на рис. 2. 7. Для залишкових функцій може бути повторно застосоване розкладання (2. 4), що дозволяє виключити наступну змінну. Таким чином, може бути виключене будь-яке число змінних.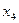
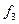
 .
.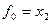 ;
;  ;
; 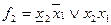 ;
;  .
.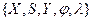 , де
, де 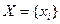 ,
, 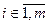 - множина вхідних сигналів автомата
- множина вхідних сигналів автомата 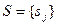 ,
,  - множина станів автомата (алфавіт станів автомата);
- множина станів автомата (алфавіт станів автомата);  ,
, 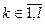 - множина вихідних сигналів автомата
- множина вихідних сигналів автомата 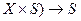 , тобто яка ставить у відповідність будь-якій парі елементів декартового добутку множин (
, тобто яка ставить у відповідність будь-якій парі елементів декартового добутку множин (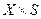 ) елемент
) елемент  ;
; 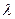 - функція виходів автомата
- функція виходів автомата 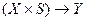 , або
, або 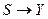 .
.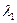 і
і 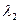 , які задають відображення
, які задають відображення 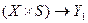 і
і 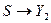 відповідно. При цьому алфавіт виходів С-автомата
відповідно. При цьому алфавіт виходів С-автомата 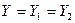 або
або 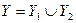 .
.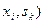 .
.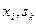 ).
).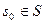 , тобто ініціальний абстрактний автомат визначається сукупністю шести об’єктів
, тобто ініціальний абстрактний автомат визначається сукупністю шести об’єктів 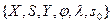 .Вилучення на множині
.Вилучення на множині 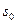 пояснюється чисто практичними міркуваннями, пов’язаними із виникаючою часто необхідністю фіксувати умови початку роботи автомата.
пояснюється чисто практичними міркуваннями, пов’язаними із виникаючою часто необхідністю фіксувати умови початку роботи автомата.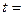 0, 1, 2, ... і переходи із стану в стан здійснюються миттєво. В кожний момент
0, 1, 2, ... і переходи із стану в стан здійснюються миттєво. В кожний момент 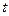 дискретного часу автомат знаходиться в деякому стані
дискретного часу автомат знаходиться в деякому стані 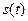 із множини станів
із множини станів 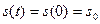 . В момент
. В момент 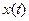
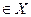 . У відповідності із функцією виходів
. У відповідності із функцією виходів 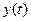 і у відповідності із функцією переходів
і у відповідності із функцією переходів 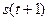 . Згідно із визначенням абстрактного автомата, автомат Мілі в цьому разі характеризується системою рівнянь:
. Згідно із визначенням абстрактного автомата, автомат Мілі в цьому разі характеризується системою рівнянь: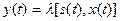 ,
,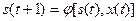 ;
; ,
,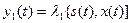 ,
,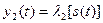 ,
,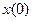 ,
, 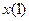 ,
, 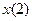 , ...- вхідне слово, то на виході автомата будуть появлятися букви вихідного алфавіту
, ...- вхідне слово, то на виході автомата будуть появлятися букви вихідного алфавіту 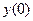 ,
,  ,
, 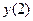 , ... - вихідне слово. Для випадку С-автомата на його виходах будуть появлятися дві послідовності:
, ... - вихідне слово. Для випадку С-автомата на його виходах будуть появлятися дві послідовності: 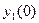 ,
, 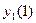 ,
, 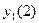 , ... і
, ... і 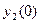 ,
,  ,
, 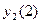 ,...
,...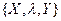 , де функція виходів
, де функція виходів 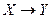 ), тобто
), тобто 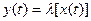 . Автомати з одним внутрішнім станом називаються абстрактними автоматами з тривіальною пам’яттю (без пам’яті) або комбінаційними автоматами.
. Автомати з одним внутрішнім станом називаються абстрактними автоматами з тривіальною пам’яттю (без пам’яті) або комбінаційними автоматами.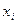 , і рядка, позначеного станом
, і рядка, позначеного станом 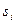 , ставиться стан
, ставиться стан 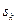 , що є результатом переходу автомата із стану
, що є результатом переходу автомата із стану 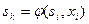 . Приклад таблиці переходів деякого абстрактного повного автомата із вхідним алфавітом
. Приклад таблиці переходів деякого абстрактного повного автомата із вхідним алфавітом 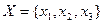 і алфавітом станів
і алфавітом станів  представлений у табл. 2. 1. Якщо абстрактний автомат частковий, то в клітині таблиці його переходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом
представлений у табл. 2. 1. Якщо абстрактний автомат частковий, то в клітині таблиці його переходів, яка знаходиться на перетині стовпця, позначеного вхідним сигналом  , і рядка, позначеного станом
, і рядка, позначеного станом 

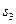
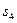
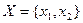 і алфавітом станів
і алфавітом станів 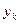 , котрий автомат Мілі видає, перебуваючи в стані
, котрий автомат Мілі видає, перебуваючи в стані 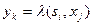 . Приклад таблиці виходів деякого абстрактного повного автомата Мілі із вхідним алфавітом
. Приклад таблиці виходів деякого абстрактного повного автомата Мілі із вхідним алфавітом 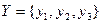 представлений в табл. 2. 3.
представлений в табл. 2. 3. і рядка. Позначеного буквою стану
і рядка. Позначеного буквою стану 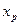 (або диз’юнкція вхідних сигналів), під дією котрих виконується перехід автомата із стану
(або диз’юнкція вхідних сигналів), під дією котрих виконується перехід автомата із стану 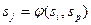 . Матриця з’єднань деякого автомата Мілі, представленого позначеною таблицею переходів (табл. 2. 7), показана на рис. 2. 2.
. Матриця з’єднань деякого автомата Мілі, представленого позначеною таблицею переходів (табл. 2. 7), показана на рис. 2. 2.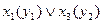
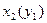
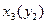
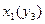
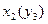
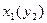


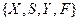 , де
, де 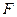 задає для кожного стану
задає для кожного стану 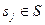 автомата відображення (
автомата відображення (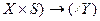 . Іншими словами, при аналітичному способі задавання для кожного стану
. Іншими словами, при аналітичному способі задавання для кожного стану 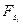 , яке становить собою множину всіх трійок
, яке становить собою множину всіх трійок 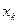 .
. 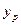 , і таких, що під дією вхідного сигналу
, і таких, що під дією вхідного сигналу 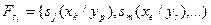 .
.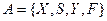 ,
, 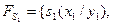

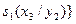 ;
;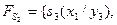
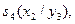
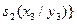 ;
;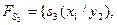

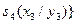 ;
;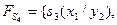
 , якщо перехід визначений, і ставиться прочерк, якщо перехід не визначений. Стосовно графічного способу завдання автомата умова однозначності означає, що в графі автомата із будь-якої вершини не може виходити дві і більше дуги, позначені одним і тим же вхідним сигналом.
, якщо перехід визначений, і ставиться прочерк, якщо перехід не визначений. Стосовно графічного способу завдання автомата умова однозначності означає, що в графі автомата із будь-якої вершини не може виходити дві і більше дуги, позначені одним і тим же вхідним сигналом.