2. Замінити знак операції АБО між термами на ВИКЛЮЧНЕ АБО ( ). Наприклад, якщо ДДНФ перемикальної функції має вигляд
). Наприклад, якщо ДДНФ перемикальної функції має вигляд
 ,
,
то, замінивши знак операції АБО між термами на ВИКЛЮЧНЕ АБО, можна записати
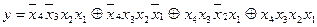 .
.
Така заміна правомірна, якщо функція представлена в ДДНФ. Це пояснюється тим, що ДДНФ складається тільки із конституент одиниці, Отже, на будь-якому наборі аргументів тільки одна конституента приймає одиничне значення, а всі інші – нульові. Таким чином, виконується рівність такого вигляду:
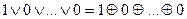 ,
,
де положення одиниці у запису може бути довільним.
3. Кожний аргумент із запереченням замінити на суму за модулем два цього аргументу з одиницею згідно з аксіомою 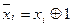 .
.
4. Розкрити дужки й спростити одержаний вираз шляхом викреслювання парних термів згідно з аксіомами 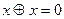 ;
; 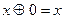 .
.
Виконавши послідовно етапи 3 та 4, одержимо канонічну нормальну форму в алгебрі Жегалкіна заданої перемикальної функції:


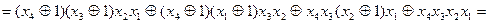

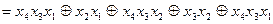 .
.
Приклад. Одержати канонічні нормальні форми в алгебрі Жегалкіна функцій  і
і  , заданих таблицею істинності (табл. 1. 9).
, заданих таблицею істинності (табл. 1. 9).
Таблиця 1. 9
 
|  
|
| 0 0
0 1
1 0
1 1
| 0 0
1 1
1 1
1 0
|
Функції  і
і  є відповідно функціями І та ВИКЛЮЧНЕ АБО, що очевидно із табл. 1. 9. Представимо задані функції у ДДНФ і виконаємо послідовно етапи перетворення форм перемикальних функцій.
є відповідно функціями І та ВИКЛЮЧНЕ АБО, що очевидно із табл. 1. 9. Представимо задані функції у ДДНФ і виконаємо послідовно етапи перетворення форм перемикальних функцій.
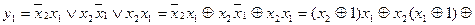
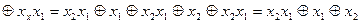 ;
;
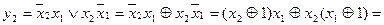
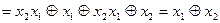 .
.
Деколи трапляється, що перетворення над формулами функцій Буля зручно виконувати у алгебрі Жегалкіна. Зв’язок між алгебра ми Буля та Жегалкіна можна визначити з урахуванням одержаних у прикладі результатів і розглянутих аксіом:
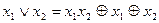 ;
;
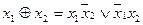 ;
;
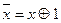 .
.
Відповідно до вигляду полінома Жегалкіна визначається лінійність перемикальної функції.
Функція називається лінійною, якщо її поліном містить кон’юнктивні терми тільки першого рангу. В іншому разі функція вважається нелінійною.
У розглянутому прикладі функція  є нелінійною (її поліном містить терм другого рангу
є нелінійною (її поліном містить терм другого рангу  ), а функція
), а функція  − лінійною.
− лінійною.
1. 5. Функціонально повні системи перемикальних
функцій (базиси функцій).
Проблема функціональної повноти систем перемикальних функцій є однією з найважливіших проблем теорії цифрових автоматів. На практиці для побудови складних логічних схем використовують порівняно невеликий набір логічних елементів, тобто функції від багатьох аргументів подаються за допомогою принципу суперпозиції функціями від меншої кількості аргументів. Отже, системи логічних функцій, за допомогою яких можна аналітично подати будь-яку як завгодно складну перемикальну функцію. Можливість такого перетворення пов’язана з поняттям функціональної повноти систем перемикальних функцій. Знання функціонально повних систем необхідне при розробці комплектів інтегральних мікросхем, за допомогою яких можна побудувати довільний цифровий автомат.
Визначимо, які властивості повинні мати функції, що складають функціонально повні системи.
Будь-яку сукупність функцій можна вважати класом. Розрізняють функціонально замкнені та функціонально повні класи.
Клас функцій є функціонально повним, якщо за допомогою функцій даного класу можна представити методом суперпозиції будь-яку перемикальну функцію від будь-якої кількості аргументів.
Функціонально замкненим називають клас функцій, будь-яка суперпозиція функцій в якому не виводить за межі даного класу.
Серед функціонально замкнутих класів виділяють класи особливого типу, що називаються передповними.
Передповним називають такий клас функцій, додавання до якого будь-якої функції, яка не входить у даний клас, робить клас функцій функціонально повним.
Теорема про функціональну повноту систем функцій базується на приналежності функцій передповним класам.
Існують п’ять передповних класів перемикальних функцій:
− функцій, що зберігають 0 (К0);
− функцій, що зберігають 1 (К1);
− самодвоїстих функцій (КС);
− монотонних функцій (КМ);
− лінійних функцій (КЛ).
Розглянемо пердповні класи докладніше.
До перемикальних функцій класу К0, що зберігають 0, належать усі функції 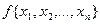 , для яких справедливе співвідношення
, для яких справедливе співвідношення
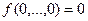 .
.
Іншими словами, це функція, яка на наборі нульових значень її змінних приймає значення 0. Серед елементарних функцій однієї змінної (табл. 1. 3) таких функцій дві: 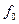 і
і 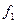 . Серед елементарних функцій двох змінних – вісім: функції
. Серед елементарних функцій двох змінних – вісім: функції 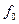 ,
, 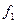 , ...,
, ..., 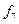 (табл. 1. 4).
(табл. 1. 4).
Оскільки таблиця істинності для функцій, що зберігають 0, у першому рядку значень функції містить 0, то існує рівно 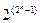 таких функцій.
таких функцій.
До функцій класу К1, що зберігають 1, належать усі функції  , для яких справедливе співвідношення
, для яких справедливе співвідношення
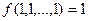 .
.
Прикладами перемикальних функцій, що зберігають 1, є функції однієї змінної 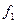 і
і 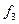 (табл.. 1. 3) і функції двох змінних
(табл.. 1. 3) і функції двох змінних 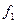 ,
, 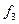 ,
, 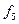 ,
, 
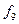 ,
, 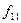 ,
, 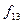 ,
, 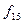 (табл.. 1. 4). Оскільки таблиця істинності для функцій, що зберігають 1, у останньому рядку значень функції містить 1, то існує рівно
(табл.. 1. 4). Оскільки таблиця істинності для функцій, що зберігають 1, у останньому рядку значень функції містить 1, то існує рівно 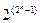 таких функцій.
таких функцій.
Перед тим як ввести поняття класу самодвоїстих функцій, визначимо, які функції називаються двоїстими.
Перемикальні функції 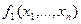 і
і  називаються двоїстими одна одній, якщо виконується співвідношення
називаються двоїстими одна одній, якщо виконується співвідношення
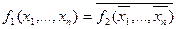 .
.
Наприклад, двоїстими являються функції 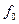 і
і 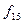 ,
, 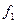 і
і 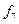 ,
, 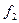 і
і 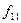 та інші (табл. 1. 4).
та інші (табл. 1. 4).
До самодвоїстих перемикальних функцій належать такі функції, які двоїсті відносно до самих себе, тобто справедливе співвідношення
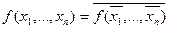 .
.
Якщо домовитися називати протилежними наборами набір (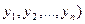 і набір
і набір 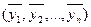 , то можна дати наступне визначення самодвоїстої функції.
, то можна дати наступне визначення самодвоїстої функції.
Булева функція називається самодвоїстою, якщо на будь-яких двох протилежних наборах вона приймає протилежні значення.
Самодвоїстими являються функції 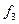 ,
, 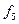 ,
, 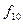 ,
, 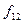 (табл. 1. 4). Із визначення самодвоїстої функції виходить, що вона повністю визначається своїми значеннями на першій половині рядків таблиці істинності. Тому число всіх самодвоїстих булевих функцій дорівнює
(табл. 1. 4). Із визначення самодвоїстої функції виходить, що вона повністю визначається своїми значеннями на першій половині рядків таблиці істинності. Тому число всіх самодвоїстих булевих функцій дорівнює 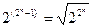 .
.
Перше ніж дати визначення класу КМ монотонних функцій, дамо наступне визначення.
Двійковий набір 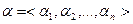 не менший двійкового набору
не менший двійкового набору  , (тобто
, (тобто 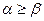 ), якщо для кожної пари (
), якщо для кожної пари (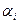 ,
, 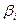 )
) 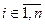 справедливе співвідношення
справедливе співвідношення 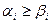 . Такі набори називають порівнянними.
. Такі набори називають порівнянними.
Якщо для двох наборів не виконується ні співвідношення 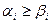 , ні співвідношення
, ні співвідношення 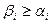 , то набори вважаються непорівнянними. Наприклад набори 1001 і 1000 порівнянні (1001
, то набори вважаються непорівнянними. Наприклад набори 1001 і 1000 порівнянні (1001 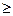 1000). а набори 1001 і 0110 є непорівнянні, так як для них не виконується ні співвідношення
1000). а набори 1001 і 0110 є непорівнянні, так як для них не виконується ні співвідношення 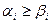 , ні
, ні 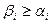 .
.
Функція 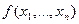 називається монотонною, якщо для двох будь-яких порівнянних наборів
називається монотонною, якщо для двох будь-яких порівнянних наборів 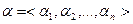 і
і  таких, що
таких, що 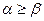 має місце нерівність
має місце нерівність
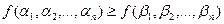 .
.
Монотонними є функції 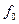 ,
, 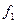 ,
, 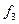 ,
, 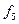 ,
, 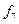 ,
, 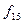 (табл. 1. 4). Функція
(табл. 1. 4). Функція 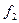 із табл. 1. 4 не монотонна, так як
із табл. 1. 4 не монотонна, так як 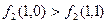 , хоча набір (1, 0) менший, ніж набір (1, 1)
, хоча набір (1, 0) менший, ніж набір (1, 1)
Функція називається лінійною (належить до класу КЛ), якщо є лінійним її поліном Жегалкіна, тобто
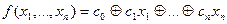 ,
,
де 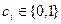 − коефіцієнти.
− коефіцієнти.
Лінійними є перемикальні функції 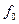 ,
, 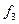 ,
, 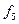 ,
, 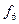 ,
, 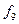 ,
, 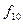 ,
, 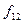 ,
, 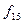 (табл. 1.4), так як
(табл. 1.4), так як
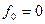 ;
; 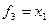 ;
; 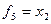 ;
; 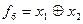 ;
; 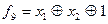 ;
;
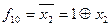 ;
; 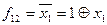 ;
; 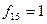 .
.
Оскільки лінійна функція однозначно визначається задаванням коефіцієнтів 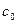 ,
, 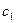 , ...,
, ..., 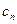 . То число лінійних функцій дорівнює
. То число лінійних функцій дорівнює 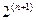 .
.
Теорема Поста-Яблонського.
Для того щоб система перемикальних функцій була функціонально повною, необхідно і достатньо, щоб до її складу входила хоча б одна функція, що не зберігає 0, хоча б одна функція, що не зберігає 1, хоча б одна несамодвоїста функція, хоча б одна нелінійна функція і хоча б одна немонотонна функція.
Іншими словами, система функцій є функціонально повною тоді і тільки тоді, коли вона цілком не міститься в жодному із передповних класів.
Розглянемо приклади функціонально повних систем перемикальних функцій. Для більшої наглядності елементарні функції двох аргументів зведені у табл. 1. 10, в якій показана належність кожної з них передповним класам. У табл. 1. 10 знак „+“ відповідає належності, а знак „−“ − неналежності до відповідного класу.
Таблиця 1. 10
 
| 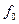
| 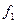
| 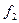
| 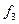
| 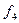
| 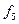
| 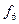
| 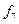
| 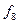
| 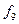
| 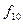
| 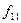
| 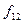
| 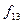
| 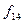
| 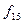
|
| 0 0
0 1
1 0
1 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| К0
| +
| +
| +
| +
| +
| +
| +
| +
| −
| −
| −
| −
| −
| −
| −
| −
|
| К1
| –
| +
| –
| +
| −
| +
| −
| +
| −
| +
| −
| +
| −
| +
| −
| +
|
| КС
| −
| –
| −
| +
| −
| +
| −
| −
| −
| −
| +
| −
| +
| −
| −
| −
|
| КМ
| +
| +
| –
| +
| −
| +
| −
| +
| −
| −
| −
| −
| −
| −
| −
| +
|
| КЛ
| +
| −
| −
| +
| −
| +
| +
| −
| −
| +
| +
| −
| +
| −
| −
| +
|
Ознакою функціональної повноти є, очевидно, наявність знака „−“ в кожному стовпці табл. 1. 10. Усі розглянуті алгебри мають функціонально повні системи перемикальних функцій, що видно із цієї таблиці.
Як приклад, у табл. 1. 11 показано входження функцій булевої алгебри до передповних класів (знак „+“ означає входження, а знак „−“ означає не входження до відповідних класів).
Таблиця 1. 11
|
Функція
| Клас
|
| К0
| К1
| КС
| КМ
| КЛ
|
| І
| +
| +
| −
| +
| −
|
| АБО
| +
| +
| −
| +
| −
|
| НЕ
| −
| −
| +
| −
| +
|
Алгебра Буля має надлишкову систему функцій, що видно з табл. 1. 11. З цієї системи можна вилучити функцію І або функцію АБО. Для забезпечення функціональної повноти достатньо залишити пару функцій: {І, НЕ} чи {АБО, НЕ}. В кожній колонці таблиці при цьому залишиться знак „−“, тобто буде виконана вимога теореми функціональної повноти.
1. 3. 2. Перетворення нормальних форм перемикальних функцій.
Одна і та сама перемикальна функція може задаватися різними аналітичними формами. Необхідність перетворення аналітичних форм функцій може бути обумовлена зміною елементного базису, пошуком форми з мінімальною ціною тощо.
На практиці під час побудови логічних схем можуть використовуватися логічні елементи, що реалізують функції різних алгебр. Найчастіше елементний базис, обумовлений мікроелектронною технологією, містить елементи з множини {І, АБО, НЕ, І-НЕ, АБО-НЕ}, тобто складається з елементів алгебр Буля, Шефера і Пірса. Таку систему функцій можна розглядати в аспекті розширеної практичної алгебри, яка має сукупні властивості відповідних алгебр.
Розширена алгебра має вісім нормальних форм представлення перемикальних функцій, котрі забезпечують побудову дворівневих комбінаційних схем, якщо на кількість входів логічних елементів немає обмежень.
Чотири нормальні форми поширеної алгебри можна одержати виходячи із ДДНФ і ще чотири – виходячи із ДКНФ перемикальної функції або ДДНФ заперечення функції. Якщо немає обмежень на кількість входів логічних елементів, то такі форми перемикальних функцій забезпечують побудову дворівневих комбінаційних схем.
Нормальним формам зручно надати назву, що складається із назв внутрішньої та зовнішньої операції. Наприклад ДДНФ може отримати назву форми І / АБО, ДКНФ – АБО / І і таке інше.
Розглянемо нормальні форми поширеної алгебри перемикальної функції двох аргументів 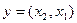 , заданої таблицею істинності (табл. )
, заданої таблицею істинності (табл. )
Таблиця
Таблиця істинності
У формі ДДНФ і ДКНФ задана перемикальна функція має відповідно вигляд:
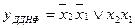 ;
;
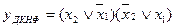 .
.
Виходячи із ДДНФ з урахуванням аксіоми 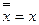 та правила де Моргана (2) одержимо перші чотири нормальні форми:
та правила де Моргана (2) одержимо перші чотири нормальні форми:
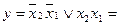 (І / АБО)
(І / АБО)
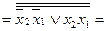
 (І-НЕ / І-НЕ)
(І-НЕ / І-НЕ)
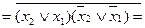 (АБО / І-НЕ)
(АБО / І-НЕ)
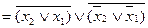 . (АБО-НЕ / АБО)
. (АБО-НЕ / АБО)
На базі ДКНФ аналогічним чином отримаємо ще чотири нормальні форми:
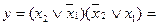 (АБО / І)
(АБО / І)
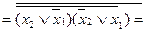
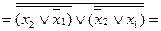 (АБО-НЕ / АБО-НЕ)
(АБО-НЕ / АБО-НЕ)
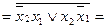 ((І / АБО-НЕ)
((І / АБО-НЕ)
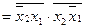 . (І-НЕ / І)
. (І-НЕ / І)
Останні чотири форми можна аналогічно одержати виходячи із заперечення перемикальної функції, що відповідає формі І / АБО-НЕ.
Для отримання заперечення функції виписують із запереченням кон’юнктивні терми наборів, на яких функція дорівнює нулю, поєднані операцією диз’юнкції.
Заперечення даної функції має вигляд:
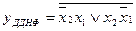 .
.
Послідовно отримаємо:
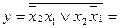 (І / АБО-НЕ)
(І / АБО-НЕ)
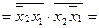 (І-НЕ / І)
(І-НЕ / І)
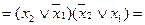 (АБО / І)
(АБО / І)

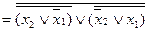 . (АБО-НЕ / АБО-НЕ)
. (АБО-НЕ / АБО-НЕ)
Із числа восьми нормальних форм розширеної алгебри можна знайти ті форми, які дозволяють побудувати комбінаційні схеми з використанням певної підмножини логічних елементів. У результаті дослідження параметрів комбінаційних схем можна обрати з них такі, що відповідають заданій цільовій функції проектування, наприклад, мають мінімальну складність або максимальну швидкодію.
Зауважимо, що отримання нормальних форм не вирішує завдання побудови комбінаційних схем в умовах обмеження кількості входів логічних елементів. У такому випадку необхідно одержати операторні форми функцій.
Розглянемо, яким чином можна перейти від булевого базису {І, АБО, НЕ} до базисів {І, НЕ} та {АБО, НЕ}.
Це питання являється вкрай важливим в разі отримання ДДНФ із заданої таблиці істинності і реалізації перемикальних функцій на інтегральних мікросхемах, оскільки саме мікросхеми дозволяють реалізувати функцію на логічних елементах І-НЕ і АБО-НЕ. При цьому досконалу нормальну форму функції записують у так званій операторній формі, тобто у вигляді суперпозиції операторів заданих логічних елементів.
Оператором логічного елемента називають функцію, що реалізує цей елемент.
В базисі елементів І, АБО, НЕ, І-НЕ, АБО-НЕ таких нормальних форм вісім: І / АБО, І-НЕ / І-НЕ, АБО / І-НЕ, АБО-НЕ / АБО, І / АБО-НЕ,
І-НЕ / І, АБО / І, АБО-НЕ / АБО-НЕ.
При записі цих операторних нормальних форм спочатку записується внутрішня функція а через риску (/) – зовнішня. Наприклад, для ДНФ функції 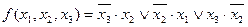 внутрішньою є функція І, а зовнішньою – АБО, тобто нормальна форма даної функції має вигляд: І / АБО.
внутрішньою є функція І, а зовнішньою – АБО, тобто нормальна форма даної функції має вигляд: І / АБО.
Покажемо одержання всіх нормальних форм на прикладі функції
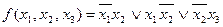 і її заперечення
і її заперечення 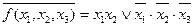 .
.
Нормальні форми будемо позначати з використанням внутрішньої і зовнішньої функцій. Наприклад, у диз’юнктивної нормальної форми (ДНФ) внутрішньою є функція І, а зовнішньою - АБО, тобто ДНФ – форма типу І/АБО.
Взявши подвійне заперечення заданої функції і застосувавши кілька разів правило де Моргана, послідовно одержимо такі нормальні форми:
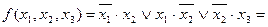 (форма І/АБО);
(форма І/АБО);
= 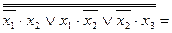
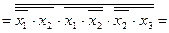
 (форма І-НЕ/І-НЕ)
(форма І-НЕ/І-НЕ)
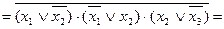 (форма АБО/І-НЕ)
(форма АБО/І-НЕ)
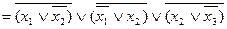 (форма АБО-НЕ/АБО).
(форма АБО-НЕ/АБО).
Виходячи із заперечення заданої функції, запишемо ще чотири нормальні форми:
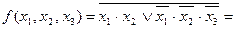 (форма І/АБО-НЕ);
(форма І/АБО-НЕ);
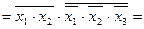 ( форма І-НЕ/І);
( форма І-НЕ/І);
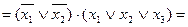 (форма АБО/І);
(форма АБО/І);

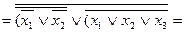 (форма АБО-НЕ/АБО-НЕ).
(форма АБО-НЕ/АБО-НЕ).
Перехід до цих форм запису функції доцільний в разі, коли функція представлена в МДНФ.
2. Комбінаційні схеми
2. 1. Проблема мінімізації перемикальних функцій
Функції 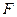 і Ψ, подані у різних формах. Називаються еквівалентними, якщо ці функції приймають однакові значення на всіх наборах аргументів. Тобто їм відповідає одна таблиця істинності.
і Ψ, подані у різних формах. Називаються еквівалентними, якщо ці функції приймають однакові значення на всіх наборах аргументів. Тобто їм відповідає одна таблиця істинності.
Еквівалентні форми перемикальних функцій можуть відрізнятися ціною (кількістю букв у аналітичному записі функції), а комбінаційні схеми, що реалізують еквівалентні форми функцій, можуть відрізнятися складністю.
Метою мінімізації перемикальних функцій є спрощення комбінаційних схем, які реалізують ці перемикальні функції. Проблема мінімізації зводиться до відшукання форми подання функції з мінімальною ціною. Мінімізацію можна виконувати у різних алгебра.
Розглянемо методи мінімізації в диз’юнктивних формах булевої алгебри. Введемо деякі означення.
Перемикальна функція 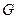 називається імплікантою функції
називається імплікантою функції 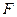 , якщо функція
, якщо функція 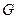 приймає значення одиниці тільки з числа тих наборів, на яких приймає значення одиниці функція
приймає значення одиниці тільки з числа тих наборів, на яких приймає значення одиниці функція 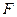 .
.
У загальному випадку імпліканта частково покриває функцію, тобто приймає значення одиниці не на всіх наборах, на котрих функція має значення одиниці. Імпліканта може бути подана кон’юнктивним термом 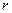 -го ранга, де
-го ранга, де 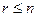 (
(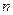 − кількість аргументів функції).
− кількість аргументів функції).
Імпліканта, ніяка частина якої не є імплікантою, називається простою імплікантою.
Диз’юнкція простих імплікант називається скороченою ДНФ (СДНФ).
Сукупність усіх простих імплікант в СДНФ завжди покриває всі одиничні значення функції, але може містити надлишкові (зайві) імпліканти, які повторно покривають функцію на деяких наборах. З метою зменшення ціни форми такі імпліканти можна вилучити із складу СДНФ.
СДНФ без надлишкових імплікант називають тупиковою ДНФ (ТДНФ).
ТДНФ з мінімальною ціною називають мінімальною ДНФ (МДНФ).
Функція може мати декілька ТДНФ і МДНФ.
Таким чином, формальні методи мінімізації функцій зводяться до знаходження МДНФ функції.
Загальну задачу мінімізації булевих функцій можна сформулювати так: знайти аналітичний вираз заданої булевої функції у формі, що містить мінімально можливе число букв. Слід зауважити, що загалом дана задача на разі не розв’язана, однак досить добре досліджена для класу диз’юнктивно-кон’юнктивних форм.
Запис ФАЛ у формі ДДНФ чи ДКНФ, як правило, виявляється неекономічним, що відчувається на етапі структурного синтезу схем.
Покажемо це на прикладі. Хай задана ДДНФ функції
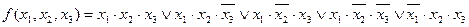
Перетворимо цю ДДНФ, додавши до неї ще один кон’юнктивний член 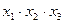 . Це не змінить дану функцію, оскільки
. Це не змінить дану функцію, оскільки 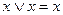 . Тоді отримаємо:
. Тоді отримаємо:
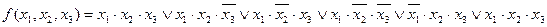 .
.
Користуючись сполучним і розподільним законами для кон’юнкцій і диз’юнкцій, перетворимо даний вираз до вигляду:
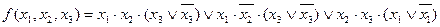
Враховуючи, що 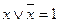 (тобто склеювання по
(тобто склеювання по 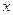 ), одержимо
), одержимо

З прикладу видно, що досконалі нормальні форми для представлення ФАЛ неекономічні. Отже, виникає потреба пошуку найпростішого представлення функцій. Такий пошук полягає у виборі базису логічних елементів і найбільш економного представлення функцій в цьому базисі.
Для уточнення постановки задачі мінімізації булевих функцій дамо низку визначень.
Визначення. Елементарною кон’юнкцією називається кон’юнкція кінцевого числа відмінних між собою булевих змінних, кожна з яких може мати чи ні заперечення.
Визначення. Диз’юнкція елементарних кон’юнкцій називається диз’юнктивною нормальною формою (ДНФ).
Визначення. Мінімальною диз’юнктивною нормальною формою (МДНФ) булевої функції називається ДНФ, яка містить найменше число букв порівняно зі всіма іншими ДНФ, що представляють дану функцію.
Визначення. Булева функція 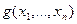 називається імплікантою булевої функції
називається імплікантою булевої функції 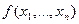 , якщо для будь-якого набору змінних, на якому
, якщо для будь-якого набору змінних, на якому 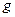 = 1, справедливо
= 1, справедливо  = 1.
= 1.
Приклад. Булева функція  задана табл. 1. 12. Там же наведені всі її імпліканти. При запису функції
задана табл. 1. 12. Там же наведені всі її імпліканти. При запису функції  та її імплікант в ДДНФ маємо:
та її імплікант в ДДНФ маємо:
 ;
;
Таблиця 1. 12
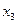  
|   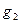 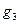  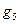 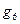 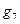
|
| 0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
| 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
1 0 0 0 1 1 1 1
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
1 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1
|
 ;
; 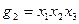 ;
; 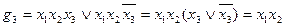 ;
; 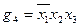 ;
;
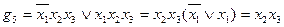 ;
; 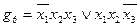 .
.
Визначення. Імпліканта 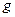 булевої функції
булевої функції  , що є елементарною кон’юнкцією, називається простою, якщо жодна з її (імпліканти
, що є елементарною кон’юнкцією, називається простою, якщо жодна з її (імпліканти 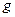 ) частин не являється імплікантою функції
) частин не являється імплікантою функції  .
.
З наведеного прикладу видно, що імпліканти 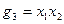 та
та 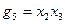 являються простими імплікантами функції
являються простими імплікантами функції  . Імпліканти ж
. Імпліканти ж 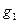 ,
, 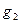 ,
,  ,
, 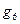 не належать до простих, так як їх частини теж являються імплікантами функції
не належать до простих, так як їх частини теж являються імплікантами функції  . Наприклад,
. Наприклад, 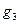 являється частиною
являється частиною 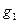 .
.
Наведемо без доказу два твердження, корисні при одержанні мінімальної ДНФ.
1. Диз’юнкція будь-якого числа імплікант булевої функції  також є імплікантою цієї функції.
також є імплікантою цієї функції.
2. Будь-яка булева функція  еквівалентна диз’юнкції всіх своїх простих імплікант. Така форма представлення булевої функції називається скороченою ДНФ.
еквівалентна диз’юнкції всіх своїх простих імплікант. Така форма представлення булевої функції називається скороченою ДНФ.
Перебір всіх можливих імплікант для булевої функції  із розглянутого прикладу дає можливість переконатися, що простих імплікант лише дві:
із розглянутого прикладу дає можливість переконатися, що простих імплікант лише дві: 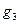 та
та 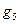 . Отже, скорочена ДНФ функції
. Отже, скорочена ДНФ функції  має вигляд
має вигляд
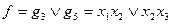 .
.
Із табл. 1. 12 видно, що імпліканти 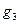 і
і 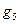 разом покривають своїми одиницями всі одиниці функції
разом покривають своїми одиницями всі одиниці функції  . Одержання скорочених ДНФ являється першим етапом пошуку мінімальних форм булевих функцій. Як вже зазначалось, у скорочену ДНФ входять всі прості імпліканти булевої функції, Інколи із скороченої ДНФ можна вилучити одну або кілька простих імплікант, не порушуючи еквівалентності вихідної функції. Такі прості імпліканти назвемо зайвими. Вилучення зайвих простих імплікант із скорочених ДНФ – другий етап мінімізації.
. Одержання скорочених ДНФ являється першим етапом пошуку мінімальних форм булевих функцій. Як вже зазначалось, у скорочену ДНФ входять всі прості імпліканти булевої функції, Інколи із скороченої ДНФ можна вилучити одну або кілька простих імплікант, не порушуючи еквівалентності вихідної функції. Такі прості імпліканти назвемо зайвими. Вилучення зайвих простих імплікант із скорочених ДНФ – другий етап мінімізації.
Визначення. Скорочена ДНФ булевої функції називається тупиковою, якщо в ній відсутні зайві прості імпліканти.
Усування зайвих простих імплікант із скороченої ДНФ булевої функції не являється однозначним процесом, тобто булева функція може мати кілька тупикових ДНФ.
Твердження. Тупикові ДНФ булевої функції  , що містять мінімальне число букв, являються мінімальними. Мінімальних ДНФ теж може бути декілька.
, що містять мінімальне число букв, являються мінімальними. Мінімальних ДНФ теж може бути декілька.
Аналогічні твердження і визначення можна зробити і для КНФ.
Отже, мінімізація булевих функцій в класі ДДНФ – це пошук мінімальних ДНФ. Цей пошук виконується за два етапи.
На першому етапі за таблицею істинності знаходять ДДНФ заданої функції і одержують тупикові ДНФ.
На другому етапі із одержаних ТДНФ знаходять МДНФ заданої функції. Процес вибору МДНФ неоднозначний, так як для даної функції може існувати декілька тупикових ДНФ і вибір МДНФ здійснюється на основі перебору ТДНФ.
Відомо декілька методів мінімізації булевих функцій. Всі вони практично розрізняються лише на першому етапі – етапі одержання скороченої ДНФ. Варто зауважити, що, нажаль пошук мінімальної ДНФ завжди пов’язаний з деяким перебором рішень. Існують методи зменшення цього перебору, однак він завжди залишається.
Розглянемо найуживаніші із існуючих методи мінімізації булевих функцій: метод Квайна, метод Квайна – Мак-Класкі і графічний метод, так званий метод діаграм Вейча або карт Карно.
1. 6. 2. Метод мінімізації Квайна
Вихідною формою подання перемикальної функції для виконання мінімізації за методом Квайна є ДДНФ.
Метод Квайна базується на використанні співвідношення неповного склеювання
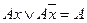 (1. 7)
(1. 7)
і співвідношення поглинання
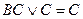 , (1. 8)
, (1. 8)
де  ,
, 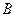 і
і 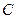 - довільні кон’юнктивні терми;
- довільні кон’юнктивні терми; 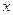 -змінна.
-змінна.
Завдання мінімізації за методом Квайна полягає у знаходженні спрощеної ДНФ шляхом попарного порівняння усіх імплікант, що входять у ДДНФ, з використанням співвідношень неповного склеювання і поглинання. Далі за допомогою таблиці покриття, яка дозволяє позбавитися надлишкових простих імплікант, отримують ядро функції (якщо воно є), а потім знаходять тупикові ДНФ і обирають з них МДНФ.
Під ядром функції розуміють сукупність імплікант, які неможливо вилучити із СДНФ. Такі імпліканти покривають деякі конституенти тільки самостійно.
Мінімізація перемикальної функції виконується за такими етапами.


 ). Наприклад, якщо ДДНФ перемикальної функції має вигляд
). Наприклад, якщо ДДНФ перемикальної функції має вигляд ,
,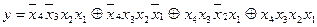 .
.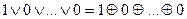 ,
,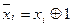 .
.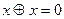 ;
; 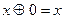 .
.

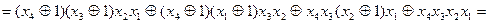

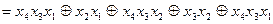 .
. і
і  , заданих таблицею істинності (табл. 1. 9).
, заданих таблицею істинності (табл. 1. 9).

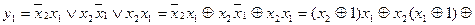
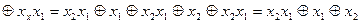 ;
;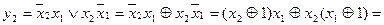
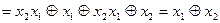 .
.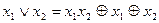 ;
;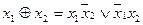 ;
;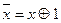 .
. ), а функція
), а функція 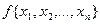 , для яких справедливе співвідношення
, для яких справедливе співвідношення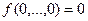 .
.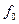 і
і 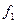 . Серед елементарних функцій двох змінних – вісім: функції
. Серед елементарних функцій двох змінних – вісім: функції 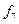 (табл. 1. 4).
(табл. 1. 4).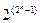 таких функцій.
таких функцій. , для яких справедливе співвідношення
, для яких справедливе співвідношення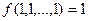 .
.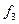 (табл.. 1. 3) і функції двох змінних
(табл.. 1. 3) і функції двох змінних 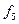 ,
, 
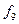 ,
, 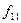 ,
, 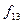 ,
, 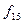 (табл.. 1. 4). Оскільки таблиця істинності для функцій, що зберігають 1, у останньому рядку значень функції містить 1, то існує рівно
(табл.. 1. 4). Оскільки таблиця істинності для функцій, що зберігають 1, у останньому рядку значень функції містить 1, то існує рівно 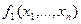 і
і  називаються двоїстими одна одній, якщо виконується співвідношення
називаються двоїстими одна одній, якщо виконується співвідношення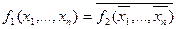 .
.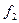 і
і 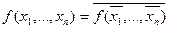 .
.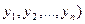 і набір
і набір 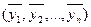 , то можна дати наступне визначення самодвоїстої функції.
, то можна дати наступне визначення самодвоїстої функції.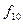 ,
, 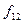 (табл. 1. 4). Із визначення самодвоїстої функції виходить, що вона повністю визначається своїми значеннями на першій половині рядків таблиці істинності. Тому число всіх самодвоїстих булевих функцій дорівнює
(табл. 1. 4). Із визначення самодвоїстої функції виходить, що вона повністю визначається своїми значеннями на першій половині рядків таблиці істинності. Тому число всіх самодвоїстих булевих функцій дорівнює 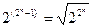 .
.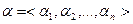 не менший двійкового набору
не менший двійкового набору  , (тобто
, (тобто 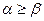 ), якщо для кожної пари (
), якщо для кожної пари (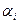 ,
, 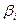 )
) 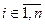 справедливе співвідношення
справедливе співвідношення 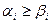 . Такі набори називають порівнянними.
. Такі набори називають порівнянними.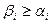 , то набори вважаються непорівнянними. Наприклад набори 1001 і 1000 порівнянні (1001
, то набори вважаються непорівнянними. Наприклад набори 1001 і 1000 порівнянні (1001 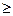 1000). а набори 1001 і 0110 є непорівнянні, так як для них не виконується ні співвідношення
1000). а набори 1001 і 0110 є непорівнянні, так як для них не виконується ні співвідношення 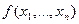 називається монотонною, якщо для двох будь-яких порівнянних наборів
називається монотонною, якщо для двох будь-яких порівнянних наборів 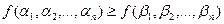 .
.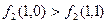 , хоча набір (1, 0) менший, ніж набір (1, 1)
, хоча набір (1, 0) менший, ніж набір (1, 1)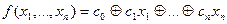 ,
,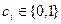 − коефіцієнти.
− коефіцієнти.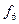 ,
, 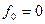 ;
; 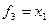 ;
; 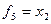 ;
; 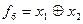 ;
; 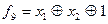 ;
;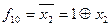 ;
; 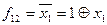 ;
; 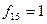 .
.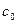 ,
, 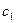 , ...,
, ..., 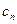 . То число лінійних функцій дорівнює
. То число лінійних функцій дорівнює 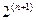 .
.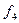
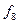
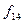
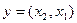 , заданої таблицею істинності (табл. )
, заданої таблицею істинності (табл. )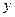
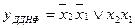 ;
;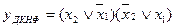 .
.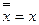 та правила де Моргана (2) одержимо перші чотири нормальні форми:
та правила де Моргана (2) одержимо перші чотири нормальні форми: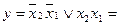 (І / АБО)
(І / АБО)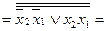
 (І-НЕ / І-НЕ)
(І-НЕ / І-НЕ)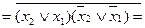 (АБО / І-НЕ)
(АБО / І-НЕ)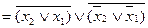 . (АБО-НЕ / АБО)
. (АБО-НЕ / АБО)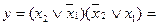 (АБО / І)
(АБО / І)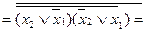
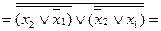 (АБО-НЕ / АБО-НЕ)
(АБО-НЕ / АБО-НЕ)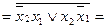 ((І / АБО-НЕ)
((І / АБО-НЕ)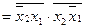 . (І-НЕ / І)
. (І-НЕ / І)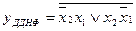 .
.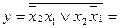 (І / АБО-НЕ)
(І / АБО-НЕ)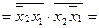 (І-НЕ / І)
(І-НЕ / І)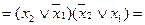 (АБО / І)
(АБО / І)
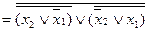 . (АБО-НЕ / АБО-НЕ)
. (АБО-НЕ / АБО-НЕ)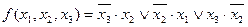 внутрішньою є функція І, а зовнішньою – АБО, тобто нормальна форма даної функції має вигляд: І / АБО.
внутрішньою є функція І, а зовнішньою – АБО, тобто нормальна форма даної функції має вигляд: І / АБО.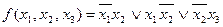 і її заперечення
і її заперечення 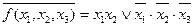 .
.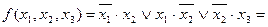 (форма І/АБО);
(форма І/АБО);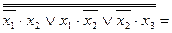
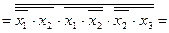
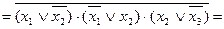 (форма АБО/І-НЕ)
(форма АБО/І-НЕ)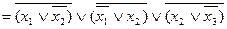 (форма АБО-НЕ/АБО).
(форма АБО-НЕ/АБО).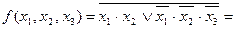 (форма І/АБО-НЕ);
(форма І/АБО-НЕ);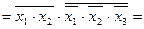 ( форма І-НЕ/І);
( форма І-НЕ/І);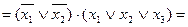 (форма АБО/І);
(форма АБО/І);
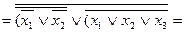 (форма АБО-НЕ/АБО-НЕ).
(форма АБО-НЕ/АБО-НЕ).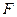 і Ψ, подані у різних формах. Називаються еквівалентними, якщо ці функції приймають однакові значення на всіх наборах аргументів. Тобто їм відповідає одна таблиця істинності.
і Ψ, подані у різних формах. Називаються еквівалентними, якщо ці функції приймають однакові значення на всіх наборах аргументів. Тобто їм відповідає одна таблиця істинності.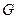 називається імплікантою функції
називається імплікантою функції 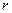 -го ранга, де
-го ранга, де 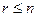 (
(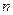 − кількість аргументів функції).
− кількість аргументів функції).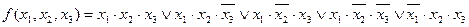
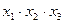 . Це не змінить дану функцію, оскільки
. Це не змінить дану функцію, оскільки 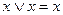 . Тоді отримаємо:
. Тоді отримаємо: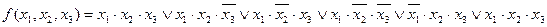 .
.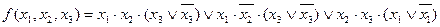
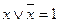 (тобто склеювання по
(тобто склеювання по 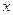 ), одержимо
), одержимо
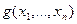 називається імплікантою булевої функції
називається імплікантою булевої функції 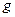 = 1, справедливо
= 1, справедливо  = 1.
= 1. ;
;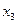

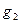
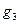

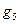
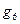
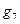
 ;
; 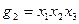 ;
; 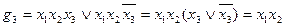 ;
; 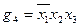 ;
;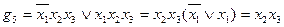 ;
; 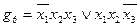 .
.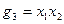 та
та 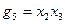 являються простими імплікантами функції
являються простими імплікантами функції 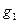 ,
, 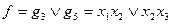 .
.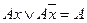 (1. 7)
(1. 7)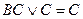 , (1. 8)
, (1. 8) ,
, 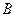 і
і 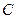 - довільні кон’юнктивні терми;
- довільні кон’юнктивні терми;