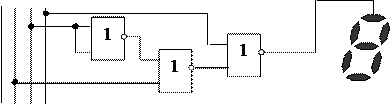Як приклад зробимо синтез схеми комбінаційного цифрового пристрою для керування одним з елементів семисегментного індикатора, який відображує десяткові цифри 0...9. Структурна схема пристрою показана на рис. 1.14.
Рисунок 1.14 – Структурна схема КЦП
1. Таблиця істинності, що завдає алгоритм роботи цього цифрового пристрою наведена в табл. 1.4.
У цієй таблиці у рядках стовпчика Y одиничні значення відповідають відлікам часу у які елемент індикатора є активним (горить), а значення, що дорівнюють 0, відповідають не активному стану елементу. Рядкі у яких стан елементу є не визначенним позначені символом ~ .
2. За даними цієї таблиці запишемо вираз у вигляді досконалої диз’юнктивної нормальної форми (ДДНФ) або у вигляді досконалої кон’юнктивної нормальної форми (ДКНФ). Досконалість логічних функцій передбачає включення у вираз, який отримується, усіх логічних функцій, які
Таблиця 1.4 – Таблиця істинності цифрового пристрю
| №
набору вхідних змінних
|
х3
|
х2
|
х1
|
х0
|
Y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ~
|
|
|
|
|
|
| ~
|
|
|
|
|
|
| ~
|
|
|
|
|
|
| ~
|
|
|
|
|
|
| ~
|
|
|
|
|
|
| ~
|
використовуються для формування логічної функції. Будь-який з цих двох способів однозначно описує алгоритм роботи ЛС.
Для подання у вигляді ДДНФ вибираємо рядки таблиці, на яких значення вихідної функції Y дорівнює L1 (логічній одиниці) і записуємо у вигляді кон’юнкції (логічного добутку) набори вхідних змінних кожного рядка, які об’єднуємо у вигляді диз’юнкції (логічної суми). Математичний вираз, що описує функцію на одному рядку, називається термом. Вхідні змінні повинні входити у кон’юнкцію таким чином, щоб значення логічного добутку дорівнювало L1, для чого вхідні змінні, які мають значення L0 (логічного нуля) необхідно інвертувати. Так, для нульового набору (рядок таблиці з номером 0) кон’юнкція вхідних змінних матиме вигляд:
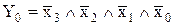
Рядки таблиці, на яких логічна функція не визначена, не беруться до уваги. Тоді логічна функція у вигляді ДДНФ буде записана як
YДДНФ 
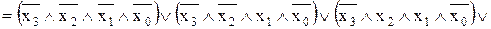
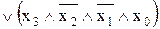 .
.
Для подавання логічної функції у вигляді ДКНФ, вибираємо рядки, на яких значення вихідної функції Y дорівнює логічному нулю L0, і записуємо логічну функцію у вигляді кон’юнкції (логічного добутку) диз’юнкцій вхідних логічних змінних кожного рядка. Для опису вихідної логічної функції Y у вигляді L1 логічні зміні кожного рядка, які входять у вираз ДКНФ, необхідно проінвертувати. ДКНФ логічної функції має вигляд:
YДКНФ 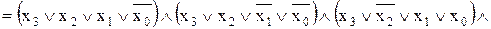
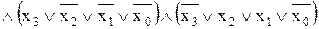 .
.
За виразами ДДНФ і ДКНФ можливо оцінити їхню складність у вигляді коефіцієнта зв’язку Кзв, який визначає кількість елементарних логічних функцій, які необхідно виконати для отримання результатів:
Кзв ДДНФ = 4НІ + 4ТА + 1АБО = 9.
КзвДКНФ = 4НІ + 6АБО + 1ТА = 11.
Таким чином видно, що для реалізації функції у ДДНФ необхідно 9, а для реалізації у ДКНФ – 11 логічних елементів.
3. Мінімізацію досконалих логічних функцій виконуємо за допомогою діаграми Вейча, яка для логічної функції з чотирма вхідними змінними матиме вигляд квадрата 4 × 4 клітинки. Діаграма Вейча для логічної функції, яка описана табл. 1.4, наведена на рис. 1.15.
Для мінімізації логічної функції за одиницями або за нулями на діаграмі Вейча необхідно визначити мінімальну кількість найбільших груп (контурів), що складаються з одиниць або нулів, у вигляді квадратів або прямокутників (об’єднувати можливо лише сусідні клітинки). Сусідніми вважаємо клітинки, що мають спільні сторони, при цьому клітинки, розташовані по горизонтальних та вертикальних сторонах квадрата, є сусідніми. Взагалі, ознакою сусідства можливо вважати відміну двійкового коду номера клітинки лише в одному розряді. Таким чином, аналізуючи номери клітинок у верхньому і нижньому рядках, а також у правому і лівому, можливо зробити висновок, що відповідні клітинки у цих рядках також є сусідніми і діаграму Вейча можна згорнути у циліндр по горизонталі і вертикалі. Кількість клітинок у групі повинна дорівнювати цілому ступеню двійки, тобто 1, 2, 4, 8, 16. На рис. 1.15 у вигляді кругів і овалів показано контури, які об’єднують одиниці і нулі поданої логічної функції. Контури об’єднань можуть будь-яку кількість разів перетинатися, але не можуть повністю суміщатися. Якщо функція має невизначені стани (символ – ~), то функції цієї клітинки можливо надати значення 0 або 1 таким чином, щоб отримати контур, до якого буде входити більша кількість клітинок з однаковими значеннями 0 або 1.
| |
| | 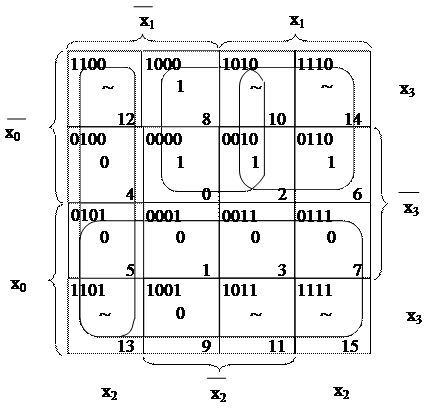 |
Рисунок 1.15 – Діаграма Вейча з контурами для одиниць і нулів
Таким чином, об’єднавши 1 і невизначені стани, отримали два контури, до яких входять клітинки з номерами 0, 2, 8, 10 і 2, 6, 10, 14. Мінімальною формою логічної функції для кожного з контурів будуть координати контурів на діаграмі з відсутніми координатами, на яких функція Y змінює своє значення. Так, координата х1 у контурі з номерами клітинок 0, 2, 8, 10 змінює своє значення; у стовпчику з клітинками 0, 8 вона має значення 0, а у стовпчику з номерами клітинок 2, 10 – 1. Таким чином, координата х1буде відсутня при записуванні мінімальної ДНФ (МДНФ).
Запишемо мінімальні логічні функції, які отримуємо після мінімізації
YМДНФ  ,
,
YМКНФ 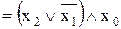 .
.
Оцінимо Кзв для мінімізованих функцій:
для МДНФ Кзв = 2НІ + 2ТА + 1АБО = 5,
для МКНФ Кзв = 1НІ + 1АБО + 1ТА = 3.
4. По одному з отриманих у попередньому пункті виразах МДНФ або МКНФ можемо побудувати схему логічного пристрою у базисі ТА-АБО-НІ. Критерієм вибору є менше значення Кзв або завдання на розробку пристрою.
Логічні схеми будують, як правило, на елементах одного типу в базисах ТА-НІ, АБО-НІ. Це робиться для того, щоб запобігти розкиду параметрів часових затримок у схемі.
Для перетворення виразу до необхідного базису використовується правило подвійної інверсії  та закон де Моргана у такому вигляді:
та закон де Моргана у такому вигляді:
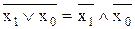
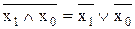
Простіше перетворювати вираз МДНФ до базису ТА-НІ, а вираз МКНФ до базису АБО-НІ, взагалі можливі будь-які перетворення, але при перетворенні МДНФ до базису АБО-НІ і навпаки МКНФ до базису ТА-НІ, схеми будуть більші на один логічний елемент.
Виконаємо перетворення МДНФ у базис ТА-НІ
YМДНФ 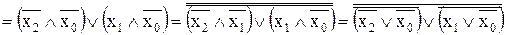 ,
,
і перетворення МКНФ у базис АБО-НІ
YМКНФ 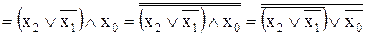 .
.
За цими виразами будується схема дешифратора. На рис. 1.16 схема подана у базисі ТА-НІ, а на рис. 1.17 – у базисі АБО-НІ.

Рисунок 1.16 – Схема дешифратора у базисі ТА-НІ
Рисунок 1.17 – Схема дешифратора у базисі АБО-НІ
Час затримки сигналів розраховується за найдовшим шляхом (за максимальній кількості мікросхем, через які проходить хоча б один з сигналів) і становить
Tзатр = tз.м×Nмc,
де Tзатр – час затримки сигналів схемою;
tз.м – час затримки сигналів однією мікросхемою (визначається
технологією виготовлення мікросхеми);
Nмc – максимальна кількість мікросхем від входу схеми до її виходу.
Для розроблених схем
Tзатр = tз.м×Nмc = 20∙10-6 × 3 = 60∙10-6 с,
де tз.м = 20∙10-6 секунди – часова затримка однієї мікросхеми, вважаючи,
що мікросхема виготовлена за технологією ТТЛ;
Nмc = 3 – кількість мікросхем, через які проходять сигнали х2 і х0 на рис 1.16, а також сигнал х1 на рис. 1.17.




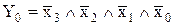

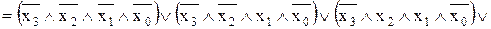
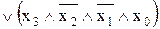 .
.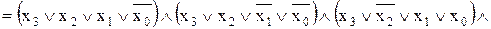
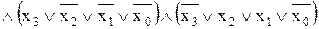 .
.
 ,
,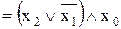 .
. та закон де Моргана у такому вигляді:
та закон де Моргана у такому вигляді: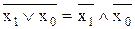
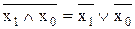
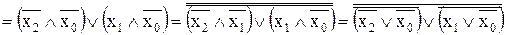 ,
,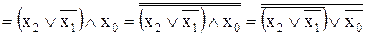 .
.