Дослідити згасаючі коливання фізичного маятника і за виміряним числом повних коливань Nt і часу релаксації t обчислити:
· сталу згасання g,
· коефіцієнт опору r,
· логарифмічний декремент згасання l ,
· добротність коливальної системи Q,
оцінити коефіцієнт тертя кочення.
Теоретичні відомості:
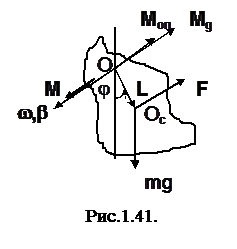 Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор
Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор 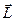 . Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту
. Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту 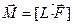 зовнішніх сил
зовнішніх сил 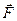 , моменту сили тяжіння
, моменту сили тяжіння 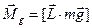 та моменту сил опору
та моменту сил опору 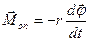 , де
, де 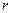 ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj.
¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj.
Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:
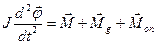 , (1.41)
, (1.41)
де J ¾ момент інерції тіла. Вектори  лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:
лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:
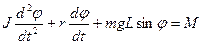 . (2.41)
. (2.41)
В канонічному вигляді рівняння (2.41) можна записати так
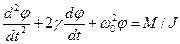 , (3.41)
, (3.41)
де 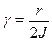 ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань, 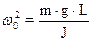 , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p  , де lпр =
, де lпр = 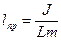 ¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)
¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)
Розв'язок (3.41) шукаємо підстановкою Ейлера j=elt.
Знайдемо перші дві похідні від j по часу
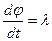 elt,
elt,  = l2elt. (4.41)
= l2elt. (4.41)
Підставляючи похідні (4.41) в (3.41), одержимо:
elt ( l2 + 2gl + w02 ) = 0. (5.41)
Квадратне рівняння l2 + 2gl + w02 = 0 в (5.41) називається характеристичним. Його розв'язок
 ,
, 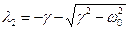 (6.41)
(6.41)
дає два фундаментальні розв'язки диференціального рівняння
j1 = exp(l1t), j2 = exp(l2t), (7.41)
з яких утворюється загальний розв'язок. Загальним розв'язком однорідного рівняння (3.41) буде лінійна комбінація фундаментальних розв'язків
j = Аexp(l1t) + Bexp(l2t) (8.41)
з дійсними коефіцієнтами А, В.
Якісно розрізняють два випадки руху маятника:
1) При g > w0 ¾ аперіодичний рух. При цьому l1,l2 < 0 ¾ дійсні числа. Функція j є спадною функцією часу (l1,l2<0) і описує асимптотичне, в експоненційній залежності від часу, повернення маятника в стан рівноваги. При цьому коливальний рух не здійснюється.
2) Якщо g < w0, маятник буде здійснювати коливальний рух. При цьому
l1 = - g+іw, l2 = - g-іw, (9.41)
де і =  ¾ уявна одиниця, w =
¾ уявна одиниця, w = 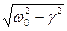 ¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:
¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:
j = e-gt(Aeiwt + Be-iwt) (10.41)
з комплексними коефіцієнтами А, В. Для знаходження величин А та В зауважимо, що функція j є дійсною функцією часу, і за цим вона має дорівнювати своїй комплексно спряженій функції j = j* Þ
e-gt(Aeiwt+Be-iwt) = e-gt(A*e-iwt +B*eiwt). (11.41)
Прирівнюючи в (11.41) коефіцієнти при однакових експонентах, одержимо В=А*. Для зручності комплексну сталу А візьмемо в експоненціальному вигляді
А = а0eia/2, де а0 ¾ дійсна величина. Тепер
j = а0/2·e-gt (ei(wt+a) +e-i(wt+a)) (12.41)
і, користуючись формулою Ейлера e±ix = cosx ± i×sinx, вираз в дужках запишемо у вигляді:
j = 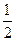 а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ
а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ
j = j0(t)×cos(wt+a). (13.41)
В (13.41) j0(t) = a0e-gt ¾ амплітуда коливань ¾ спадна функція часу, Ф = wt+a ¾ фаза коливань, Ф0 = a ¾ початкова фаза.


 Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор
Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор 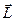 . Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту
. Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту 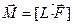 зовнішніх сил
зовнішніх сил 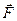 , моменту сили тяжіння
, моменту сили тяжіння 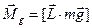 та моменту сил опору
та моменту сил опору 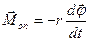 , де
, де 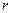 ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj.
¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj. 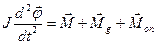 , (1.41)
, (1.41) лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:
лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі: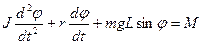 . (2.41)
. (2.41)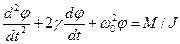 , (3.41)
, (3.41)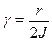 ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань, 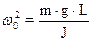 , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p  , де lпр =
, де lпр = 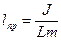 ¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)
¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)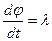 elt,
elt,  = l2elt. (4.41)
= l2elt. (4.41) ,
, 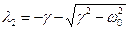 (6.41)
(6.41) ¾ уявна одиниця, w =
¾ уявна одиниця, w = 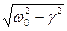 ¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:
¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд: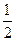 а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ
а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ