Носій реляційної алгебри є множина відношень, сигнатура, крім уведених операцій (об'єднання, перетинання, різниці, розширеного декартова добутку), включає спеціальні операції над відношеннями: вибір, проекція й з'єднання.
Відповідно до потреб практики вводяться й інші операції: обмін позиціями; подвоєння позицій; згортка, композиція.
Визначення 3.8. Операція вибору являє собою процедуру побудови “горизонтальної” підмножини відношень, тобто підмножини кортежів, що мають задану властивість.
Для визначення проекції відношення множина у реляційній алгебрі розбивається на дві підмножини у випадку бінарного відношення або на 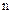 підмножин у випадку
підмножин у випадку 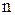 -арного:
-арного:
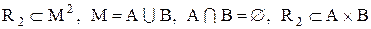 ;
;
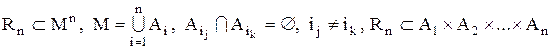 .
.
Визначення 3.9.Проекцією  бінарного відношення на множину
бінарного відношення на множину 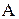 називається сукупність елементів
називається сукупність елементів 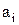 , розташованих в упорядкованих парах на перших позиціях:
, розташованих в упорядкованих парах на перших позиціях:
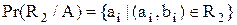 . (3.10)
. (3.10)
Проекція за одним доменом визначає сукупність елементів і не є відношенням.
Визначення 3.10.Проекцією 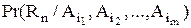
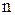 -арного відношення на множини
-арного відношення на множини  (
( 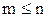 ) називається сукупність кортежів
) називається сукупність кортежів 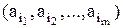 , де
, де 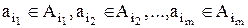 , кожний з яких є частиною елемента
, кожний з яких є частиною елемента 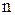 -арного відношення
-арного відношення  :
:
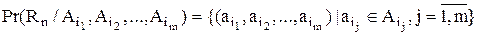 . (3.11)
. (3.11)
Операція проекції визначає побудову “вертикальної” підмножини відношення, тобто сукупності котрежей, що здобуваються вибором одних і виключенням інших доменів.
Проекція за двома та більш доменами є відношенням ступеня 2 та більше залежно від кількості стовпців, за якими ведеться проектування.
Визначення 3.11. Операція з'єднання за двома таблицями, що має спільний домен, дозволяє побудувати одну таблицю, кожний рядок якої утворюється з'єднанням двох рядків вихідних таблиць. Із заданих таблиць беруть рядки, що містять ті самі значення із загального домену; якому зіставляється один стовпець.
Запит у реляційній базі даних буде виконаний тим швидше, чим менше операцій над відношеннями він містить.
Приклад 3.5.Для відношення 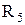 у формі (3.9) визначити результати виконання наступних операцій:
у формі (3.9) визначити результати виконання наступних операцій:  – вибір за доменом
– вибір за доменом 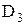 при значенні
при значенні  ;
;  – проекція за доменом
– проекція за доменом 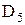 ;
; 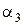 – проекція за двома доменами
– проекція за двома доменами 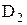 ,
, 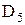 ;
; 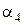 – з'єднання за доменом D1за умовою «дорівнює», для двох таблиць
– з'єднання за доменом D1за умовою «дорівнює», для двох таблиць  (перші чотири кортежі
(перші чотири кортежі 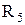 ) і
) і 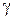 (другі чотири кортежі
(другі чотири кортежі 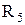 ).
).
Розв’язок. Відповідно до визначення 3.8, результат вибору за доменом 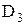 являє собою відношення ступеня 5, що складається з векторів, у яких на 3-й позиції розташовується координата
являє собою відношення ступеня 5, що складається з векторів, у яких на 3-й позиції розташовується координата 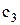 :
:
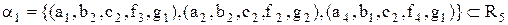 .
.
Результат проектування відношення 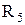 за доменом
за доменом 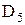 відповідно до визначення 3.9 є сукупність елементів, з яких складається стовпець
відповідно до визначення 3.9 є сукупність елементів, з яких складається стовпець 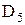 :
:  .
.
Результат проектування відношення 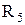 за доменами
за доменами 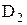 ,
, 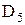 відповідно до визначення 3.10 є сукупність упорядкованих пар:
відповідно до визначення 3.10 є сукупність упорядкованих пар:

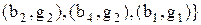 .
.
Згідно з визначенням 3.11, результат виконання операції з'єднання за доменом  за умови рівності для двох таблиць
за умови рівності для двох таблиць 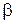 (перші чотири кортежі
(перші чотири кортежі 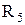 ) і
) і 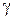 (другі чотири кортежі
(другі чотири кортежі 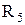 ) являє собою сукупність векторів, утворених послідовною конкатенацією векторів із двох зазначених підтаблиць
) являє собою сукупність векторів, утворених послідовною конкатенацією векторів із двох зазначених підтаблиць 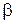 і
і 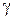 :
:
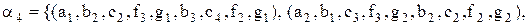
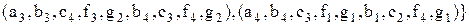 .
.
Результати дії операцій  є відношеннями, тобто не виводять із множини відношень. Результат дії операції проекції за доменом
є відношеннями, тобто не виводять із множини відношень. Результат дії операції проекції за доменом 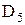 не є відношенням, тобто застосування даної операції виводить із множини відношень.
не є відношенням, тобто застосування даної операції виводить із множини відношень.
3.4 Контрольні питання
1. Що називається 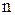 -місцевим відношенням?
-місцевим відношенням?
2. Які відношення називаються сумісними?
3. Які існують операції над відношеннями?
4. Що являє собою реляційна алгебра?
5. Для чого призначена алгебра відношень?
6. Для яких операцій над відношеннями умова сумісності є обов'язковою?
7. Для яких операцій над відношеннями умова сумісності не є обов'язковою?
8. Які існують спеціальні операції над відношеннями?
9. З яких елементів складаються відношення?
10. Як визначається об'єднання відношень?
11. Як визначається перетинання відношень?
12. Як визначається різниця відношень?
13. Що являє собою розширений декартів добуток відношень?
14. Як визначається конкатенація векторів?
15. Чому дорівнює потужність розширеного декартова добутку відношень?
16. Як визначається операція вибору?
17. Як визначається проекція відношення за доменом?
18. Як визначається проекція відношення за декількома доменами?
19. Як визначається операція з'єднання?
20. Чому дорівнює ступінь розширеного декартова добутку відношень?
4 Бінарні відношення
Бінарні (або двомісні) відношення часто застосовуються на практиці та є добре вивченими.
Визначення 4.1.Бінарним відношенням 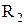 на множині
на множині  називається підмножина декартова квадрата множини
називається підмножина декартова квадрата множини  :
:  .
.
4.1 Способи завдання бінарних відношень
Бінарні відношення можна задати такими способами.
Спосіб 1. Перерахування елементів, якими утворене відношення. Як елементи бінарного відношення виступають упорядковані пари.
Приклад 4.1.Бінарне відношення на множині 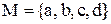 задано перерахуванням упорядкованих пар:
задано перерахуванням упорядкованих пар: 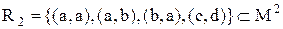 .
.
Спосіб 2. Матриця суміжності.
Визначення 4.2.Матриця суміжності 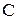 бінарного відношення
бінарного відношення 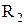 на множині
на множині 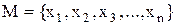 – це квадратна таблиця розміру
– це квадратна таблиця розміру 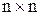 (
( 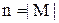 – потужність множини, на якому задане бінарне відношення), де елемент
– потужність множини, на якому задане бінарне відношення), де елемент 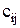 , що розташований на перетинанні
, що розташований на перетинанні  -го рядка та
-го рядка та 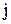 -го стовпця, визначається таким чином:
-го стовпця, визначається таким чином:
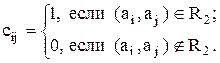 (4.1)
(4.1)
Отже, кожна комірка 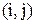 взаємно однозначно відповідає елементам декартова квадрата. Комірку
взаємно однозначно відповідає елементам декартова квадрата. Комірку 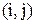 , що відповідає елементу, який належить відношенню
, що відповідає елементу, який належить відношенню  , відзначають одиницею, в інші клітки поміщають нулі.
, відзначають одиницею, в інші клітки поміщають нулі.
Приклад 4.2. Дана множина 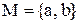 та її декартів квадрат:
та її декартів квадрат:  . На множині
. На множині  розглядається бінарне відношення
розглядається бінарне відношення 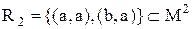 . Матриця суміжності бінарного відношення має вигляд:
. Матриця суміжності бінарного відношення має вигляд:
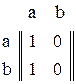 .
.
Спосіб 3. Граф. Бінарне відношення можна задати за допомогою графової діаграми.
Визначення 4.3. Граф – це сукупність множини  із заданим на ньому бінарному відношенні
із заданим на ньому бінарному відношенні 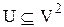 :
:  , де
, де  – носій графа (сукупність вершин),
– носій графа (сукупність вершин), 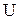 – сигнатура графа (сукупність дуг).
– сигнатура графа (сукупність дуг).
Сигнатура встановлює зв'язок між вершинами графа. Графом також називається і графова діаграма, якою він зображується: вершини позначаються крапками, упорядковані пари вершин – дугами, де дуга спрямована з вершини, що розташована на першій позиції в упорядкованій парі, у вершину, яка розташована на другій позиції.
Приклад 4.3. Граф бінарного відношення 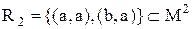 , заданого на множині
, заданого на множині 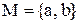 (див. приклад 4.2) має вигляд (рис. 4.1):
(див. приклад 4.2) має вигляд (рис. 4.1):
Рис. 4.1. Граф бінарного відношення із приклада 4.3
Розглянемо наступний приклад, що ілюструє інформаційний обмін між пристроями ЕОМ, блок-схема якої вперше була запропонована Джоном фон Нейманом.
Приклад 4.3.Дана множина 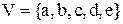 . Тут
. Тут 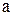 – пристрій уведення;
– пристрій уведення;  – процесор (арифметичний пристрій);
– процесор (арифметичний пристрій); 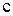 – пристрій керування;
– пристрій керування; 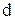 – запам'ятовувальний пристрій;
– запам'ятовувальний пристрій; 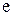 – пристрій виведення. Відношення
– пристрій виведення. Відношення  на множині
на множині  :
:

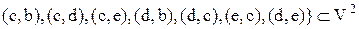 . (4.2)
. (4.2)
можна задати за допомогою графа (рис. 4.2):
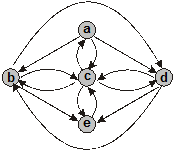
Рис. 4.2. Інформаційний обмін між пристроями ЕОМ
Спосіб 4. Фактор-множина
Визначення 4.4. Околиця одиничного радіуса елемента  – це сукупність елементів
– це сукупність елементів 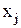 таких, що
таких, що 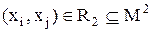 :
:
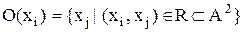 . (4.3)
. (4.3)
Визначення 4.5.Фактор-множиною 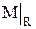 (
( 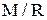 або
або 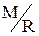 ) множини
) множини  за бінарним відношенням R називається сукупність околиць одиничного радіуса для всіх елементів множини
за бінарним відношенням R називається сукупність околиць одиничного радіуса для всіх елементів множини  при заданому на ньому бінарному відношенні
при заданому на ньому бінарному відношенні 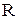 :
:
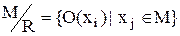 . (4.4)
. (4.4)
Приклад 4.4.Для бінарного відношення (4.2) із приклада 4.3 фактор-множина зображується наступним чином:
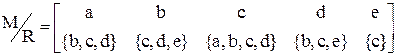 ,
,
де у верхньому рядку розташовані елементи множини  , на якому задане бінарне відношення, у нижньому – околиці одиничного радіуса відповідних елементів.
, на якому задане бінарне відношення, у нижньому – околиці одиничного радіуса відповідних елементів.
4.2 Властивості бінарних відношень
Бінарні відношення мають три основні властивості, згідно до яких вони класифікуються: рефлексивність, симетричність, транзитивність.
Визначення 4.6. Бінарне відношення 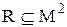 є рефлексивним, якщо виконується умова:
є рефлексивним, якщо виконується умова:
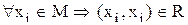 , (4.5)
, (4.5)
тобто для будь-якого елемента  з множини
з множини  кожна впорядкована пара вигляду
кожна впорядкована пара вигляду 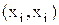 належить бінарному відношенню.
належить бінарному відношенню.
У матриці рефлексивного бінарного відношення 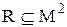 на головній діагоналі розташовані одиниці:
на головній діагоналі розташовані одиниці:
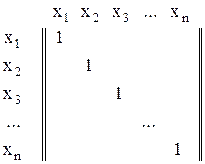 , (4.6)
, (4.6)
у графі – всі вершини мають петлі (рис. 4.3):
Рис. 4.3. Петля в графі рефлексивного бінарного відношення
Визначення 4.7. Бінарне відношення 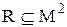 є симетричним, якщо виконується умова:
є симетричним, якщо виконується умова:
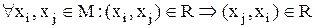 , (4.7)
, (4.7)
тобто для будь-яких елементів  ,
, 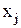 з множини
з множини  таких, що впорядкована пара
таких, що впорядкована пара 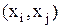 належить бінарному відношенню
належить бінарному відношенню 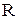 , симетрична пара
, симетрична пара 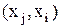 також належить даному відношенню.
також належить даному відношенню.
Матриця симетричного бінарного відношення симетрична відносно головної діагоналі:
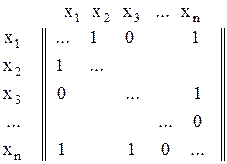 . (4.8)
. (4.8)
У графі симетричного бінарного відношення – наявність між кожною парою вершин, що перебувають у відношенні 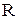 ,двох протилежно спрямованих дуг (рис. 4.4):
,двох протилежно спрямованих дуг (рис. 4.4):

Рис. 4.4. Симетрично спрямовані дуги
Приклад 4.5. Видалення в графі із приклада 4.3 (див. рис. 4.2) дуг 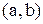 ,
, 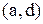 ,
, 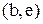 ,
, 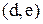 приводить до симетричного відношення
приводить до симетричного відношення 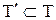 (рис. 4.5).
(рис. 4.5).
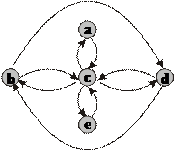
Рис. 4.5. Симетричне бінарне відношення
Визначення 4.8. Бінарне відношення 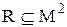 називається транзитивним, якщо виконано властивість:
називається транзитивним, якщо виконано властивість:
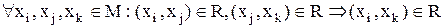 , (4.9)
, (4.9)
для будь-яких трьох елементів 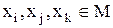 таких, що послідовно утворені впорядковані пари із цих елементів
таких, що послідовно утворені впорядковані пари із цих елементів 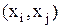 ,
,  перебувають у відношенні
перебувають у відношенні 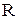 , тоді пари із крайніх елементів
, тоді пари із крайніх елементів 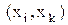 також належить даному відношенню.
також належить даному відношенню.
Граф транзитивного бінарного відношення характеризується наявністю транзитивно замикаючих дуг (рис. 4.6) для кожних двох пар з умови (посилки) даної властивості (4.9).
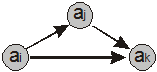
Рис. 4.6. Транзитивно замикаюча дуга 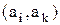
Приклад 4.6. У графі на рис. 4.5 транзитивно замикаючими є наступні дуги: для впорядкованих пар 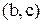 ,
, 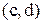 –
– 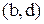 ; для пар
; для пар 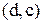 ,
, 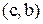 –
–  ; для пар
; для пар 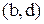 ,
, 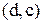 –
– 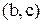 ; для
; для  ,
, 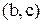 –
– 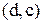 .
.
Уводяться також додаткові властивості, засновані на наведених вище:
– антирефлексивність (у матриці суміжності на головній діагоналі всі елементи нульові, у графі не існує петель): 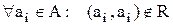 ;
;
– нерефлексивність (у матриці суміжності по головній діагоналі розташовані як нулі, так і одиниці, у графі деякі вершини мають петлі): 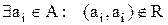 ;
;
– антисиметричність (всі відповідні симетричні комірки матриці суміжності різні; у графі немає жодної пари симетрично спрямованих дуг): 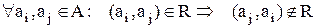 ;
;
– несиметричність (якщо умова симетричності порушується хоча б для однієї пари, тобто 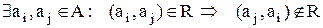 ;
;
– нетранзитивність: якщо 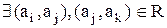 , для яких не виконується умова транзитивності, тобто
, для яких не виконується умова транзитивності, тобто  .
.
Приклад 4.7. Після видалення симетричних і транзитивно замикаючих дуг у графі із приклада 4.3 (див. рис. 4.2), тобто всіх дуг, крім  , відношення
, відношення  стає антисиметричним, антирефлексивним, не транзитивним (рис. 4.7):
стає антисиметричним, антирефлексивним, не транзитивним (рис. 4.7):
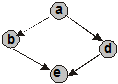
Рис. 4.7. Антирефлексивне, антисиметричне, нетранзитивне відношення
4.3 Бінарне відношення еквівалентності
Відношення еквівалентності – спеціальний тип бінарного відношення, затребуваний на практиці.
Визначення 4.9. Бінарним відношенням еквівалентності 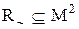 називається рефлексивне, симетричне й транзитивне відношення, тобто
називається рефлексивне, симетричне й транзитивне відношення, тобто 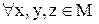 :
:
1) рефлексивність означає, що кожний елемент еквівалентний сам собі: 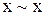 ;
;
2) симетричність означає, що якщо елемент 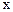 еквівалентний елементу
еквівалентний елементу 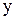 , то й
, то й 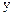 еквівалентний елементу
еквівалентний елементу 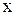 :
: 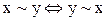 ;
;
3) транзитивність: якщо елемент 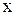 еквівалентний елементу
еквівалентний елементу 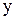 , а
, а 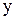 еквівалентний елементу
еквівалентний елементу 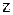 , то
, то 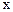 еквівалентний
еквівалентний 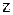 :
: 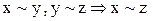 .
.
Відношення еквівалентності ілюструється графом з петлями й симетрично спрямованими дугами, які попарно мають транзитивно замикаючі дуги (рис. 4.8).
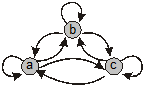
Рис. 4.8. Граф бінарного відношення еквівалентності
Приклад 4.8. Бінарне відношення еквівалентності ілюструє роботу тригера, граф переходів якого зображений на рис. 4.10.

а б
Рис. 4.9. Граф переходів (а) і структура тригера (б)
Визначення 4.10.Клас еквівалентності 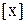 елемента
елемента 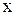 є множина всіх елементів
є множина всіх елементів 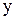 , кожний з яких перебуває з елементом
, кожний з яких перебуває з елементом 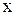 увідношенні еквівалентності:
увідношенні еквівалентності:
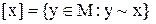 або
або 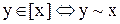 . (4.10)
. (4.10)
Визначення 4.11.Розбивкою множини  називається сімейство непустих попарно непересічних підмножин (класів), об'єднання яких співпадає з
називається сімейство непустих попарно непересічних підмножин (класів), об'єднання яких співпадає з  , тобто зображення множини
, тобто зображення множини  у вигляді попарно непересічних підмножин називається розбивкою множини
у вигляді попарно непересічних підмножин називається розбивкою множини  . Індекс розбивки визначається його потужністю.
. Індекс розбивки визначається його потужністю.
Нехай 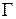 – сімейство підмножин множини
– сімейство підмножин множини  :
: 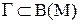 . Відповідно до визначення 4.11,
. Відповідно до визначення 4.11, 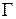 є розбивкою множини
є розбивкою множини  , якщо воно задовольняє властивостям:
, якщо воно задовольняє властивостям:
1) Будь-яка множина  із
із 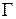 не є порожньою, тобто
не є порожньою, тобто 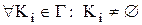 ;
;
2) Довільні дві множини з розбивки 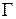 не мають спільних елементів:
не мають спільних елементів:
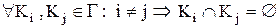 ;
;
3) Об'єднання всіх множин із 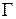 співпадає з множиною
співпадає з множиною  :
:
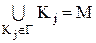 .
.
Приклад 4.9. Розбивками триелементної множини 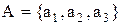 є:
є:
 – сама велика (максимальна) розбивка індексу одиниця, що містить одну єдину непусту множину, яка співпадає з множиною
– сама велика (максимальна) розбивка індексу одиниця, що містить одну єдину непусту множину, яка співпадає з множиною 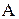 ;
;
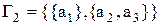 ;
; 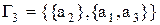 ;
; 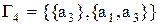 – розбивки індексу 2;
– розбивки індексу 2;


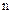 підмножин у випадку
підмножин у випадку 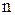 -арного:
-арного: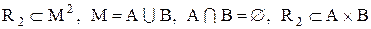 ;
;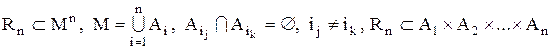 .
. бінарного відношення на множину
бінарного відношення на множину 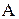 називається сукупність елементів
називається сукупність елементів 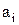 , розташованих в упорядкованих парах на перших позиціях:
, розташованих в упорядкованих парах на перших позиціях: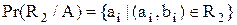 . (3.10)
. (3.10)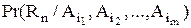
 (
( 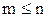 ) називається сукупність кортежів
) називається сукупність кортежів 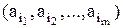 , де
, де 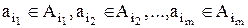 , кожний з яких є частиною елемента
, кожний з яких є частиною елемента  :
: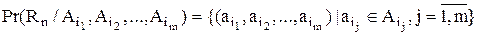 . (3.11)
. (3.11)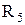 у формі (3.9) визначити результати виконання наступних операцій:
у формі (3.9) визначити результати виконання наступних операцій:  – вибір за доменом
– вибір за доменом 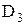 при значенні
при значенні  ;
;  – проекція за доменом
– проекція за доменом 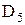 ;
; 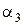 – проекція за двома доменами
– проекція за двома доменами 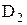 ,
, 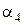 – з'єднання за доменом D1за умовою «дорівнює», для двох таблиць
– з'єднання за доменом D1за умовою «дорівнює», для двох таблиць  (перші чотири кортежі
(перші чотири кортежі 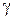 (другі чотири кортежі
(другі чотири кортежі 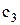 :
: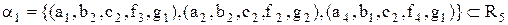 .
. .
.
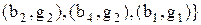 .
. за умови рівності для двох таблиць
за умови рівності для двох таблиць 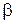 (перші чотири кортежі
(перші чотири кортежі 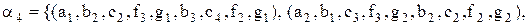
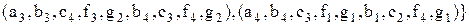 .
. є відношеннями, тобто не виводять із множини відношень. Результат дії операції проекції за доменом
є відношеннями, тобто не виводять із множини відношень. Результат дії операції проекції за доменом 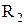 на множині
на множині  називається підмножина декартова квадрата множини
називається підмножина декартова квадрата множини  .
.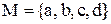 задано перерахуванням упорядкованих пар:
задано перерахуванням упорядкованих пар: 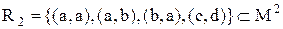 .
.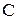 бінарного відношення
бінарного відношення 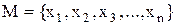 – це квадратна таблиця розміру
– це квадратна таблиця розміру 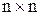 (
( 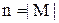 – потужність множини, на якому задане бінарне відношення), де елемент
– потужність множини, на якому задане бінарне відношення), де елемент 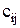 , що розташований на перетинанні
, що розташований на перетинанні  -го рядка та
-го рядка та 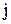 -го стовпця, визначається таким чином:
-го стовпця, визначається таким чином: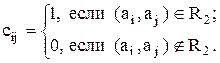 (4.1)
(4.1)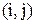 взаємно однозначно відповідає елементам декартова квадрата. Комірку
взаємно однозначно відповідає елементам декартова квадрата. Комірку 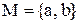 та її декартів квадрат:
та її декартів квадрат:  . На множині
. На множині  розглядається бінарне відношення
розглядається бінарне відношення 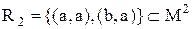 . Матриця суміжності бінарного відношення має вигляд:
. Матриця суміжності бінарного відношення має вигляд: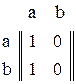 .
. із заданим на ньому бінарному відношенні
із заданим на ньому бінарному відношенні 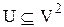 :
:  , де
, де 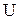 – сигнатура графа (сукупність дуг).
– сигнатура графа (сукупність дуг).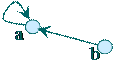
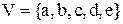 . Тут
. Тут 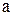 – пристрій уведення;
– пристрій уведення;  – процесор (арифметичний пристрій);
– процесор (арифметичний пристрій); 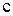 – пристрій керування;
– пристрій керування; 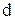 – запам'ятовувальний пристрій;
– запам'ятовувальний пристрій; 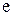 – пристрій виведення. Відношення
– пристрій виведення. Відношення  на множині
на множині 
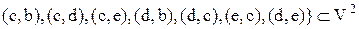 . (4.2)
. (4.2)
 – це сукупність елементів
– це сукупність елементів 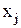 таких, що
таких, що 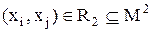 :
: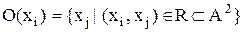 . (4.3)
. (4.3)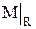 (
( 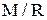 або
або 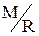 ) множини
) множини 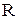 :
: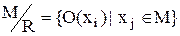 . (4.4)
. (4.4)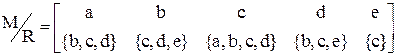 ,
,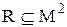 є рефлексивним, якщо виконується умова:
є рефлексивним, якщо виконується умова: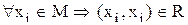 , (4.5)
, (4.5)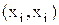 належить бінарному відношенню.
належить бінарному відношенню.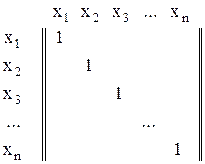 , (4.6)
, (4.6)
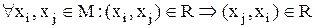 , (4.7)
, (4.7)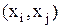 належить бінарному відношенню
належить бінарному відношенню 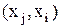 також належить даному відношенню.
також належить даному відношенню.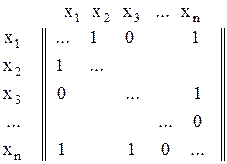 . (4.8)
. (4.8)
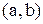 ,
, 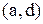 ,
, 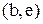 ,
, 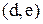 приводить до симетричного відношення
приводить до симетричного відношення 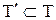 (рис. 4.5).
(рис. 4.5).
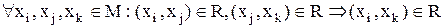 , (4.9)
, (4.9)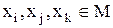 таких, що послідовно утворені впорядковані пари із цих елементів
таких, що послідовно утворені впорядковані пари із цих елементів  перебувають у відношенні
перебувають у відношенні 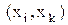 також належить даному відношенню.
також належить даному відношенню.
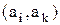
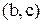 ,
, 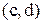 –
– 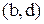 ; для пар
; для пар 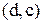 ,
, 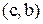 –
–  ; для пар
; для пар 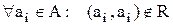 ;
;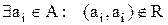 ;
;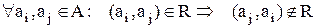 ;
;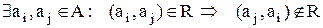 ;
;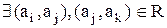 , для яких не виконується умова транзитивності, тобто
, для яких не виконується умова транзитивності, тобто  .
. , відношення
, відношення 
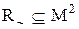 називається рефлексивне, симетричне й транзитивне відношення, тобто
називається рефлексивне, симетричне й транзитивне відношення, тобто 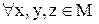 :
: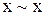 ;
;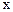 еквівалентний елементу
еквівалентний елементу 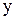 , то й
, то й 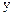 еквівалентний елементу
еквівалентний елементу 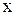 :
: 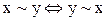 ;
;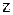 , то
, то 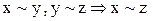 .
.

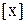 елемента
елемента 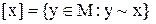 або
або 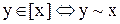 . (4.10)
. (4.10)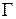 – сімейство підмножин множини
– сімейство підмножин множини 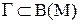 . Відповідно до визначення 4.11,
. Відповідно до визначення 4.11,  із
із 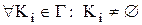 ;
;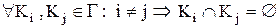 ;
;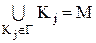 .
.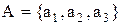 є:
є: – сама велика (максимальна) розбивка індексу одиниця, що містить одну єдину непусту множину, яка співпадає з множиною
– сама велика (максимальна) розбивка індексу одиниця, що містить одну єдину непусту множину, яка співпадає з множиною 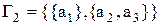 ;
; 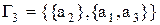 ;
; 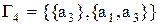 – розбивки індексу 2;
– розбивки індексу 2;